机器学习笔记之优化算法(一)无约束优化概述
机器学习笔记之优化算法——无约束优化概述
- 引言
-
- 回顾:关于支持向量机的凸二次优化问题
- 无约束优化问题概述
-
- 解析解与数值解
- 数值解的单调性
- 关于优化问题的策略
-
- 线搜索方法
- 信赖域方法
引言
从本节开始,将介绍优化算法 ( Optimization Algorithm ) (\text{Optimization Algorithm}) (Optimization Algorithm)。
回顾:关于支持向量机的凸二次优化问题
基于支持向量机 ( Support Vector Machine,SVM ) (\text{Support Vector Machine,SVM}) (Support Vector Machine,SVM)最大间隔分类器的朴素思想:从能够将所有样本点正确分类的直线中找到满足条件的一条直线:数据集 D \mathcal D D内的 N N N个样本点到直线对应的 N N N个距离中找出长度最小的距离,而从所有直线中找出最小距离长度最大的那条直线即为所求。
也就是说,在样本点分类正确的条件下,任意一条直线与 D \mathcal D D中的样本点之间均会存在一个最小距离,而‘最小距离’这个值最大意味着该直线是 D \mathcal D D划分正确的最优模型结果,无论是正类还是负类,该直线均与其保持一定距离。
- 关于数据集 D \mathcal D D的描述表示如下:
D = { ( x ( i ) , y ( i ) ) } i = 1 N x ( i ) ∈ R p ; y ( i ) ∈ { − 1 , + 1 } \mathcal D = \left\{(x^{(i)},y^{(i)})\right\}_{i=1}^N \quad x^{(i)} \in \mathbb R^{p};y^{(i)} \in \{-1,+1\} D={(x(i),y(i))}i=1Nx(i)∈Rp;y(i)∈{−1,+1} - 关于模型的描述表示如下:
y = W T x + b y = \mathcal W^T x + b y=WTx+b
这意味着:若将 D \mathcal D D中所有样本点均分类正确 ⇔ \Leftrightarrow ⇔ 每个样本的预测结果 W T x ( i ) + b \mathcal W^T x^{(i)} + b WTx(i)+b与对应标签同号。即:
y ( i ) ( W T x ( i ) + b ) > 0 ∀ ( x ( i ) , y ( i ) ) ∈ D y^{(i)} \left(\mathcal W^T x^{(i)} + b\right) > 0 \quad \forall (x^{(i)},y^{(i)}) \in \mathcal D y(i)(WTx(i)+b)>0∀(x(i),y(i))∈D
经过函数间隔 ( Functional Margin ) (\text{Functional Margin}) (Functional Margin)的约束,对应最大间隔分类器的化简结果表示如下:
{ max W , b 1 ∣ ∣ W ∣ ∣ min ( x ( i ) , y ( i ) ) ∈ D y ( i ) ( W T x ( i ) + b ) s . t . y ( i ) ( W T x ( i ) + b ) > 0 ⇒ { min W , b 1 2 W T W s . t . y ( i ) ( W T x ( i ) + b ) > 0 \begin{aligned} & \begin{cases} \begin{aligned} & \mathop{\max}\limits_{\mathcal W,b} \frac{1}{||\mathcal W||} \mathop{\min}\limits_{(x^{(i)},y^{(i)}) \in \mathcal D} y^{(i)} (\mathcal W^T x^{(i)} + b) \\ & s.t. y^{(i)} (\mathcal W^T x^{(i)} + b) > 0 \end{aligned} \end{cases} \\ \Rightarrow & \begin{cases} \begin{aligned} & \mathop{\min}\limits_{\mathcal W,b} \frac{1}{2} \mathcal W^T \mathcal W \\ & s.t. \quad y^{(i)} (\mathcal W^T x^{(i)} + b) > 0 \end{aligned} \end{cases} \end{aligned} ⇒⎩ ⎨ ⎧W,bmax∣∣W∣∣1(x(i),y(i))∈Dminy(i)(WTx(i)+b)s.t.y(i)(WTx(i)+b)>0⎩ ⎨ ⎧W,bmin21WTWs.t.y(i)(WTx(i)+b)>0
观察上式。很明显,它是一个包含 N N N个不等式约束的凸二次优化问题:
- 其中,目标函数 1 2 W T W \begin{aligned}\frac{1}{2} \mathcal W^T\mathcal W\end{aligned} 21WTW是一个二次型函数:
f ( W ) = 1 2 W T W = 1 2 ( w 1 2 + w 2 2 + ⋯ + w p 2 ) \begin{aligned} f(\mathcal W) & = \frac{1}{2} \mathcal W^T\mathcal W \\ & = \frac{1}{2} (w_1^2 + w_2^2 + \cdots + w_p^2) \end{aligned} f(W)=21WTW=21(w12+w22+⋯+wp2) - N N N个约束是由仿射函数 ( Affine Function ) (\text{Affine Function}) (Affine Function)构成的不等式约束:
g ( W , b ) = 1 − y ( i ) ( W T x ( i ) + b ) = 1 − y ( i ) ( w 1 ⋅ x 1 ( i ) + ⋯ + w p ⋯ x p ( i ) + b ) i ∈ { 1 , 2 , ⋯ , N } \begin{aligned} g(\mathcal W,b) & = 1 - y^{(i)}(\mathcal W^T x^{(i)} + b) \\ & = 1 - y^{(i)} \left(w_1 \cdot x_1^{(i)} + \cdots + w_p \cdots x_p^{(i)} + b\right) \quad i \in \{1,2,\cdots,N\} \end{aligned} g(W,b)=1−y(i)(WTx(i)+b)=1−y(i)(w1⋅x1(i)+⋯+wp⋯xp(i)+b)i∈{1,2,⋯,N}
凸二次优化问题必然有解,因而可以对最优参数 W ∗ , b ∗ \mathcal W^*,b^* W∗,b∗进行求解。首先,通过 KKT \text{KKT} KKT条件求解 W ∗ \mathcal W^* W∗的解析解,并找出支持向量;将支持向量带入,对 b ∗ b^* b∗进行求解。
求解思路见传送门
无约束优化问题概述
在工程设计中的优化问题,其一般提法是要选择一组参数(变量),在满足一系列的条件(约束)下,使设计指标(目标)达到最优值。
从是否存在约束条件的角度可将优化问题分为约束优化与无约束优化;从另一个角度也可以对优化问题进行划分:凸优化 ( Convex Optimization ) (\text{Convex Optimization}) (Convex Optimization)与非凸优化。
解析解与数值解
从无约束条件的凸优化开始,系统地介绍优化问题。
关于凸优化问题的目标函数 ( Objective Function ) (\text{Objective Function}) (Objective Function)表示如下:
这里对自变量 X \mathcal X X不进行过多约束,它仅是 n n n维实数空间中的点。
min X ∈ R n f ( X ) \mathop{\min}\limits_{\mathcal X \in \mathbb R^n} f(\mathcal X) X∈Rnminf(X)
-
如果函数 f ( X ) f(\mathcal X) f(X)是一个凸函数,并且它足够简单:例如 X \mathcal X X是一个一维随机变量;而 f ( X ) f(\mathcal X) f(X)是一个一元的、二次的凸函数,并且 X \mathcal X X定义域中连续、可微。这种情况下,我们完全不需要去求解数值解,直接通过求其解析解的方式来求得使 f ( X ) f(\mathcal X) f(X)取得最值的最优解。
-
但实际上,更多的优化问题我们没有办法通过求解解析解的方式获得。更多的,我们会使用数值解通过迭代的方式来逼近近似解。
数值解的基本思路:给定一个初始值 x 0 x_0 x0,通过某种具体策略对 x 0 x_0 x0进行迭代: x 1 , x 2 , x 3 , ⋯ x_1,x_2,x_3,\cdots x1,x2,x3,⋯。而数值解自身就是迭代过程中产生的数列结果:
这里的∞ \infty ∞仅仅是一种数学表达,从算法的角度,我们不可能让迭代无限地执行下去,在算法过程中,我们可能会设置一系列条件,当迭代结果x k x_k xk达到条件时,我们则认为近似解x k x_k xk已经足够精确,从而停止迭代过程。迭代停止后,这个近似解x k x_k xk有可能就是最优解x ∗ x^* x∗自身;也有可能是一个满足条件的一个效果不错的极小值。
{ x k } k = 1 ∞ \{x_k\}_{k=1}^{\infty} {xk}k=1∞
数值解的单调性
而单调性是指:随着迭代步骤的增加,数值解对应的函数结果尽量满足目标函数的优化方向。以上述目标函数 min X ∈ R n f ( X ) \begin{aligned}\mathop{\min}\limits_{\mathcal X \in \mathbb R^n} f(\mathcal X)\end{aligned} X∈Rnminf(X)为例,理想状态下的图像描述表示如下:
这仅仅是一个抽象的图像描述。

从上图可以明显观察到:随着数值解迭代次数的增加,对应函数结果向目标函数的优化方向(最小值)靠近,但不否认的是:靠近的幅度也在逐渐减小,说明迭代的数值解正在逐步逼近最优解 f ∗ f^* f∗。可以看出,该单调性是一个严格的单调性,即:
f ( x k + 1 ) < f ( x k ) f ( x k ) , f ( x k + 1 ) ∈ { f ( x k ) } k = 0 ∞ f(x_{k+1}) < f(x_k) \quad f(x_k),f(x_{k+1}) \in \{f(x_k)\}_{k=0}^{\infty} f(xk+1)<f(xk)f(xk),f(xk+1)∈{f(xk)}k=0∞
- 一些算法具备这种单调性的性质。如梯度下降法 ( Gradient Descent,GD ) (\text{Gradient Descent,GD}) (Gradient Descent,GD):
W ( t + 1 ) ⇐ W ( t ) − η ⋅ ∇ W J ( W ) \mathcal W^{(t+1)} \Leftarrow \mathcal W^{(t)} - \eta \cdot \nabla_{\mathcal W}\mathcal J(\mathcal W) W(t+1)⇐W(t)−η⋅∇WJ(W)
这种方法必然会使迭代产生的数值解 W ( 1 ) , W ( 2 ) , ⋯ , W ( k ) , W ( k + 1 ) , ⋯ \mathcal W^{(1)},\mathcal W^{(2)},\cdots,\mathcal W^{(k)},\mathcal W^{(k+1)},\cdots W(1),W(2),⋯,W(k),W(k+1),⋯满足:
J ( W ( k + 1 ) ) < J ( W ( k ) ) \mathcal J(\mathcal W^{(k+1)}) < \mathcal J(\mathcal W^{(k)}) J(W(k+1))<J(W(k))
但实际上,并不是所有算法都会严格按照上述单调性执行迭代。或者说,如果目标函数是复杂的(坑坑洼洼的,- -),如果使用梯度下降法,它可能更容易地陷入到局部极小值中,也就是说,在复杂的函数环境下,这种严格的单调性可能是不可取的。
如何降低单调性的严格程度 ? ? ?换句话说,我们是否可以增加一些关于单调性的容错率:从原始的严格单调性变为允许出现局部错误的单调性。也就是说:在迭代过程中,允许局部出现非单调性的情况,但整体趋势保持单调性。使用数学符号描述这一思想:依然以上述目标函数 min X ∈ R n f ( X ) \begin{aligned}\mathop{\min}\limits_{\mathcal X \in \mathbb R^n} f(\mathcal X)\end{aligned} X∈Rnminf(X)为例,在迭代过程产生的一系列数值解 x 1 , x 2 , ⋯ , x k , x k + 1 , ⋯ x_1,x_2,\cdots,x_{k},x_{k+1},\cdots x1,x2,⋯,xk,xk+1,⋯会满足:
f ( x k + 1 ) < f ( x k − m ) f ( x k + 1 ) , f ( x k − m ) ∈ { f ( x k ) } k = 0 ∞ ; m ∈ [ 0 , k ] f(x_{k+1}) < f(x_{k-m}) \quad f(x_{k+1}),f(x_{k-m}) \in \left\{f(x_k)\right\}_{k=0}^{\infty}; m \in [0,k] f(xk+1)<f(xk−m)f(xk+1),f(xk−m)∈{f(xk)}k=0∞;m∈[0,k]
上式中的 m m m可以看作是调节单调性严格程度的一个参数:
- 当 m = 0 m= 0 m=0时,迭代过程遵循严格的单调性;
- 随着 m m m的增加,从而削弱单调性的严格程度。例如: m = 3 m=3 m=3,仅需满足 f ( x k + 1 ) < f ( x k − 3 ) f(x_{k+1}) < f(x_{k-3}) f(xk+1)<f(xk−3)即可,而 f ( x k + 1 ) f(x_{k+1}) f(xk+1)与 f ( x k ) , f ( x k − 1 ) , f ( x k − 2 ) f(x_{k}),f(x_{k-1}),f(x_{k-2}) f(xk),f(xk−1),f(xk−2)之间的大小关系并不是关注的重点。
关于优化问题的策略
需要区分的是:这里提到的策略并不是损失函数,而是数值解的迭代方法。也就是说:如何在迭代过程中,通过已知数值解 x k x_k xk得到新的数值解 x k + 1 x_{k+1} xk+1。数学符号描述如下:
x k ⟹ ? x k + 1 \begin{aligned}x_{k} \overset{\text{?}}{\Longrightarrow} x_{k+1}\end{aligned} xk⟹?xk+1
这里介绍两种常见迭代策略:
线搜索方法
-
线搜索方法 ( Line Search Method ) (\text{Line Search Method}) (Line Search Method)。该方法的特点是:数值解的方向与步长分开执行:先定方向,再定步长。对应数学符号表达如下:
~~我并没有看到方向与步长的先后顺序,仅观察到了它们的分开执行。
x k + 1 = x k + α k ⋅ P k x_{k+1} = x_{k} + \alpha_k \cdot \mathcal P_k xk+1=xk+αk⋅Pk
其中 α k > 0 \alpha_k > 0 αk>0表示步长(机器学习中的学习率,实数); P k \mathcal P_k Pk表示方向。针对线搜索方法,步长的重要程度高于方向。也就是说,步长相较于方向对数值解结果的影响更大。原因在于:一旦策略被确定,方向的可操作空间是有限的。例如我们执行一个回归任务,我们使用的目标函数是均方误差 ( Mean Squared Error ) (\text{Mean Squared Error}) (Mean Squared Error),并使用梯度下降法作为优化策略。那么此时方向就是被约束的——目标函数最小值对应方向(负梯度方向)相关的方向。
相反,我们对于步长的要求更加严格。原因在于:
- 如果步长被设置的较大,可能会导致在数值解的迭代过程中错过最优值;甚至产生的新数值解不满足梯度下降法对应的严格的单调性;
这在实际过程中会表现出:损失函数结果反弹,或者是震荡现象。 - 如果步长被设置的较小,这会产生很高的时间代价。而这个代价在数值解的迭代过程中,可能是没有必要的。
- 如果步长被设置的较大,可能会导致在数值解的迭代过程中错过最优值;甚至产生的新数值解不满足梯度下降法对应的严格的单调性;
因而线搜索方法也被称作一维搜索方法。因为该搜索方法作用的对象并不是变量 X \mathcal X X自身,而是对应的步长 α \alpha α。由于 α \alpha α是人为设置的标量,是 1 1 1维特征,这也是一维搜索方法名称的由来。
信赖域方法
与线搜索方法中步长与方向分开执行不同的是,信赖域方法 ( Trust-Region Method ) (\text{Trust-Region Method}) (Trust-Region Method)对方向与步长进行综合考量。
假设在变量 X \mathcal X X的空间中,目标函数 f ( X ) f(\mathcal X) f(X)对应函数的等高线表示如下:
需要注意的点:这里的变量X \mathcal X X指的是模型的权重信息,而不是样本特征。因为样本是数据集给定的。因而这个二维空间指的是权重空间,对应登高线是损失函数在权重空间中的解区域;而红色部分是最优解区域,也就是说,位于红色区域的权重可以使f ( X ) f(\mathcal X) f(X)接近最优值,而红色区域的中心点对应的X ∗ \mathcal X^* X∗,有f ( X ∗ ) = min X ∈ R 2 f ( X ) \begin{aligned}f(\mathcal X^*) = \mathop{\min}\limits_{\mathcal X \in \mathbb R^2} f(\mathcal X)\end{aligned} f(X∗)=X∈R2minf(X)

以 x k x_k xk为圆心, Δ k \Delta_k Δk为半径做圆,圆内的所有描述权重的点可看做关于 x k x_k xk的邻域,而这个邻域也被称作信赖域;定义 n n n维向量 P \mathcal P P是以 x k x_k xk为起始点, x k x_k xk邻域内某一点为终止点的一个向量。那么该向量 P \mathcal P P自然存在约束。即:该向量的大小(二范式)不超过半径 Δ k \Delta_k Δk的大小。数学符号表达为:
∣ ∣ P ∣ ∣ ≤ Δ k ||\mathcal P|| \leq \Delta_k ∣∣P∣∣≤Δk
而我们要求解的目标是:在 x k x_k xk邻域中找到一个合适的点,该点与 x k x_k xk相连得到向量 P k \mathcal P_k Pk。而这个向量 P k \mathcal P_k Pk自身就是 x k x_k xk移动的方向与步长:
x k + 1 = x k + P k x_{k+1} = x_k+ \mathcal P_k xk+1=xk+Pk
对应图像描述表示如下:
其中长蓝色实线表示 x k x_k xk;短蓝色实线表示 P k \mathcal P_k Pk;长蓝色虚线表示 x k + P k x_k + \mathcal P_k xk+Pk.
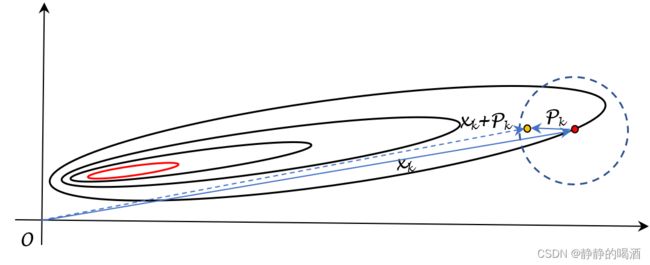
也就是说:这个 P k \mathcal P_k Pk必须满足:在半径 Δ k \Delta_k Δk邻域范围内, x k x_k xk和 P k \mathcal P_k Pk组成的新向量 x k + P k x_k + \mathcal P_k xk+Pk,与整个邻域内的所有变量的目标函数结果相比最小。数学符号表达如下:
首先,邻域内的任意一点,都可以表示为 x k + P x_k + \mathcal P xk+P的形式。
f ( x k + P k ) = min P ; Δ k f ( x k + P ) f(x_k + \mathcal P_k) = \mathop{\min}\limits_{\mathcal P;\Delta_k} f(x_k + \mathcal P) f(xk+Pk)=P;Δkminf(xk+P)
由于 x k x_k xk是上一时刻迭代产生的结果,是已知项,因此将上述表达转化为如下形式:
P k = arg min P ; Δ k f ( x k + P ) \mathcal P_k = \mathop{\arg\min}\limits_{\mathcal P;\Delta_k} f(x_k + \mathcal P) Pk=P;Δkargminf(xk+P)
而真实情况是:即便是仅在以 x k x_k xk为圆心, Δ k \Delta_k Δk为半径的邻域内,目标函数 f ( ⋅ ) f(\cdot) f(⋅)可能依然是复杂的(坑坑洼洼的~)。因此,我们使用泰勒展开式对 f ( x k + P ) f(x_k + \mathcal P) f(xk+P)进行化简:
由于泰勒展开式可以无限展开,这里仅展开到二次项,使用≈ \approx ≈表达。其中[ ∇ 2 f ( x k ) ] \left[\nabla^2 f(x_k)\right] [∇2f(xk)]在正则化——权重衰减角度中介绍过,被称作Hession Matrix \text{Hession Matrix} Hession Matrix,这里使用H k \mathcal H_k Hk对其进行表示。
f ( x k + P ) ≈ f ( x k ) + 1 1 ! [ ∇ f ( x k ) ] T P + 1 2 ! P T [ ∇ 2 f ( x k ) ] P ≈ f ( x k ) + [ ∇ f ( x k ) ] T P + 1 2 P T H k P \begin{aligned} f(x_k + \mathcal P) & \approx f(x_k) + \frac{1}{1!} \left[\nabla f(x_k)\right]^T \mathcal P + \frac{1}{2!} \mathcal P^T \left[\nabla^2 f(x_k)\right] \mathcal P \\ & \approx f(x_k) + \left[\nabla f(x_k)\right]^T \mathcal P + \frac{1}{2} \mathcal P^T \mathcal H_k \mathcal P \end{aligned} f(xk+P)≈f(xk)+1!1[∇f(xk)]TP+2!1PT[∇2f(xk)]P≈f(xk)+[∇f(xk)]TP+21PTHkP
观察上式,它是关于 P \mathcal P P的一个二次函数。至此,我们记 M k ( P ) \mathcal M_k(\mathcal P) Mk(P)是一个仅关于 P \mathcal P P的函数:
如果目标函数 f ( X ) f(\mathcal X) f(X)在 X \mathcal X X空间内连续可导,那么 H k \mathcal H_k Hk就是一个实对称矩阵。这也意味着:如果变量(权重)的维度 n n n如果过高,那么 H k \mathcal H_k Hk的计算代价也是极高的。
M k ( P ) = f ( x k ) + [ ∇ f ( x k ) ] T P + 1 2 P T H k P \mathcal M_k(\mathcal P) = f(x_k) + \left[\nabla f(x_k)\right]^T \mathcal P + \frac{1}{2} \mathcal P^T \mathcal H_k \mathcal P Mk(P)=f(xk)+[∇f(xk)]TP+21PTHkP
至此,将上述优化问题化简为如下形式:
不要忘记 P \mathcal P P自身的约束条件,将 arg min P ; Δ k f ( x k + P ) \mathop{\arg\min}\limits_{\mathcal P;\Delta_k} f(x_k + \mathcal P) P;Δkargminf(xk+P)中的 Δ k \Delta_k Δk转化为约束条件。
{ P k = arg min P M k ( P ) ∣ ∣ P ∣ ∣ ≤ Δ k \begin{cases} \mathcal P_k = \mathop{\arg\min}\limits_{\mathcal P} \mathcal M_k(\mathcal P) \\ ||\mathcal P|| \leq \Delta_k \end{cases} ⎩ ⎨ ⎧Pk=PargminMk(P)∣∣P∣∣≤Δk
很明显,这又是一个约束优化问题。我们假设这个 P k \mathcal P_k Pk是可求的,并且我们也求解出了 P k \mathcal P_k Pk。但回顾上述过程,由于我们仅将 f ( x k + P ) f(x_k + \mathcal P) f(xk+P)化简为二阶泰勒展开,因而我们不否认求解出的 P k \mathcal P_k Pk依然是一个近似值。因此,我们需要验证:这个近似求解出的 P k \mathcal P_k Pk是否有效。
如何判定 P k \mathcal P_k Pk是否有效 ? ? ?一个朴素的想法是:将求解出的 P k \mathcal P_k Pk代入到 x k + 1 = x k + P k x_{k+1} = x_k + \mathcal P_k xk+1=xk+Pk中,观察新数值解 x k + 1 x_{k+1} xk+1是否比 x k x_k xk更优秀即可。
我们构建这样一个评价函数 ρ k \rho_k ρk:
ρ k = f ( x k ) − f ( x k + P k ) M k ( 0 ) − M k ( P k ) \rho_k = \frac{f(x_k) - f(x_k + \mathcal P_k)}{\mathcal M_k(0) - \mathcal M_{k}(\mathcal P_k)} ρk=Mk(0)−Mk(Pk)f(xk)−f(xk+Pk)
观察:
-
其中分子均是目标函数 f ( ⋅ ) f(\cdot) f(⋅);分母是由 f ( x k + P ) f(x_k + \mathcal P) f(xk+P)转化得到的 M k ( ⋅ ) \mathcal M_k(\cdot) Mk(⋅)函数。
-
M k ( 0 ) \mathcal M_k(0) Mk(0)意味着 P = 0 \mathcal P=0 P=0时的 M k ( P ) \mathcal M_k(\mathcal P) Mk(P)结果,我们可以将 M k ( 0 ) \mathcal M_k(0) Mk(0)视作 f ( x k ) f(x_k) f(xk)的简化版——因为确实仅展开到二阶,高次项我们并没有展开。
-
关于分子: f ( x k ) − f ( x k + P k ) f(x_k) - f(x_k + \mathcal P_k) f(xk)−f(xk+Pk),它记录的是求解出的 P k \mathcal P_k Pk在真实目标函数 f ( ⋅ ) f(\cdot) f(⋅)中的差异性结果;
如果差值较大,意味着f ( x k + 1 ) f(x_{k+1}) f(xk+1)不仅小于f ( x k ) f(x_k) f(xk),并且还相差很多。着反而说明我们求解的P k \mathcal P_k Pk很优秀;相反,如果差值很小,反正验证了求解的P k \mathcal P_k Pk并没有有效地进行优化。 -
关于分母,它和分子的思想基本相同,只不过使用的并不是真正的目标函数,而是一个对目标函数简化后的函数信息。
由于 P k \mathcal P_k Pk是通过约束优化: { arg min P M k ( P ) s . t . ∣ ∣ P ∣ ∣ ≤ Δ k \begin{aligned} \begin{cases} \mathop{\arg\min}\limits_{\mathcal P} \mathcal M_k(\mathcal P) \\ s.t. \quad ||\mathcal P|| \leq \Delta_k \end{cases} \end{aligned} ⎩ ⎨ ⎧PargminMk(P)s.t.∣∣P∣∣≤Δk产生的结果,那么关于 M k ( 0 ) − M k ( P k ) > 0 \mathcal M_k(0) - \mathcal M_k(\mathcal P_k) > 0 Mk(0)−Mk(Pk)>0恒成立。继续观察两者的比值 ρ k \rho_k ρk,观察它具体意义:
-
如果 ρ k \rho_k ρk是一个负值,这意味着 f ( x k ) − f ( x k + P k ) f(x_k) - f(x_k + \mathcal P_k) f(xk)−f(xk+Pk)与 M k ( 0 ) − M k ( P k ) \mathcal M_k(0) - \mathcal M_k(\mathcal P_k) Mk(0)−Mk(Pk)之间异号。但 M k ( 0 ) − M k ( P k ) > 0 \mathcal M_k(0) - \mathcal M_k(\mathcal P_k) > 0 Mk(0)−Mk(Pk)>0恒成立,那么会出现如下逻辑:在简化版本函数 M k ( ⋅ ) \mathcal M_k(\cdot) Mk(⋅)中选择出的最优 P k \mathcal P_k Pk在真实目标函数中反而没有起到优化作用,这意味着其他的 P k \mathcal P_k Pk结果必然也不会起到优化作用。这意味着两个问题:
- P k \mathcal P_k Pk是无效结果,本次迭代不执行,即 x k + 1 = x k x_{k+1} = x_k xk+1=xk;
- 为什么会出现这种情况:这说明真实目标函数 f ( ⋅ ) f(\cdot) f(⋅)与简化后的函数 M k ( ⋅ ) \mathcal M_k(\cdot) Mk(⋅)之间差距极大。也就是说:简化函数 M k ( ⋅ ) \mathcal M_k(\cdot) Mk(⋅)无法有效地对 f ( ⋅ ) f(\cdot) f(⋅)进行近似。这说明:被 Δ k \Delta_k Δk所包含的邻域内,其真实目标函数 f ( ⋅ ) f(\cdot) f(⋅)在该邻域内依然是非常复杂的,复杂到其简化函数 M k ( ⋅ ) \mathcal M_k(\cdot) Mk(⋅)无法对其进行近似。具体做法是:缩小 Δ k \Delta_k Δk的数值,从而减小邻域范围,目的是使邻域内的真实目标函数 f ( ⋅ ) f(\cdot) f(⋅)的复杂度降低,从而更容易地被简化函数 M k ( ⋅ ) \mathcal M_k(\cdot) Mk(⋅)近似。
-
如果 ρ k \rho_k ρk是一个很小的正值,这意味着 f ( x k ) − f ( x k + P k ) f(x_k) - f(x_k + \mathcal P_k) f(xk)−f(xk+Pk)与 M k ( 0 ) − M k ( P k ) \mathcal M_k(0) - \mathcal M_k(\mathcal P_k) Mk(0)−Mk(Pk)之间虽然是同号,但 M k ( 0 ) − M k ( P k ) \mathcal M_k(0) - \mathcal M_k(\mathcal P_k) Mk(0)−Mk(Pk)远大于 f ( x k ) − f ( x k + P k ) f(x_k) - f(x_k + \mathcal P_k) f(xk)−f(xk+Pk)。
这种情况是第一种情况的缓和版。唯一的区别在于第一种情况是 P k \mathcal P_k Pk纯粹的无效;这种情况是 P k \mathcal P_k Pk起到的优化效果极小,几乎可以视作无效。处理方法与第一种情况相同;
-
ρ k \rho_k ρk是一个不小的正值,这说明从 M k ( ⋅ ) \mathcal M_k(\cdot) Mk(⋅)中选择的 P k \mathcal P_k Pk对真实目标函数 f ( ⋅ ) f(\cdot) f(⋅)的优化同样有效。此时直接执行下一次迭代即可;
-
ρ k \rho_k ρk是一个很大的正值,这正好和第一种情况相反: Δ k \Delta_k Δk邻域范围内 f ( ⋅ ) f(\cdot) f(⋅)反而小于简化版 M k ( ⋅ ) \mathcal M_k(\cdot) Mk(⋅)的复杂度,那么我们需要扩大邻域范围来增加 f ( ⋅ ) f(\cdot) f(⋅)的复杂度。具体做法是:执行下一次迭代,并且 Δ k + 1 > Δ k \Delta_{k+1} > \Delta_k Δk+1>Δk。
这种情况会使P k \mathcal P_k Pk点落在Δ k \Delta_k Δk邻域范围的边缘部分,实际上,它本可以落在更远的位置,只是Δ k \Delta_k Δk所在邻域限制住了它。
虽然看起来逻辑还是很明确的,但信赖域方法的难点在于如何证明上述流程是否能够收敛。
相关参考:
优化问题——百度百科
【优化算法】无约束优化-概述