图解LeetCode——698. 划分为k个相等的子集(难度:中等)
一、题目
给定一个整数数组 nums 和一个正整数 k,找出是否有可能把这个数组分成 k 个非空子集,其总和都相等。
二、示例
2.1> 示例 1:
【输入】 nums = [4, 3, 2, 3, 5, 2, 1], k = 4
【输出】 True
【说明】 有可能将其分成 4 个子集(5),(1,4),(2,3),(2,3)等于总和。
2.2> 示例 2:
【输入】 nums = [1,2,3,4], k = 3
【输出】 false
提示:
1<= k <= len(nums) <=160< nums[i] <10000- 每个元素的频率在
[1,4]范围内
三、解题思路
根据题目描述,我们需要将数组nums分成k组,且每组的总和相等。那么首先我们需要做的就是确定每组的总和是多少。即:sum(nums[]) / k。
为了便于匹配,我们将数组通过Arrays.sort进行排序,从而获得一个增序的有序数组。那么现在我们就可以进行一些初步判断,来确定是否满足题目约束,即:
条件一:
sum(nums[]) / k计算出来的平均每组总和是否为整数(用取余‘%’计算)。如果不是,则直接返回false。
条件二:针对排序后的数组中,最大的那个值是否 小于等于 每组总和。如果不是,则直接返回false。
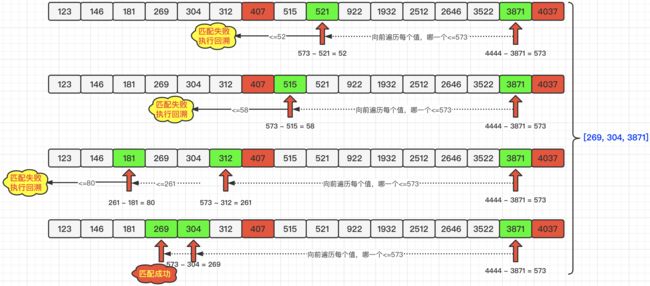
如果满足上面两个条件,我们就可以开始尝试进行分组匹配了。我们首先,从最大的元素开始遍历,再根据与每组平均总和的差值,再去继续寻找下面的元素,以下图为例,每组平均总和为:4444,最大元素为4037,差值为407;那么我们就需要再去寻找小于等于407的元素,发现在前面的元素中,存在407元素,那么匹配成功!为了防止被重复遍历,我们将4037和407都标记为已使用。如下图所示:
那么,寻找也并非一帆风顺的,比如:当我们继续遍历3871时,与4444的差值为573,我们向前寻找小于等于573的元素,找到512之后,计算差值为52,再向前寻找发现没有小于等于52的元素了,那就说明本次分组是失败了。我们就需要回溯操作了。什么是回溯呢?就是回到我们的上一步,继续匹配。具体流程如下图所示:
【注】在上图中,第三条寻找路径即:2871->312->181发现匹配失败后,其实是要试图匹配
2871->312->146和2871->312->123的,由于篇幅问题,就没有在图中展现出来。
剩下的遍历没有涉及回溯,与遍历第一次操作一样的,所以就不追溯了。详情请见下图:
四、代码实现
class Solution {
public static int[] numUsed;
public boolean canPartitionKSubsets(int[] nums, int k) {
numUsed = new int[nums.length];
Arrays.sort(nums);
int sum = Arrays.stream(nums).sum();
if (sum % k != 0 || nums[nums.length - 1] > sum / k) return false;
return divideGroups(nums, nums.length - 1, sum / k, 0, k);
}
public boolean divideGroups(int[] nums, int start, int target, int current, int k) {
if (k == 1) return true; // 分组操作执行k-1次之后,最后剩余的元素,就是最后一组了,不需要再匹配
if (current == target) return divideGroups(nums, nums.length - 1, target, 0, k - 1); // 分组操作执行k-1次后,最后剩余的元素,就是最后一组了,不需要再匹配
for (int i = start; i >= 0; i--) {
if (numUsed[i] == 1 || current + nums[i] > target) continue; // 被使用的元素,不能再次使用;总和大于目标值,也不能使用
numUsed[i] = 1; // 标记占用
if (divideGroups(nums, i - 1, target, current + nums[i], k)) return true;
numUsed[i] = 0; // 撤销标记
while (i > 0 && nums[i - 1] == nums[i]) i--; // 例如“12333333...”,假如最右侧的“3”这个值没有匹配上,那么它左侧的剩余五个“3”都不需要再匹配了。
}
return false;
}
}今天的文章内容就这些了:
写作不易,笔者几个小时甚至数天完成的一篇文章,只愿换来您几秒钟的 点赞 & 分享 。
更多技术干货,欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享,每天更新」