DFS学习总结

目录

1.介绍

2.快速理解​编辑

3.经典题目解析1

1.题目

2.解题思路

3.代码思路

4.代码实现

4.经典题目解析2

1.题目

2.解题思路

3.代码思路

4.代码实现

5.附录

---

1.介绍

概念：DFS(Depth FirstSearch),即深度优先搜索，顾名思义就是，按深度优先的顺序对 “问题状态空间”进行搜索的算法。

解读：问题状态空间，可以理解为一个问题每一步的所有可能的合状态，而对问题状态空间的搜索，相当于把问题的每一步都进行一个尝试，从而获得我们所需要的某种结果。按深度优先的顺序搜索的意思是，在每一种状态下任选一种状态延续下去一直持续到边界然后返回上一种状态，重复前面的过程的搜索方式。

2.快速理解

DFS搜索图示理解：DFS的表现形式，可用数据结构中的树的形式表现出，所以我们选择使用图1来简单演示DFS搜索形式。

若由状态1开始，从状态2、3、4里进行选择下一个状态，若先选择状态2，在选择状态2后，再从状态2后的两个状态5、6里选择下一个状态，若选择状态5，在选择状态5后，经判定发现到达了问题边界，则说明你已经通过DFS,搜索到了1种能到问题边界的状态序列了，然后可以进行某种你想要进行的操作。之后开始回溯，回溯至上一个状态，即状态2，由状态2再进行一次状态选择，因为状态5已经选择过了，那就没有必要再去选择了，因此选择状态6，在选择状态6后，经判断发现到达了问题边界，进行某种操作，然后回溯至上一个状态，即状态2，在状态2进行状态选择发现，可以选择的状态都已经选择过了，所以由状态2回溯至状态1。

由状态1选择状态2后所有可能的状态选择都搜索过了，得到的状态搜索序列为

1->2->5->2->6->2->1

同理，由状态1选择状态3，由状态1选择状态4所得到的搜索序列分别为

1->3->7->3->8->3->1

1->4->9->4->10->4->1

当由状态1选择状态2,3,4后进行一个搜索，三种状态搜索完毕，那么整个DFS就结束了。

3.经典题目解析1

1.题目

题目来源：AcWing

排列数字

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式

共一行，包含一个整数 n。

输出格式

按字典序输出所有排列方案，每个方案占一行。

数据范围

1≤n≤7

输入样例：

3

输出样例：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

2.解题思路

这是个很典型的DFS题目，n个数的排列方法，我们可以将每一个位数的排列可能当做一种状态，一位数确定了，就代表这一位的状态确定了，当每一位数都确定了，就代表到达问题边界了。

拿n==3时举例

 当什么都没有填时，为初始状态，那第一位填哪一个数字呢？根据题目要求，要按字典序来进行输出，那我们优先选择数字小的来填。那当第一位填1时，是一种状态，然后进行状态选择，因为题目要求的每一种排序是没有重复数字的，那么我们只能在2和3里面选，因字典序要求，我们第二位填2，那么第三位只能选择填剩下的3了，至此全部的数就填完了，也就是到达问题边界了，然后根据题目要求，输出这次的排序。

然后回溯，返回至填第二位的状态，因为第二位已经填过2了，所以选3，则第三位只能填2，三位数都填完了，到达了问题边界，因此输出这次的排序，重复这样的过程。

另外两种填第一位后状态的变化过程如下所示

_ _ _->2_ _->21_->213->21_->23_->231->23_->2_ _

_ _ _->3_ _->31_->312->31_->32_->321->32_->3_ _

所以要用DFS来解决这个问题，我们首先要确定状态已经进行了多少个，什么时候到达问题边界，回顾刚刚的过程，我们发现，我们是通过当前填的位数来确定状态进行了多少，到没到问题边界。由可以选择的状态里选择一种，填完了第一位，就表示状态进行了一个，填完了第二位，就代表状态进行了2个，填完了第三位，就代表状态进行了3个，数都填完了，到达了问题边界，然后就进行输出操作，然后回溯。确定了状态进行了多少个，那我们就可以由当前的状态，进入到下一步的状态，如填完1后接着填2等等。

当所有的状态都搜索完后，DFS就结束了。

3.代码思路

n:要排序的数字1~n

t:状态进行的个数

a[]:用于存储当前已经选择的数字

b[]:用于判断该数字是否可以选择

编写1个函数dfs,初始时每一位都没有填，说明状态进行了0个，所以刚开始调用dfs函数的t=0。

dfs函数的编写，首先要确定问题边界t==n时，即填完了n个位数后，此时进行输出操作。若没有到达问题边界，则根据题目要求的按字典序排列的要求，我们从数小的数字1开始枚举到n,若当前的数经判断满足(!b[i]),代表该数没有被选用，则此次可以选用，则将其填入当前位，即第t位a[t]上。同时，将b[i]由false，改为true，代表该数已被使用。然后dfs(t+1),意思是当前位已填完，所以t+1，然后调用dfs(),在当前选择的状态下进行下一个状态的选择，当函数dfs结束返回至调用处后，将b[i]由true，改为false,表示这一位填这个数字的状态已经选择过了，也意味着填这个数所能延续下去的状态都搜索完了，现在需要换别的数字填，就把这个数被使用的状态改回未使用。

4.代码实现

#include

using namespace std;

const int N=10;
int n;
int a[N];
bool b[N];

void dfs(int t)
{
    if(n==t)
    {
        for(int i=0;i>n;
    dfs(0);
    return 0;
}

4.经典题目解析2

1.题目

题目来源：AcWing

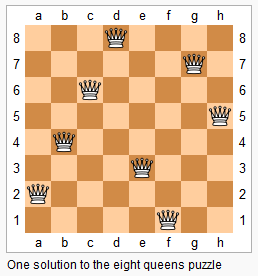
n-皇后问题

n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数 n。

输出格式

每个解决方案占 n 行，每行输出一个长度为 n 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

1≤n≤9

输入样例：

4

输出样例：

.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

2.解题思路

题意：题目要求在n*n的棋盘内，按要求放置n个皇后。

如果通过DFS来解决这个问题，那我们需要先找到解决问题的每一步时的状态，以及可选择延续下去的状态，以及问题边界。

根据题意可知，我们可以通过在每一个格子上进行放置皇后的尝试，从而找到将n个皇后都放置完的方法。那现在在哪一个格子上进行选择，已经放置了多少个皇后，就是解决问题时每一步的状态。在每一个格子上放皇后和不放皇后，就是我们要找的解决问题的每一步对应的可选择延续下去的状态。问题边界为在n*n的棋盘内，已放好的皇后数是否等于n。

所以，我们每一次的状态有，当前格子的行数和列数，以及已放置皇后数。问题边界就编写为，当现在的状态进行到了最后一个格子时，对皇后数进行判断，若皇后数等于n就输出该方案。若没有到达问题边界则对当前格子放不放皇后两种操作都进行选择。

3.代码思路

x:当前格子的行数

y:当前格子的列数

s:皇后放置个数

g[][]:用来存储输出满足条件的棋子的摆法。

row[]:判断该皇后放置的行，是否可行。

col[]:判断该皇后放置的列，是否可行。

dg[]:判断该皇后放置的斜线，是否可行。

udg[]:判断该皇后放置的对称斜线，是否可行。

在完成输入后，先对g[]进行预处理，让其全部存储“.”。然后调用dfs函数，其初始状态为（0,0,0）,代表刚开始在已放置了0个皇后，0行0列的格子上进行选择。

先确定问题边界，当x==n-1,y==n时，说明从0行0列枚举到n-1行n-1列已经完成了，而因为我们每次改变当前状态是通过dfs(x,y+1, )，即当前列数加1的方式,所以当完成所有格子的枚举后，y==n，若同时s==n,则代表n个皇后都已经放置完了，则输出棋子摆放的位置。

因为我们每次，通过y+1，来从上一个状态延续到下一个状态，所以我们加个判断当y==n时,让y=0,同时x++，达到从上一行的最后一列+1处，转为下一行的第一列，从而实现由0行0列枚举到n-1行n-1列。

在进行状态选择时，有两种选择，一是这个格子不放皇后，因此dfs(x,y+1,s）进入下一个状态。二是这个格子放皇后，如果这个格子要放皇后，则对这个格子的行列以及斜线进行判断，是否能放皇后（斜线判断方法请看附录），若是不能放则return。如果能放则让g[x][y]='Q'，说明该格子已经放了皇后，同时将皇后所在的行列以及斜线对应的数组元素改为true，代表已使用，然后dfs(x,y+1,s+1),s+1代表皇后放置了一个。 

当dfs返回后，再将标记的行列以及斜线对应的数组元素改为false,同时将该格子g[x][y]=‘.’代表该格子没有放皇后。

4.代码实现

#include

using namespace std;

const int N=20;
int n;
char g[N][N];
bool row[N],col[N],dg[N],udg[N];

void dfs(int x,int y,int s)
{

    if(x==n-1&&y==n)
    {
        if(s==n)
        {
            for(int i=0; i>n;
    for(int i=0; i

5.附录

斜线的一般方程为y=kx+b。而一个n*n的棋盘其k值很容易证明为1，所以该棋盘任意一条斜线的方程为y=x+b，等价于y-x=b（b为常数）。

所以每一个皇后对应的一条斜线为行减列,即x-y。因为行减列可能为负数，所以在方程左右同时加一个常数（n==20），来使得其对应的数为一个正数，这样对应到数组的下标就为正数了。

对称斜线同理，y=-x+b，y+x=b，即每一个皇后对应的对称斜线为x+y。