算法设计与分析——第五章回溯法 0-1背包问题+最优装载问题

参考文章1
参考文章2
参考视频

1、0-1背包问题

问题： 给定n种物品和一背包。物品i的重量是wi，其价值为pi，背包的容量为C。问应如何选择装入背包的物品，使得装入背包中物品的总价值最大?

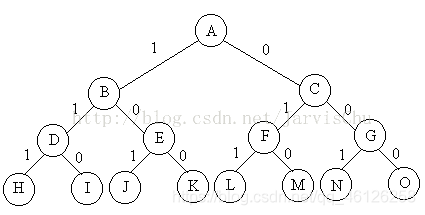
分析： 问题是n个物品中选择部分物品，可知，问题的解空间是子集树。比如物品数目n=3时，其解空间树如下图，边为1代表选择该物品，边为0代表不选择该物品。使用x[i]表示物品i是否放入背包，x[i]=0表示不放，x[i]=1表示放入。回溯搜索过程，如果来到了叶子节点，表示一条搜索路径结束，如果该路径上存在更优的解，则保存下来。如果不是叶子节点，是中点的节点（如B），就遍历其子节点（D和E），如果子节点满足剪枝条件，就继续回溯搜索子节点。

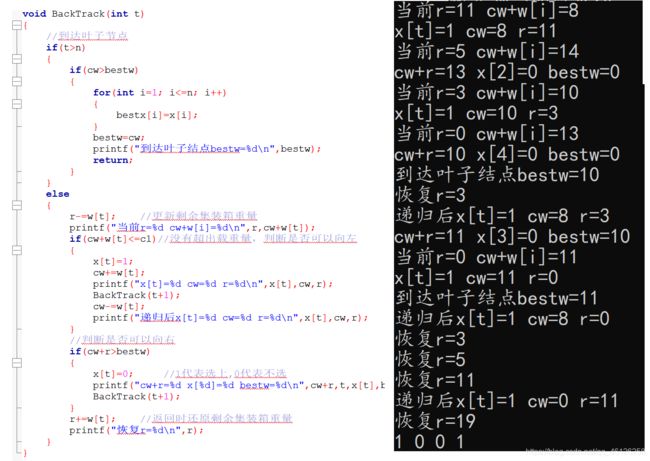
我觉得下面的代码更像是暴力，遍历所有的情况，然后更新最大价格以及最优解。

# include
#define NUM 100
using namespace std;
int n,c;  //物品数量 背包限制
int cw,cv,bestv; //当前重量 当前价值 最大价值
int w[100],v[100],x[100],bestx[100];  //最优载重,最优解

//t从1开始
void BackTrack(int t)
{
    if(t>n)
    {
        //更新bestv
        if(cv>bestv)
        {
            bestv=cv;
            for(int i=1; i<=n; i++)
                bestx[i]=x[i];
        }
    }
    else
    {
        for(int i=0; i<=1; ++i)
        {
            x[t]=i;
            if(i==0) //不放入背包
                BackTrack(t+1);
            else
            {
                if(cw+w[t]<=c)//放得下
                {
                    x[t]=1;
                    cw+=w[t];
                    cv+=v[t];
                    BackTrack(t+1);//进入下一结点
                    cw-=w[t];//从左子树回来要减掉左子树的w[t]
                    cv-=v[t];
                }
            }
        }

    }
}

int main()
{
    printf("请输入背包限制c：");
    cin>>c;
    printf("请输入物品数量n：");
    cin>>n;
    printf("依次输入物品的质量：");
    for(int i=1; i<=n; i++)
        cin>>w[i];
    printf("依次输入物品价值：");
    for(int i=1; i<=n; i++)
        cin>>v[i];
    BackTrack(1);
    printf("\n最优值：%d\n",bestv);
    printf("最优解：");
    for(int i=1; i<=n; i++)
        printf("%d ",bestx[i]);
    return 0;
}
/*
16
3
10 8 5
5 4 1
输出：
6
1 0 1
 
 
10
5
2 2 6 5 4
6 3 5 4 6
输出：
15
1 1 0 0 1

*/

2、装载问题

问题： 有一批共n个集装箱要装上2艘载重量分别为C1和C2的轮船，其中集装箱i的重量为wi，且∑wi≤C1+C2。要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。

例如，当n=3，c1=c2=50，且w=[10,40,40]时，可将集装箱1和2装上第一艘轮船，而将集装箱3装上第二艘轮船;如果w=[20,40,40]，则无法将这3个集装箱都装上轮船。

分析：
如果一个给定的装载问题有解，则我们采用的策略应该是：先将第一艘轮船尽可能装满，然后将剩余的集装箱上第二艘轮船（如果不能把所有物品装入第二艘船那么问题无解）。将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集，使该子集中集装箱重量之和最接近c1。由此可知，装载问题等价于特殊的0-1背包问题。

这个特殊的0-1背包问题可以这样理解：01背包是在物品总质量不超过c1时取出最大价值。而现在的背包重量为c1，我们一样要遍历所有的结点，要尽可能多地取出物品，使得最终的质量接近c1，在这里的最大价值就是背包的重量。

---

这样没有取出的物品就会被放到船2，再判断能不能把剩下的全部装入c2，不能则问题无解，能则得到了问题的解。

案例：
c1=c2=12 w=[8,6,2,3]
cw：当前的装载质量（从1到i累加）
r：当前剩余物品的累加质量（从i+1到n累加）
bestw：能放入船A的最大质量（最优值）

通过约束函数除去不可能的解，如果cw+w[i]<=c1，则可以将w[i]放入
通过上界函数除去不是最优的解，保证cw+r>bestw。
cw+r如果小于bestw则表示当前的cw把r中的剩余所有质量都加入，则不可能得到比bestw更大的质量了，那么就不需要继续对以此节点为根的树进行搜索计算了。所以要保证每个节点的cw+r>bestw，这表示继续对该节点进行搜索有可能得到更大的bestw。

参考文章
参考链接
（1）递归解决：
首先写递归出口，如果到达叶结点，若存在最优解就记录最优解，否则return;

没有到达叶结点，先考虑是否满足约束条件，若满足就加上该物品（进入左子树），将解加到解数组里面，更新cw即cw+=w[t]，再判断下一步(t+1)是否能左走，能则一直向左走，直到遇到叶结点或者cw+w[i]>c1则不能向左走。遇到叶子结点则更新bestw，bestx、不能向左走就只能判断能向右走。

然后就要考虑是否需要进入右子树，那就要判断当前的结点是否满足上界函数即cw+r>bestw：

• 满足则进入右子树，回溯到右子树必须得先回到父节点，那么之前在左边加上的质量就要减掉即cw-w[t]，然后才可以进入右子树即执行（t+1）步
• 不满足的话即便把所有的剩余质量都加到船上也不能达到更大的bestw，所以直接舍弃剩余右子树，不再进行搜索。

图解：（右子树同理）
和深度优先搜索一样的遍历顺序

代码：

# include
#define NUM 100
using namespace std;
int n;  //集装箱数量
int c1,c2;  //轮船载重量
int cw,r; //当前轮船载重量、剩余集装箱重量
int w[100],bestw,x[100],bestx[100];  //最优载重,最优解

//t从1开始
void BackTrack(int t)
{
    //到达叶子节点
    if(t>n)
    {
        if(cw>bestw)
        {
            for(int i=1; i<=n; i++)
            {
                bestx[i]=x[i];
            }
            bestw=cw;
            return;
        }
    }
    else
    {
        r-=w[t];    //更新剩余集装箱重量
        if(cw+w[t]<=c1)//没有超出载重量，判断是否可以向左
        {
            x[t]=1;
            cw+=w[t];
            BackTrack(t+1);
            cw-=w[t];
        }
        //判断是否可以向右
        if(cw+r>bestw)
        {
            x[t]=0;    
            BackTrack(t+1);
        }
        r+=w[t]; 
        //无论从左还是从右返回都还原剩余集装箱重量   
    }
}

int main()
{
    //读入数据；
    printf("请输入AB船的容量c1、c2:");
    cin>>c1>>c2;
    printf("输入物品的数量:");
    cin>>n;
    printf("依次输入物品的质量:");
    for(int i=1; i<=n; i++)//初始化，bestw=0
    {
        cin>>w[i];
        r+=w[i];
    }
    //递归回溯
    BackTrack(1);
    if(r-bestw>c2)//无解
        printf("没有装载方案\n");
    else//有解
        for(int i=1; i<=n; i++)
            printf("%d ",bestx[i]);
    return 0;
}
/*
12 12
4
8 6 2 3
*/