数据结构学习笔记(4)——数组、矩阵与广义表
数组
-
二维数组是元素为一元数组的一维数组。
-
数组一般采取顺序存储,最常见的两种操作是查找与修改。
-
二维数组元素的位置计算问题:假设有二维数组
a[m][n],数组从a[0][0]开始存储,问a[i][j]是数组中第几个元素?分析:m表示a的行数,n表示a的列数,且每行有n个元素,每列有m个元素。
a[i][j]表示的是数组a中第i+1行第j+1个元素,那么:- 行优先:
a[i][j]前面有i行,那么a[i][j]前面就有i*n+j个元素,则a[i][j]就是第i*n+j+1个元素 - 列优先:
a[i][j]前面有j列,那么a[i][j]前面就有j*m+i个元素,则a[i][j]就是第j*m+i+1个元素
- 行优先:
矩阵的压缩存储
矩阵
Amn即为一个矩阵的逻辑表示,在数据结构中,可以用一个二维数组来存储。
-
矩阵的转置
对于一个m×n的矩阵A[m][n],其转置矩阵是一个n×m的矩阵B[n][m],且有B[i][j]=A[j][i],0<=i
//矩阵转置 //二维数组统一设定成maxSize*maxSize的尺寸,maxSize是事先定义好的宏常量,表示可能出现的数组的尺寸最大值 void trsmat(int A[][maxSize], int B[][maxSize], int m, int n) { //遍历A,按照转置的定义挨个取值赋给B for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { B[j][i] = A[i][j]; } } } -
矩阵相加
矩阵相加按照Ci,j=Ai,j+Bi,j的规则,这说明m×n的两个矩阵相加后大小仍是m×n。
//矩阵相加 void addmat(int C[][maxSize], int A[][maxSize], int B[][maxSize], int m, int n) { for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { C[i][j] = A[i][j] + B[i][j]; } } } -
矩阵相乘
设A为m×n的矩阵,B为n×p的矩阵,那么称 的矩阵C为矩阵A与B的乘积,且只有在A矩阵的列数和B的行数相同时才有意义。矩阵C中的第i行第j列元素可以表示为:
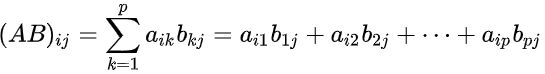
那么自然地,C的大小为m×p:
//矩阵相乘 void mutmat(int C[][maxSize], int A[][maxSize], int B[][maxSize], int m, int n,int p) { for (int i = 0; i < m; i++) { for (int j = 0; j < p; j++) { for (int k = 0; k < n; k++) { C[i][j] = A[i][k] * B[k][j]; } } } }
特殊矩阵与稀疏矩阵
特殊矩阵
-
对称矩阵
矩阵中的元素满足
a[i][j]=a[j][i]的矩阵称为对称矩阵。例:假设有一个n×n的对称矩阵,第一个元素为
a[0][0],请用一种存储效率较高的存储方式将其存在一个一维数组中。分析:对称矩阵满足主对角线上下方的元素对称相等,所以相同的元素只需要保存一份。那么所需要的一维数组的存储空间就是1+2+3+…+n个,即n(n+1)/2个元素。
按照行优先的顺序存储在一维数组中,矩阵元素与一元数组b中下标的对应关系为:
a元素 a[0][0] a[1][0] … a[n-1][0] … a[n-1][1] b下标 0 1 … (n-1)n/2 … n(n+1)/2-1 a 0 1 2 ... n //矩阵a的示意图,*表示元素 0 * 1 * * 2 * * * . . . n * * * ... * //取a的主对角线下半部分按照行优先的方式存储到一维数组b中b 0 1 2 3 4 5 n(n+1)/2-1 * |* *| * * *|...|****...*| -
三角矩阵
- 上三角阵:矩阵下三角部分(不包含对角线)的元素全为c(c可以是0)的矩阵
- 下三角阵:矩阵上三角部分(不包含对角线)的元素全为c(c可以是0)的矩阵
三角矩阵的存储方式与对称矩阵类似,但需要多存一个c元素,我们把它放在最后即可:
a元素 a[0][0] a[1][0] … a[n-1][0] … a[n-1][1] c b下标 0 1 … (n-1)n/2 … n(n+1)/2-1 n(n+1)/2 -
对角矩阵
如图是一个三对角矩阵,它的特点是除了主对角线以及其上下两条斜线上的元素外,其他元素均为c(c可以是0):

它的特点是除了首行和末行元素个数为2外,其余每行的元素个数都为3,据此来计算将其转化为一元数组后的下标问题。
稀疏矩阵
目前对于稀疏矩阵还没有一个明确统一的定义,在严版数据结构中的定义:
- 相同的元素或者零元素在矩阵中的分布存在一定规律的矩阵称为特殊矩阵,反之称为稀疏矩阵。
国外对于稀疏矩阵的普遍定义为:
- 矩阵中绝大多数元素都为0的矩阵称为稀疏矩阵。
稀疏矩阵的顺序存储
稀疏矩阵的绝大部分元素都没有必要存储,如何高效的存储剩余的元素就是稀疏矩阵压缩存储的关键。
常用的稀疏矩阵的顺序存储方法为:三元组表示法以及伪地址表示法。
-
三元组表示法
三元组数据结构的每个元素都含有三个变量:分别存储矩阵元素的值、行下标、列下标。
typedef struct{ int val; //值 int i; //行 int j; //列 }Trimat;假设有一个4阶的稀疏矩阵A如下图所示:
0 1 2 3 ——————————— 0| 0 0 0 1 1| 0 0 3 2 2| 1 0 0 0 3| 0 2 0 0里面含有5个非0元素,将其转换为三元组表示法即为:
val i j 5 4 4 1 0 3 3 1 2 2 1 3 1 2 0 2 3 1 可以看到,5个元素我们用了6个三元组结点,因为默认第1个结点的val存储非零元素的个数,i存储原矩阵的行数,j存储原矩阵的列数。以A[0][4]元素1为例,它的值为1,行坐标为0,列坐标为3,那么:
trimat[0].val=1; trimat[0].i=0; trimat[0].j=3;- 伪地址法
伪地址法即元素在矩阵中按照行优先或者列优先存储的相对位置。(第几个元素的意思)
伪地址法存储时每个元素只需要两个变量,即:值和伪地址。
比如上述矩阵A的最后一个非零元素2,按照行优先的规则它在矩阵中的位置就是i*4+j+1,即3*4+1+1=14。
对于一个m*n的稀疏矩阵a,a[i][j]的伪地址计算方法为(行优先):n*i+j+1。
稀疏矩阵的链式存储
最常见的稀疏矩阵的链式存储方法就是:邻接表法和十字链表法。
邻接表法就是将矩阵中的每一行的非零元素串成一个链表,每个链表结点中含有两个分量,一个是元素值,一个是列号。

在稀疏矩阵的十字链表存储结构中,矩阵的每一行用一个带头结点的链表表示, 每一列也用 一个带头结点的链表表示, 这种存储结构中的链表结点都有5个分量: 行分量、 列分量、数据域分量、指向下方结点的指针、指向右方结点的指针。
广义表
广义表: 表元素可以是原子或者广义表的一种线性表的扩展结构。
-
广义表的长度: 为表中最上层元素的个数
-
广义表的深度: 为表中括号的最大层数
-
表头 (Head) 和表尾 (Tail):当广义表非空时, 第 个元素为广义表的表头, 其余元素组成的表是 广义表的表尾。
举例说明:
-
A=( ), A 是个空表,长度为 0,深度为 1。 -
B=(d, e), B 的元素全是原子,即 d 和 e,长度为 2,深度为 1。 -
C=(b, (c, d)), C 有两个元素,分别是原子 b 和另一个广义表(c, d),长度为 2,深度为 2。
4)D=(B, C), D 的元素全是广义表,即 B 和 C, 长度为 2, 深度为 3。
由此可见,一个广义表的子表可以是其他已经定义的广义表的引用。
5)E=(a, E), E 有两个元素,分别是原子 a 和它本身,长度为 2。
由此可见,广义表可以是递归定义的,展开E可以得到(a,(a, (a, (a, · · ·)))) ,是无限深的广义表。
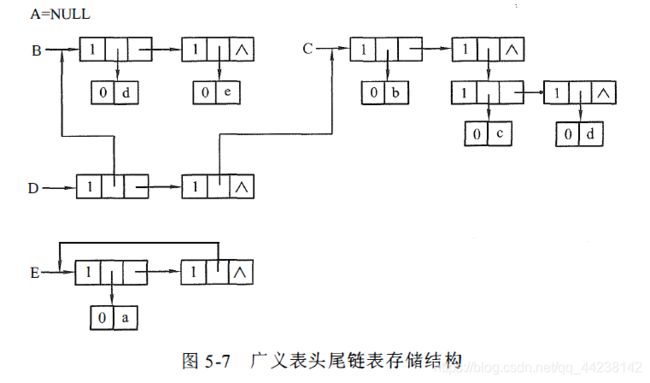
广义表的头尾链表存储结构
- 原子结点(2个域):标记域、数据域
- 广义表结点(3个域):标记域、头指针域、尾指针域
其中,对于广义表结点来说,
- 标记域用于区分当前结点是原子(用0来表示)还是广义表(用1来表示);
- 头指针域指向原子结点或者广义表结点;
- 尾指针域为空或者指向本层中的下一个广义表结点。
图5-7展示了1)到5)中广义表的头尾链表存储结构的存储情况:
A=()
B=(d,e)
C=(b,(c,d))
D=(B,C)
E=(a,E)
广义表的扩展线性表存储结构
,其中也有两种结点,即原子结点和广义表结点。
-
原子结点有3个域:标记域、数据域和尾指针域;
-
广义表结点也有3个域:标记域、头指针域与尾指针域。
其中,标记域区分当前结点是原子(用0来表示),还是广义表(用1来表示)。
扩展线性表存储结构类似带头结点的单链表存储结构,每一个子表都有一个不存储信息的头结点来标记其存在。
头尾链表存储结构类似于不带头结点的单链表存储结构。
图5-8展示了1)到5)中广义表的扩展线性表存储结构的存储情况:
A=()
B=(d,e)
C=(b,(c,d))
D=(B,C)
E=(a,E)
练习题
-
设数组A[0, ···, n-1]的n个元素中有多个零元素,设计一 个算法,将 A 中所有的非零元素依次移动到A数组的前端。
//将数组A中的非0字符移动到数组靠前的位置 int moveElem(int A[], int n) { int temp; for (int i = 0,j=0; i < n; i++) { if (A[i] != 0) { if (i != j) { temp = A[j]; A[j] = A[i]; A[i] = temp; } j++; } } } -
关于浮点型数组A[0, ···, n-1], 试设计实现下列运算的递归算法。
(1) 求数组A中的最大值。
(2) 求数组中n个数之和。
(3) 求数组中n个数的平均值。/*(1)分析:如果数组长度为1, 则可以直接返回最大值;否则将数组A视为两部分,即A[O]和A[l...,n-1]。如果A[0]大于A[1,...,n-1]中的最大值,则返回A[0], 反之按照上一步的方法递归地处理A[1]和A[2,...,n-1]。*/ float getMax(float A[], int i, int j) { float max; if (i == j) { return A[i]; } else { max = getMax(A, i + 1, j); if (A[i] > max) return A[i]; else return max; } } int main(){ ... getMax(A,0,n-1); }//递归求和,思路与上面类似 float getSum(float A[], int i, int j) { float sum; if (i == j) { return A[i]; } else { sum = getSum(A, i + 1, j); return A[i] + sum; } } int main(){ ... getSum(A,0,n-1); }//递归求平均值 float getAverage(float A[], int i, int j) { float ave; if (i == j) { return A[i]; } else{ ave = getAverage(A, i + 1, j); return (A[i] + (j - i) * ave) / (j - i + 1); } } int main(){ ... getAverage(A,0,n-1); } -
试设计一 个算法,将数组 A [0, · · ·, n-1]中所有奇数移到偶数之前。要求不另增加存储空间,且时间复杂度为O(n)。
//将数组 A [0, · · ·, n-1]中所有奇数移到偶数之前 void divide(int a[], int n) { int i = 0; int j = n - 1; int temp; while (i < j) { while (a[i] % 2 == 1 && i < j) //a从左往右遇到的第一个奇数 i++; while (a[j] % 2 == 0 && i < j) //a从右往左遇到的第一个偶数 j--; //交换后挪动i和j,向数组中间靠拢,当i==j时跳出循环 if (i < j) { temp = a[i]; a[i] = a[j]; a[j] = temp; i++; j--; } } }