数据结构——栈和队列
目录
1.栈
1.1栈的基本概念
1.2栈的顺序存储实现
1.3共享栈
1.4栈的链式存储实现
1.5栈在括号匹配中的应用
1.6栈在表达式求值中的应用
1.6.1中、前、后缀表达式
1.6.2后缀表达式⭐（中转后：手算+机算；后缀求值：手算+机算）
1.6.3前缀表达式（中转前：手算；前缀求值：机算⭐）
1.6.4中缀表达式（中缀求值：机算）
1.7栈在递归中的应用
2.队列
2.1队列的基本概念
2.2队列的顺序存储实现
2.3小结
2.3队列的链式存储实现
2.4双端队列
2.5队列的应用
3.特殊矩阵的压缩存储
3.1数组的存储结构
3.2特殊矩阵
栈和队列都是操作受限制的线性表。
1.栈
1.1栈的基本概念
栈（stack）：只能在一端进行（栈顶）插入/删除的线性表。故其逻辑结构为线性结构（一对一）。
线性表：具有相同数据类型的n个数据元素的有限序列。
栈的特点：后进先出（LIFO）
基本操作：
InitStack(&S) //初始化栈。构造一个空栈S，分配内存空间。
DestroyStack(&S) //销毁栈。销毁并释放栈S所占用的内存空间。
Push(&S,x) //进栈，若栈S未满，则将x加入使之成为新栈顶。
Pop(&S,&x) //出栈，若栈S非空，则弹出栈顶元素，并用x返回。
GetTop(S,&x) //读栈顶元素。若栈S非空，则用x返回栈顶元素
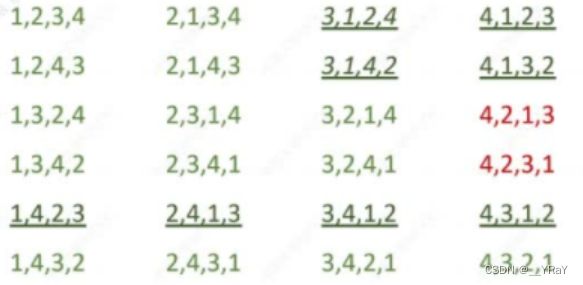
StackEmpty(S) //判断一个栈S是否为空。若S为空，则返回true,否则返回false 常考题型：已知进栈顺序，有哪些合法的出栈顺序？
n个不同元素进栈，出栈元素不同排列顺序个数为：
（卡特兰数Catalan），可用数学归纳法证明（不要求掌握）
1.2栈的顺序存储实现
顺序栈：逻辑结构——线性结构；存储结构（物理结构）——顺序存储
顺序栈的定义：
//顺序栈的定义：
#define maxsize 10
typedef struct {
ElemType data[maxsize]; //数据域（静态分配：静态数组）
int top; //栈顶指针（ 实际指的是该静态数组的数组下标，起到指针的作用）
}SqStack; //sequence stack基本操作1（top== -1时，即栈顶指针始终指向非空区域）
顺序栈的初始化：
void InitStack(SqStack &S){
S.top = -1; //设定-1代表空栈
} SqStack S; 声明一个顺序栈后，分配了连续的存储空间，大小为maxsize×sizeof（ElemType）
//栈空判断
bool StackEmpty(SqStack S){
if(S.top == -1) return true;
else return false;
} 顺序栈的进栈操作（增）：
bool Push(SqStack &S,ElemType x){
if(S.top == maxsize-1) return false; //栈满，无法再入栈，报错
// S.top = S.top + 1; //先移动栈顶指针
// S.data[S.top] = x; //新元素再入栈
S.data[++S.top] = x; //等价为一句 (top先加再用）
return true;
}顺序栈的出栈操作（删）：
bool Pop(SqStack &S,ElemType &x){
if(S.top == -1) return false;
// x = S.data[S.top]; //先删除元素，并由x代回
// S.top = S.top - 1; //再移动栈顶指针
x = S.data[S.top--]; //等价为一句 (top先用再减）
return true;
} 读栈顶元素操作（查）：
ElemType GetTop(SqStack S){
if(S.top == -1) return false; //栈空，报错
return S.data[S.top];
}
bool GetTop(SqStack S,ElemType &x){
if(S.top == -1) return false; //栈空，报错
x = S.data[S.top];
return true;
} 基本操作2（top== 0时，即栈顶指针始终指向下一个可插入的空区域）
顺序栈的初始化：
void InitStack(SqStack &S){
S.top = 0; //设定0代表空栈
}
//判空
bool StackEmpty(SqStack S){
if(S.top == 0) return true;
else return false;
}顺序栈的进栈操作（增）：
bool Push(SqStack &S,ElemType x){
if(S.top == maxsize) return false;
S.data[S.top++] = x; //top先用再加
return true;
}顺序栈的出栈操作（删）：
bool Pop(SqStack &S,ElemType &x){
if(S.top == 0) return false;
x = S.data[--S.top];//top先减再用
return true;
}读顺序栈的栈顶元素的操作（查）：
bool GetTop(SqStack S,ElemType &x){
if(S.top == 0) return false;
x = S.data[--S.top];
return true;
}top == -1 和 top == 0 的区别：（注意审题）
| 比较项 | top == -1 栈顶指针始终指向非空区域 |
top == 0 栈顶指针始终指向下一个可插入的空区域 |
| 栈空 | top == -1 | top == 0 |
| 栈满 | top == maxsize -1 | top == maxsize |
| push | S.top先加再用 | S.top先用再加 |
| pop | S.top先用再减 | S.top先减再用 |
1.3共享栈
共享栈：两个栈共享同一片存储空间。
定义与初始化：
//定义
#define maxsize 10
typedef struct{
ElemType data[maxsize];
int top0; //0号栈栈顶指针
int top1; //1号栈栈顶指针
}ShStack; //shared stack
//初始化
void InitShStack(ShStack &S){
//共享栈所占空间的头尾分别作为栈顶指针
S.top0 = -1;
S.top1 = maxsize;
} 栈满条件：top0+1 == top1
栈的销毁？——系统包分配包回收
在声明栈（Stack S）时，系统自动给栈分配空间；在所在生命域的生命周期结束后（如所在函数运行结束后），系统自动回收内存。
而上述中 top == -1 或 top == 0；都是在逻辑上的销毁。
1.4栈的链式存储实现
链栈：逻辑结构——线性结构；存储结构（物理结构）——链式存储
进栈/出栈只能在链栈的一端（栈顶）进行的单链表
链栈的定义：
//定义
typedef struct Linknode{
ElemType data;
struct Linknode *next;
}Linknode, *LiStack;
//等价于以下三句代码
struct Linknode{ //定义单链表的结点类型
ElemType data;//数据域 每个结点存放一个数据元素
struct Linknode *next;//指针域 指向单链表中下一个结点
};
typedef struct Linknode Linknode;
typedef struct Linknode* LiStack; 两种重命名后，声明时的区别：
Linknode * //强调这是一个结点
LiStack //强调这是一个单链表
//Linknode是个结构体，LiStack是（结构体）指针。两种重命名的灵活选择，可以提升代码可读性。
基本操作：
链栈的初始化（创）：
不带头结点
//初始化（创）
//不带头节点
bool InitLiStack(LiStack &S){
if(S == NULL) return false;//非法参数
S = NULL;
return true;
}带头结点
//初始化（创）
//带头节点
bool InitLiStack(LiStack &S){
S = (Linknode *)malloc(sizeof(Linknode));
if(S == NULL) return false;//内存不足，分配失败
S.next = NULL;
return true;
}链栈的判空：
//链栈的判空（带头结点）
bool LiStackEmpty(LiStack S){
if(S.next == NULL) return true;
else return false;
}链栈的进栈操作（增）：
//对应单链表对头结点的后插操作（头插法建立单链表）
bool Push(LiStack &S,ElemType x) {
//判满 ？
Linknode *p = (Linknode *)malloc(sizeof(Linknode));//新元素
if(p == NULL) return false; //内存不足，分配失败
p.data = x;
p->next = S.next;
S.next = p;//修改栈顶
return true;
}链栈的出栈操作（删）：
//对应单链表对头结点的后删操作
bool Pop(LiStack &S,ElemType &x) {
if(S.next == NULL) return false;//栈空 无法出栈 报错
x = S.next.data;
S.next == S.next.next; //修改栈顶
return true;
}读链栈的栈顶元素的操作（查）：
bool GetTop(LiStack S,ElemType &x){
if(S->next == NULL) return false;//栈空
x = S->next->data; //头节点后的的第一个元素
return true;
}1.5栈在括号匹配中的应用
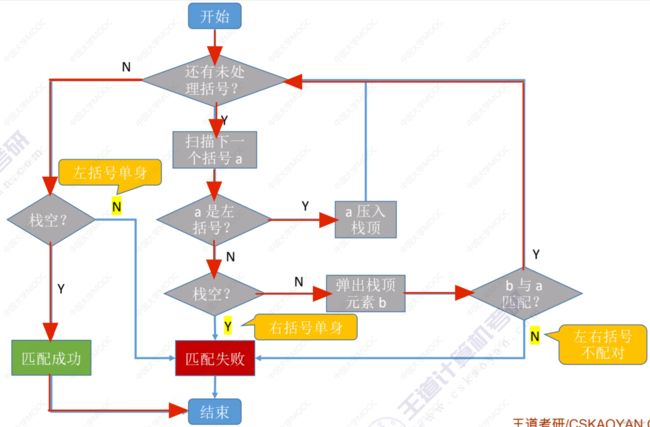
算法思路：遇到左括号 ( [ { 就入栈，遇到右括号 ) ] } 就“消耗”一个左括号（左括号出栈）。具体情形和算法流程图如下：
情形一（ok）：所有括号都能两两配对；
情形二（non-ok）：当前扫描到的右括号与栈顶的左括号不匹配，则该右括号及其之后的括号被视为非法括号，不再被扫描；
情形三（non-ok）：扫描到右括号，但栈空——右括号单身，则该右括号及其之后的括号被视为非法括号，不再被扫描；
情形四（non-ok）：处理完所有括号后，栈非空——左括号单身。
算法实现（顺序栈）：
（考试中 InitStack；StackEmpty；Push；Pop 均可直接使用 ，建议简要说明各接口）
//括号匹配(顺序栈实现）
bool bracketMatch(char[] str,int length){//已知括号数组和该数组长度
SqStack S;
InitStack(S);
for(int i=0 ; i1.6栈在表达式求值中的应用
1.6.1中、前、后缀表达式
表达式由操作数、运算符、界限符（括号）组成。（DIY概念：左操作数、右操作数）
一个灵感：可以不用界限符也能无歧义地表达运算顺序——前、后缀表达式
后缀表达式 = 逆波兰表达式（Reverse Polish notation）
前缀表达式 = 波兰表达式（Polish notation）
中、前、后代表运算符相对于本次运算操作数的位置（注意整体思想的运用）
一个中缀表达式可以对应多个前、后缀表达式。（”左优先“和”右优先“原则保证了顺序的唯一性，从而保证了算法的确定性）
1.6.2后缀表达式⭐（中转后：手算+机算；后缀求值：手算+机算）
1.中缀表达式转后缀表达式（手算）
中缀转后缀的手算方法：
①确定中缀表达式中各个运算符的运算顺序；
②选择下一个运算符，按照「左操作数 右操作数 运算符」的方式组合成一个新的操作数；
③如果还有运算符没被处理，就继续②。
“左优先”原则：只要左边的运算符能先计算，就优先算左边的（可保证算法的确定性，手算和机算结果相等）。
2.中缀表达式转后缀表达式（机算）
初始化一个栈，用于保存暂时还不能确定运算顺序的运算符。从左到右处理各个元素,直到末尾。可能遇到三种情况:
①遇到操作数。直接加入后缀表达式。
②遇到界限符。遇到 “(” 直接入栈；遇到 “)” 则依次弹出栈内运算符并加入后缀表达式，直到弹出 “(” 为止。注意："("、")"不加入后缀表达式。
③遇到运算符。依次弹出栈中优先级高于或等于（对比左优先原则）当前运算符的所有运算符（如 */优先级高于+-），并加入后缀表达式，若碰到 “(” 或栈空则停止弹出。然后再把当前运算符入栈。
按上述方法处理完所有字符后，将栈中剩余运算符依次弹出，并加入后缀表达式。
下面给出两个例子：
例1：
例2：
考察：（选择题）问到具体某一步遇到某种字符，如何处理
可以先用伪代码实现一下中缀表达式转后缀表达式（机算），模拟栈的变化过程
下面有一个练习：
注意：这个练习会出现栈溢出的问题。
综上，中转后 + 后缀求值 = 中缀求值。
3.后缀表达式求值（手算）
后缀表达式的手算方法（选择题）：
从左往右扫描，每遇到一个运算符，就让运算符前面最近的两个操作数执行对应运算，合体为一个操作数。（注意:两个操作数的左右顺序）
特点：最后出现的操作数先被运算——LIFO（栈的特点）
4.后缀表达式求值（机算）——用栈实现后缀表达式的计算⭐
①从左往右扫描下一个元素，直到处理完所有元素；
②若扫描到操作数则压入栈，并回到①；否则执行③；
③若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，回到①。（注意：先出栈的是”右操作数“）
最后栈中只会留下一个元素，就是最终结果。
后缀表达式适用于基于栈的编程语言（stack-oriented programming language），如：Forth、PostScript
1.6.3前缀表达式（中转前：手算；前缀求值：机算⭐）
1.中缀表达式转前缀表达式（手算）
中缀转前缀的手算方法:
①确定中缀表达式中各个运算符的运算顺序；
②选择下一个运算符，按照「运算符 左操作数 右操作数」的方式组合成一个新的操作数；
③如果还有运算符没被处理，就继续②。
“右优先”原则:只要右边的运算符能先计算，就优先算右边的。
2.前缀表达式求值（机算）——用栈实现前缀表达式的计算⭐
①从右往左扫描下一个元素，直到处理完所有元素；
②若扫描到操作数则压入栈，并回到①;否则执行③；
③若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，回到①；（注意：先出栈的是“左操作数”）。
综上，中转前 + 前缀求值 = 中缀求值。
1.6.4中缀表达式（中缀求值：机算）
根据上述，理论上有两种中缀表达式的计算，即中转后算法 + 后缀求值算法 = 中缀求值算法；中转前算法 + 前缀求值算法 = 中缀求值算法。
中缀表达式求值（机算）——用栈实现中缀表达式的计算（中转后算法+后缀求值算法）
中转后算法中，栈是用来存放暂时还不能确定生效次序的运算符——运算符栈；
后缀求值算法中，栈是用来存放暂时还不能确定运算次序的操作数——操作数栈。
故，初始化两个栈，操作数栈 和 运算符栈。
若扫描到操作数，压入操作数栈。
若扫描到运算符或界限符，则按照“中缀转后缀”相同的逻辑压入运算符栈（期间也会弹出运算符，每当弹出一个运算符时，就需要再弹出两个操作数栈的栈顶元素并执行相应运算，运算结果再压回操作数栈)
先回顾一下中转后算法、后缀求值算法的算法思路：
下面给出一个例子：
1.7栈在递归中的应用
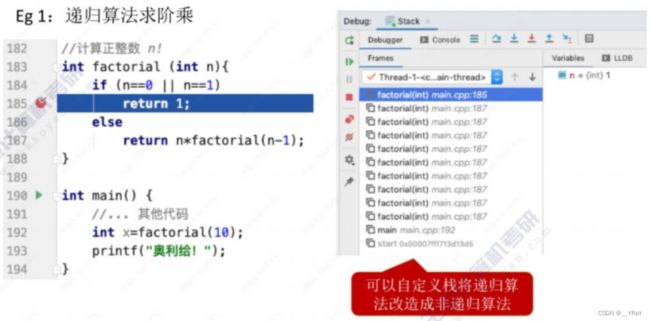
函数调用的特点：最后被调用的函数最先执行结束（LIFO)
函数调用时，需要用一个栈存储：调用返回地址；实参；局部变量
适合用“递归”算法解决——可以把原始问题转换为属性相同，但规模较小的问题。
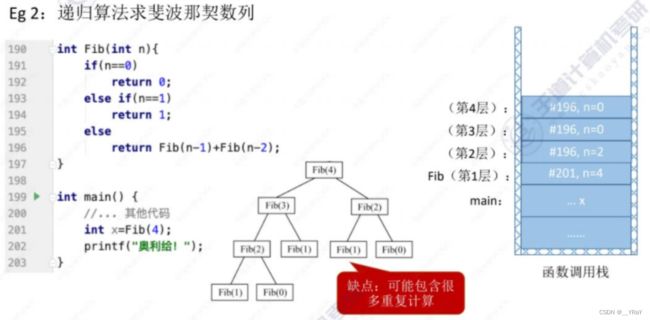
圈中的都需要重复计算！
递归调用时，函数调用栈可称为“递归工作栈”
每进入一层递归，就将递归调用所需信息压入栈顶；每退出一层递归，就从栈顶弹出相应信息。
缺点:太多层递归可能会导致栈溢出；可能会包含很多重复计算。
2.队列
2.1队列的基本概念
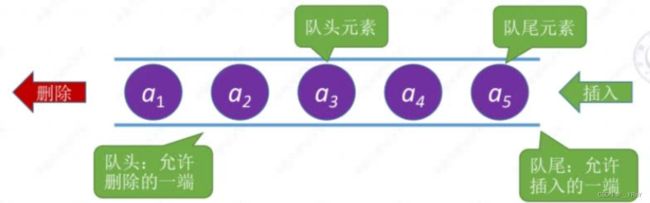
队列（Queue）：只能在一端（队尾）进行插入（入队），在另一端（队头）进行删除（出队）的线性表。故其逻辑结构为线性结构（一对一）。
线性表：具有相同数据类型的n个数据元素的有限序列。
队列的特点：先进先出（FIFO）
基本操作：
InitQueue(&Q) //初始化队列。构造一个空队列Q。（创）
DestroyQueue(&Q) //销毁队列。销毁并释放队列Q所占用的内存空间。（销）
EnQueue(&Q,x) //入队，若队列Q未满，则将x加入使之成为新队尾。（增）
DeQueue(&Q,&x) //出队，若队列Q非空，则删除队头元素，并用x返回。（删）
GetHead(Q,&x) //读队头元素。若队列Q非空，则用x返回队头元素（查：队列的使用场景中大多只访问队头元素）
QueueEmpty(Q) //判断一个队列Q是否为空。若Q为空，则返回true,否则返回false 2.2队列的顺序存储实现
顺序队列：逻辑结构——线性结构；存储结构（物理结构）——顺序存储
顺序队列的定义：
#define maxsize 10 //定义队列中元素的最大个数
typedef struct{
ElemType data[maxsize]; //用静态数组存放队列
int front,rear; //队头、队尾指针（实际是静态数组的下标，起到指针作用）
}SqQueue; //sequence queue
SqQueue Q; //声明一个队列（顺序存储），分配大小为maxsize×sizeof（ElemType）的连续存储空间基本操作：
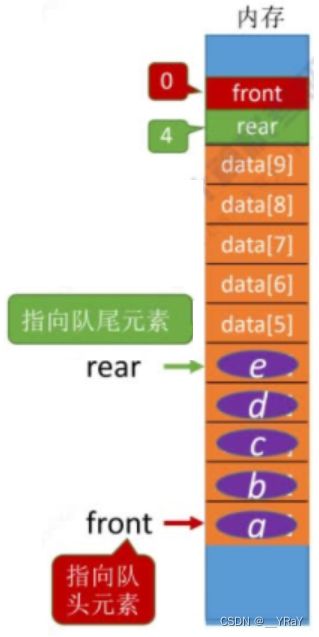
顺序队列的初始化（创）：
规定队头指向数组第一个元素，队尾指向下一个可插入的空区域（队尾的后一个位置）
//顺序队列的初始化（创）：
void InitQueue(SqQueue &Q){
Q.front = Q.rear = 0; //初始状态，队头队尾都指向数组第一个位置
} 顺序队列的判空操作：
队头队尾都指向数组第一个位置
//顺序队列的判空操作：
bool QueueEmpty(SqQueue Q){
if(Q.front == Q.rear) return true;
else returen false;
} 顺序队列的入队操作（增）：
//顺序队列的入队操作（增）：
bool EnQueue(SqQueue &Q,ElemType x){
if((Q.rear+1)%maxsize == Q.front) return false; //队满 报错
Q.data[Q.rear] == x; //新元素入队
Q.rear == (Q.rear+1)%maxsize; //队尾指针后移取模
return true;
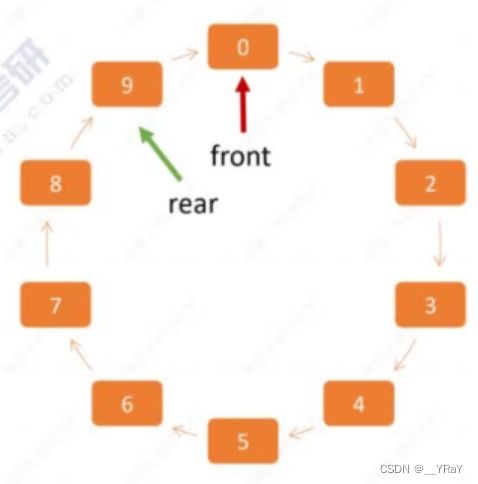
}取模（取余）：a%b——求a除以b的余数（a mod b）；
把无限的整数域映射到有限的整数集合 {0，1，2……}上 ；
%maxsize {0,1,2……maxsize-1} 将线状的存储空间在逻辑上变成了“环状”，可以重复利用静态数组所在的存储空间。——循环队列
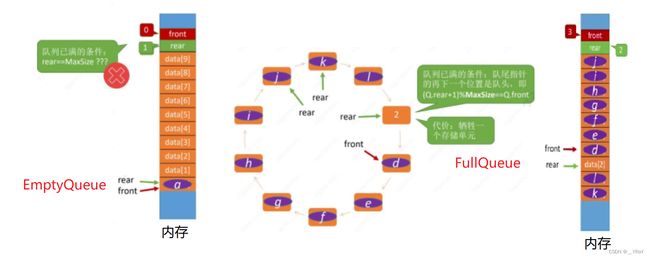
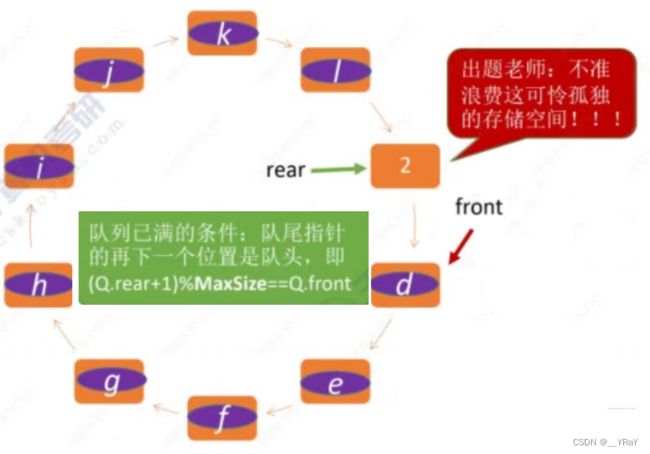
顺序队列的判满操作：
队满条件：队尾指针的下一个位置是对头（实际队列中有一个空位置）
//顺序队列的判满操作：
bool QueueFull(SqQueue Q){
if((Q.rear+1)%maxsize == Q.front) return true; //队尾指针的下一个位置是对头（实际队列中有一个空位置）
else return false;
}
顺序队列的出队操作（删）：
//顺序队列的出队操作（删）：
bool DeQueue(SqQueue &Q，ElemType &x){
if(Q.rear == Q.front) return false; //队空报错
x = Q.data[Q.front];
Q.front = (Q.front+1)%maxsize;
return true;
}获取顺序队列对头操作（查）：
//获取顺序队列对头操作（查）：
bool GetHead(SqQueue Q，ElemType &x){
if(Q.rear == Q.front) return false; //队空报错
x = Q.data[Q.front];
return true;
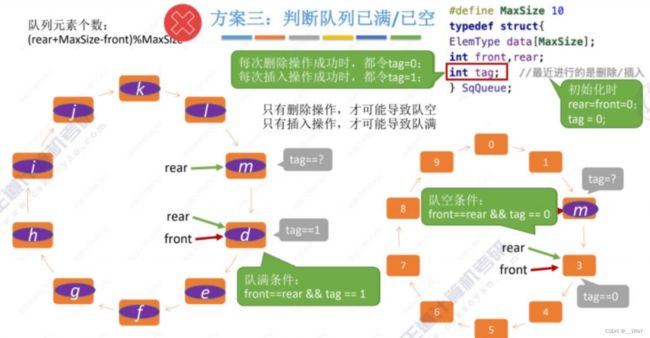
}队列元素个数：length = (rear + maxsize - front）%maxsize
判空判满的再思考？？？（命题：不可浪费存储单元时，如何判空判满？下面给出两种不浪费存储空间的方案（辅助变量法）——size法 和 tag法）
size法：
tag法：
关于队尾指针指向哪里的再思考？？？（如果队尾指针并不是指向队尾的后一个空位置，而是直接指向队尾元素，初始化、入队、出队操作会有变化）
2.3小结
| 比较项 | rear指向队尾下一个 | rear指向队尾 | |||||
| 初始化 | 牺牲存储空间法 | rear = front =0 |  |
front = 0；rear = maxsize-1 |  |
||
| 辅助变量法 | size法 | rear = front =0；size =0（入队size++，出队size--） | front = 0；rear = maxsize-1;size =0（入队size++，出队size--） | ||||
| tag法 | rear = front =0；tag = 0（入队tag=1，出队tag=0） | front = 0；rear = maxsize-1；tag = 0（入队tag=1，出队tag=0） | |||||
| 判空 | 牺牲存储空间法 | rear == front |  |
(rear+1)%maxsize == front |  |
||
| 辅助变量法 | size法 | front ==rear && size == 0 |  |
(rear+1)%maxsize == front && size == 0 | |||
| tag法 | front ==rear && tag == 0 |  |
(rear+1)%maxsize == front && tag == 0 | ||||
| 判满 | 牺牲存储空间法 | （rear+1）%maxsize == front |  |
（rear+2）%maxsize == front |  |
||
| 辅助变量法 | size法 | front ==rear && size == maxsize |  |
（rear+2）%maxsize == front && size == maxsize | |||
| tag法 | front ==rear && tag == 1 |  |
（rear+2）%maxsize == front && tag == 1 | ||||
| 入队 | 先赋值再移针 Q.data[Q.rear] = x; Q.rear = (Q.rear+1)%maxsize; |
先移针再赋值 Q.rear = (Q.rear+1)%maxsize; Q.data[Q.rear] = x; |
|||||
| 出队 | 都是先出队再移针 x = Q.data[front]; Q.front =(Q.front+1)%maxsize; |
||||||
2.3队列的链式存储实现
链式队列：逻辑结构——线性结构；存储结构（物理结构）——顺序存储
链式队列的定义：
typedef struct LinkNode{ //链式队列节点
ElemType data;
struct LinkNode *next;
}LinkNode;
typedef struct{ //链式队列
LinkNode *front,*rear; //队列的队头队尾指针
}LinkQueue; 
基本操作：
链式队列的初始化（创）：
//带头结点
//初始化（创）
void InitLinkQueue(LinkQueue &Q){
Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode)); //front rear都指向头节点
Q.front = NULL;
}
//判空
bool IsEmpty(LinkQueue Q){
if(Q.front == Q.rear) return true; //或者 if(Q.front == NULL) return true;
else return false;
}
//不带头节点
//初始化（创）
void InitLinkQueue(LinkQueue &Q){
Q.rear = NULL; //初始时front rear 都指向NULL
Q.front = NULL;
}
//判空
bool IsEmpty(LinkQueue Q){
if(Q.front == NULL) return true;
else return false;
} 链式队列的入队操作（增）：
//带头结点
void EnQueue(LinkQueue &Q,ElemType x){ //x入队 ，尾节点的后插操作
LinkNode *s = (LinkNode*)malloc(sizeof(LinkNode)); //为新入队元素申请一块空间
s->data = x;
s->next = NULL; //启后
Q->rear->next = s; //承前
Q->rear = s; //rear指向新的队尾
}
//不带头节点
void EnQueue(LinkQueue &Q,ElemType x){
LinkNode *s = (LinkNode*)malloc(sizeof(LinkNode)); //为新入队元素申请一块空间
s->data = x;
s->next = NULL; //启后
if(Q.front == NULL) { //空队列时，特殊处理——front rear都指向新插入的第一个节点
Q.front = s;
Q.rear = s;
}else{ //非空队列时，则是一般的队尾后插操作
Q->rear->next = s; //承前
Q->rear = s; //rear指向新的队尾
}
}
链式队列的出队操作（删）：
//带头节点
bool DeQueue(LinkQueue &Q,ElemType &x) {//队头出队， 并用x代回
if (Q.front == NULL) return false; //队空
LinkNode *p = Q.front->next; //头节点后第一个元素即为队头
x = p->data;
Q.front->next = p->next; //修改队头
if(p == Q.rear) Q.rear = Q.front; //若所删除的p正好是队尾元素，则删除后要修改rear，使队置空
free(p);
return true;
}
//不带头节点
bool DeQueue(LinkQueue &Q,ElemType &x) {//队头出队， 并用x代回
if (Q.front == NULL) return false; //队空
LinkNode *p = Q.front; //第一个元素即为队头
x = p->data;
Q.front = p->next; //修改队头
if(p == Q.rear){
Q.rear = Q.front =NULL; //若所删除的p正好是队尾元素，则删除后要修改rear，使队置空
}
free(p);
return true;
}
增删注意：注意第一个元素入队和最后一个元素出队时，要特殊处理。
获取链式队列对头操作（查）：获取队头元素
带头结点：Q.front->next是队头
不带头节点：Q.front是队头
链式队列的判满操作：
链式队列一般不会队满，除非内存不足。
顺序存储：预分配的空间耗尽时则满。
队长的计算：从头遍历O(n)，若经常用到队长这个变量，可以在定义时，增加int length变量记录队长。——按需灵活定义数据结构
2.4双端队列
双端队列：允许从两端插入/删除的线性表。
队列：允许从一端插入、一端删除的线性表。
栈：允许从一端插入/删除的线性表。
两种变种：
考点：判断输出序列是否合法
栈的合法->双端队列合法
2.5队列的应用
1.树的层次遍历（详见“树”章节）
树的层次遍历：遍历树的各个节点
思路：子节点入队，父节点出队
2.图的广度优先遍历（详见“图”章节）
思路：节点A的未被访问过的邻接节点入队后，节点A出队
3.队列在操作系统中的应用
FCFS(First Come First Service，先来先服务）策略——有限的系统资源的分配；
打印数据缓冲区(FIFO)；
3.特殊矩阵的压缩存储
3.1数组的存储结构
一维数组
二维数组
3.2特殊矩阵
普通矩阵
对称矩阵
三角矩阵
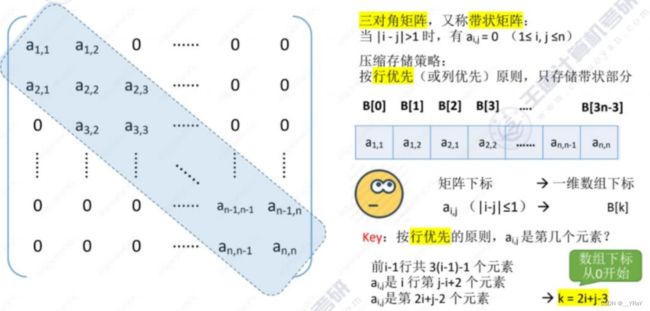
三对角矩阵
稀疏矩阵
