Lab1 datalab

修改bits.c，使其满足btest的测试，代码规范./dlc bits.c
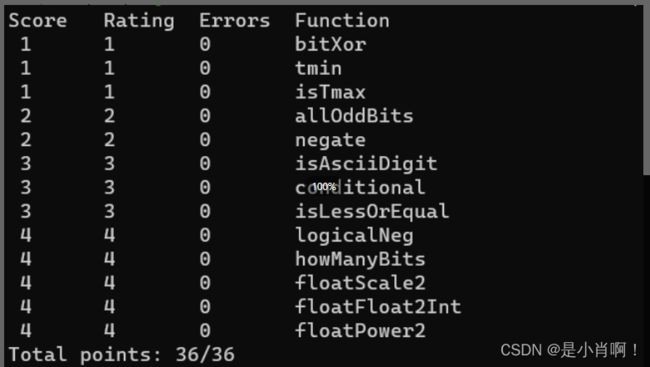
测试

1. make clean
2. make btest
3. ./btest

bitXor

思路

1. 题目的意思是用按位&和取反~实现异或^操作。
2. 即x和y的同一位置如果都是1或者都是0，那么异或之后是0，否则是1
   1. x & y的结果的某一位为1，代表x和y的这一位都是1。而如果x和y的某一位都是1，那么经过异或操作时候，这一位应该是0，所以对这个结果取反，得到a。a的二进制表示中，每一个0都代表这个位置的x和y都是1。
   2. 刚刚处理了x和y同一位置都是1，现在应该处理两个位置都是0。可以通过先分别对x和y取反，将这个问题又转为处理同一位置为1。通过和上一步一样的操作，可以得到b。
   3. a和b的二进制表示中，每一个0都代表x和y在这个位置同时是0或者同时是1。那么将a&b就得到了异或的结果，即相同为0，不同为1。

/*
 * bitXor - x^y using only ~ and &
 *   Example: bitXor(4, 5) = 1
 *   Legal ops: ~ &
 *   Max ops: 14
 *   Rating: 1
 */
int bitXor(int x, int y) {
  // 两个1的位置是0，否则是1
  int a = ~(x & y);
  // 两个0的位置是0，否则是1
  int b = ~(~x & ~y);
  // 因此将a和b按位&之后，两个1或者两个0的位置都是0，其他位置是1
  return a & b;
}

tmin

思路

1. 送分题

/*
 * tmin - return minimum two's complement integer
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void) { return 1 << 31; }

isTmax

思路

1. 验证x是不是最大的有符号整数，最大的有符号整数应该是0x7fffffff，记为tmax
2. 如果只能用位运算，那么要尽量将操作的数往0或者0xffffffff上靠，可以发现tmax+tmax+1正好就是0xffffffff。拿到了0xffffffff，那就好办了，对它取反，正好得到0，也就是下面代码里的b
3. 那么是不是只有tmax可以通过~(x+x+1)的操作得到0呢，不是！0xffffffff也是可以得到0的。因此还需要对它进行特判。它加上1或者取反正好就是0,再取个非，刚好就是1，也就是下面代码里的c。
4. 综上所述，b为0，并且c也等于0，才能够证明x是Tmax
   易错点
5. 这一题相当于是根据Tmax的特点进行一些操作，得到一个只有Tmax才能经过这一系列操作得到的值。但是还有一个边界情况那就是0xffffffff需要特判。写代码的时候要小心这些corn case

/*
 * isTmax - returns 1 if x is the maximum, two's complement number,
 *     and 0 otherwise
 *   Legal ops: ! ~ & ^ | +
 *   Max ops: 10
 *   Rating: 1
 */
int isTmax(int x) {
  // 0xffffffff，这一步不能用异或
  int a = x + x + 1;
  // 0x00000000，如果b为0，那么b要么是0x3fffffff，要么是0xffffffff
  int b = ~a;
  // 排除x为0xffffffff，如果x是0xffffffff，那么c就是1，否则c就是0
  int c = !(x + 1);
  // 只有b和c都是0，才返回1
  return !(b | c);
}

allOddBits

思路

1. 这一题要判断这个数是否满足：所有的奇数位都是1
2. 那么可以通过0xAAAAAAAA这个数与x进行按位与，将取出所有的奇数位，并将偶数为置0
3. 如果这个数所有奇数位都是1，那么它现在应该和0xAAAAAAAA相同。相同的话异或为0，再取个反，刚好是1。

/*
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   where bits are numbered from 0 (least significant) to 31 (most significant)
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x) {
  // 构造出奇数位均为1的数
  int a = (0xaa << 24) + (0xaa << 16) + (0xaa << 8) + 0xaa;
  // 将a看做掩码，取出x中所有奇数位
  int b = x & a;
  // 判断a和b是否相同，只有当a和b相同，异或才为0，那么取！后才为1
  return !(a ^ b);
}

negate

思路

1. 送分题，按位取反，末位加1

/*
 * negate - return -x
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x) { return (~x) + 1; }

isAsciiDigit

思路

1. 判断这个数是否在$0x30<=x<=0x39$这个范围内
2. 这个范围可以写成十六进制，即
   1. 0x 0011 0000
   2. 0x 0011 1001
3. 可以发现，高28位一定是0x0000003，低4位则在0x0到0x9之间。
   1. 所以先将高28位取出来，判断是否是0x0000003
   2. 再将低4位取出来
      1. 低4位里，如果第4位是0，那么对低三位则没有要求
      2. 如果第4位是1，那么第二位和第三位一定是0，对低1位没有要求

/*
 * isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0'
 * to '9') Example: isAsciiDigit(0x35) = 1. isAsciiDigit(0x3a) = 0.
 *            isAsciiDigit(0x05) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 3
 */
int isAsciiDigit(int x) {
  // 0x 0011 0000
  // 0x 0011 1001
  // 首先，右移4位之后，应该是0x3，即a=1
  int a = !((x >> 4) ^ (0x3));
  // 低4位，要么第4位为0，要么就只能是1001或者1000
  // b为1，代表第4位为0
  int b = !((x >> 3) & 1);
  // c为1，代表为1001或者1000，即第1位和第4位无所谓，但是第2和第3位必须是0
  int c = !(x & 0x6);
  // printf("-----------------\n%x\n%d\n%d\n%d\n%d\n",x,a,b,c,a&(b|c));
  return a & (b | c);
}

conditional

思路

1. 实现三目运算符
2. 主要是看x，如果x不为0，那么返回y，如果x为0，那么返回z。
3. 这个做法就有点tricky
   1. 如果x不为0，那么将x变为0xffffffff
   2. 如果x为0，那么将x变为0
   3. 在上面改变的基础上，
      1. 如果x不为0，那么应该返回y，此时的x经过变换之后是全1
         1. 将x和y按位与，按位与的结果就是y
         2. 将~x和z按位与，按位与的结果是0
         3. 将上述两个结果进行按位或操作，得到的就是y
      2. 之所以使用按位或操作，是因为如果x为0，依然可以返回正确结果。此时x和y按位与就是0，~x和z按位与的结果就是z，按位或之后的结果就是z
      3. 如何将非0的x变为全1呢？首先通过两次！操作，可以把非零的x变为1，此时对它取反再加1就是全1了

/*
 * conditional - same as x ? y : z
 *   Example: conditional(2,4,5) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 16
 *   Rating: 3
 */
int conditional(int x, int y, int z) {
  // 如果x不为0，则得到一个全1的数，如果x为0，则得到一个全0的数
  // 如果x为0，则得到0，如果x非0，则得到1
  int a = !!x;
  // 如果a为0，则b为0，如果a为1，则b为-1，即全1
  int b = ~a + 1;
  // c和d一定有一个为0
  int c = b & y;
  int d = ~b & z;
  return c | d;
}

isLessOrEqual

思路

1. 判断x是否小于等于y
2. 如果x和y符号不同
   1. 如果x为负数，则小于y
   2. 如果x为正数，则大于y
3. 如果x和y符号相同，则需要计算x和y的差值，因为不可以直接用减号，计算x-y，其实就是计算x+（y的补码）
   1. 如果差值小于0，则小于y
   2. 如果差值大于0，则大于y
4. 还需要特判一下x是否等于y

/*
 * isLessOrEqual - if x <= y  then return 1, else return 0
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y) {
  // 如果符号不同，则正数更大，如果符号相同，则看差值，还要特判一下x是否和y相同
  int x_flag = x >> 31 & 1;
  int y_flag = y >> 31 & 1;
  // 如果flag_not_same为1，则代表符号不同，如果为0，则代表符号相同
  int flag_not_same = x_flag ^ y_flag;
  // 还要结合差值的正负来看,x-y，即x+(y的补码)
  int y_ = ~y + 1;
  int sub_flag = (x + y_) >> 31 & 1;
  // 如果符号不同并且x为负，即a=1，即x_flag=1，并且flag_not_same=1，
  int a = flag_not_same & x_flag;
  // 如果符号相同，并且差值为负，即b=1，即flag_same=0,sub_flag=1;
  int b = !(flag_not_same | (!sub_flag));
  // 如果两个数相同，则c为1，否则c为0
  int c = !(x ^ y);
  return a | b | c;
}

logicalNeg

思路

1. 对于0，返回1，对于非0的数，返回0
2. 其实只需要对确定x是0后返回1，其他情况都是返回0
3. 做法很tricky
   1. 首先，对于任何符号位为0的数，加上Tmax之后，只有0不会导致溢出为负数。
   2. 因此只需要满足下面两个条件就可以返回1，否则返回0
      1. x的符号位是0
      2. x+Tmax之后的符号位也是0

/*
 * logicalNeg - implement the ! operator, using all of
 *              the legal operators except !
 *   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4
 */
int logicalNeg(int x) {
  // 先得到最大的32位有符号数
  int T_max = ~(1 << 31);
  // 得到x的符号
  int x_sign = x >> 31 & 1;
  // 将x和T_max相加，除了0，其他的数加上去之后一定是一个负数
  int a = x + T_max;
  int a_sign = a >> 31 & 1;
  // 只有当x和a的sign都是0时，才返回1，否则返回0
  return (x_sign ^ 1) & (a_sign ^ 1);
}

howManyBits

思路

1. 如果用补码来表示x，最少需要多少位？
2. 首先对于正数，符号位一定是0，因此只需要找到最高位的1
3. 其次对于负数，符号位一定是1，需要找到最高位的0，因为高位连续多个1其实就相当于一个1。为了方便起见，将负数取反，那么就和正数一样变成求最高位的1的问题。
4. 如何求最高位的1？使用二分的思想
   1. 首先判断高16位是否全0
      1. 如果不是全0，那么低16位肯定是需要的，将16加到答案里去，再右移16位，接下来再去处理高16位
      2. 如果是全0，那么低16不一定需要，不用加到答案里去。接下来继续处理低16位
   2. 接下来就是判断当前的8位。
      1. 注意了，这里的8位有可能是原来的八位，也有可能是高16位经过右移之后变成了新的低16位的八位！
   3. 然后就是不断的二分下去，直到只剩下一位
   4. 如果这一位是1，说明还需要1位。如果为0，则说明这一位不需要了。

/* howManyBits - return the minimum number of bits required to represent x in
 *             two's complement
 *  Examples: howManyBits(12) = 5
 *            howManyBits(298) = 10
 *            howManyBits(-5) = 4
 *            howManyBits(0)  = 1
 *            howManyBits(-1) = 1
 *            howManyBits(0x80000000) = 32
 *  Legal ops: ! ~ & ^ | + << >>
 *  Max ops: 90
 *  Rating: 4
 */
int howManyBits(int x) {
  // 如果是正数，那么直接求x的最高位1，如果是负数，则是要求最高位的0
  // 假设这个最高位为第x位，则答案案为x+1位，因为正数需要加上符号0，负数需要加上符号1
  // 对于负数，先预处理，将所有的1变成0，所有的0变成1
  // 如果x为正数，则help为0，如果x为负数，则help为0xffffffff
  int ans = 0;
  int help = x >> 31;
  // 通过help将x的1变成0,0变成1。若help为0，则x不变，若help为全1，则完成转换的任务
  x = x ^ help;
  // 下面就统一为了计算最高位的1所在的位置
  // 如果高16位不为0，则has_high_16为1，否则为0
  int has_high_16 = !!(x >> 16);
  // 如果高16位存在，即has_high_16为1，那么说明低16位肯定跑不掉了，正好就是has_high_16<<4
  // 如果高16位不存在，has_high_16为0，低16位就不一定都要，此时左移4位正好是0
  int add_bits = has_high_16 << 4;
  ans += add_bits;
  // 又是一个很巧妙的操作，如果add_bits不为0，说明低16位肯定是需要的，那么就不用管低16位，直接移位
  // 如果add__bits为0，说明高16位肯定不需要，低16位可能需要，那么此时右移0位，接下来正常处理低16位
  x >>= add_bits;

  int has_high_8 = !!(x >> 8);
  add_bits = has_high_8 << 3;
  ans += add_bits;
  x >>= add_bits;

  int has_high_4 = !!(x >> 4);
  add_bits = has_high_4 << 2;
  ans += add_bits;
  x >>= add_bits;

  int has_high_2 = !!(x >> 2);
  add_bits = has_high_2 << 1;
  ans += add_bits;
  x >>= add_bits;

  int has_high_1 = !!(x >> 1);
  add_bits = has_high_1 << 0;
  ans += add_bits;
  x >>= add_bits;

  // x可能现在是1
  ans += x;

  return ans + 1;
}

floatScale2

思路

1. 将一个浮点数乘2，这个浮点数以无符号整数的形式给出
2. uf是NaN一类指数为11111111的，直接返回
3. uf是非规格化数，直接将小数部分乘2
4. uf是规格化数，将指数加1就可以完成乘2的效果了

/*
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf) {
  // 分别取出符号，指数，以及有效数位，
  // 其中有效的取出比较tricky，是对sign和e的对应位置进行异或，即将高9位都置为0，剩下的就是有效数位了
  unsigned sign = (uf >> 31) & 1;
  unsigned e = (uf >> 23) & 0xff;
  unsigned f = uf ^ (sign << 31) ^ (e << 23);
  // 如果uf为NaN等特殊值，即指数为全1，直接返回这个特殊值本身
  if (!(e ^ 0xff)) {
    return uf;
  }
  // 如果uf为非规格化的数，即指数为0，直接将f*2即可
  // 这里感觉有点问题，如果这个非规格数*2后达到了规格数的范围了，是不是要额外处理？
  if (!e) {
    return (sign << 31) | (f << 1);
  }
  // 如果uf为规格化的数
  return (sign << 31) | ((e + 1) << 23) | (f);
}

floatFloat2Int

思路

1. 将浮点数转为整数
2. 如果这个浮点数超出了int的范围，直接返回0x80000000
3. 如果这个浮点数的阶数小于0，说明还需要将小数部分除一个2的倍数，在int里肯定直接化为0了，因此直接返回0
4. 否则的话，按具体情况对小数部分进行移位运算
   1. 这里虽然叫小数部分，但是其实因为这个float类型的变量是用int类型给出的，因此这里的小数部分已经是默认左移23位的了。需要考虑这个因素。

/*
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf) {
  // 分别取出符号，指数，以及有效数位，
  // 其中有效位的取出比较tricky，是对sign和e的对应位置进行异或，即将高9位都置为0，剩下的就是有效数位了
  unsigned sign = (uf >> 31) & 1;
  unsigned e = (uf >> 23) & 0xff;
  unsigned f = uf ^ (sign << 31) ^ (e << 23);
  // 如果指数大于等于31了，因为要返回的值是int类型，1<<31位直接爆int了，所以返回0x80000000u
  int E = e - 127;
  if (E >= 31) {
    return 0x80000000;
  }
  // 如果指数小于0了，那么肯定是返回0，因为需要对小数部分除2，那么对int来说，就是0
  if (E < 0) {
    return 0;
  }
  // 真正的小数部分，是有一个隐藏的1在最前面的，这里不用考虑非规格化数，因为它已经在前面的E<0里给淘汰了
  int frac = f | 0x800000;
  // 这个小数部分是用整数来表示的，即默认左移了23位，那么当前的移位应该减去23
  int real_f = (E > 23) ? (frac << (E - 23)) : (frac >> (23 - E));
  return sign ? -real_f : real_f;
}

floatPower2

思路

1. 将$2^x$用浮点数表示
2. 符号位和小数部分一定是纯0，因此只需要考虑阶码
3. 如果阶码小于等于0，直接return 0
4. 如果阶码超过了0xff，return INF，即0x7f800000
5. 如果正常的话，直接将阶码左移23位就得到这个浮点数了

/*
 * floatPower2 - Return bit-level equivalent of the expression 2.0^x
 *   (2.0 raised to the power x) for any 32-bit integer x.
 *
 *   The unsigned value that is returned should have the identical bit
 *   representation as the single-precision floating-point number 2.0^x.
 *   If the result is too small to be represented as a denorm, return
 *   0. If too large, return +INF.
 *
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatPower2(int x) {
  // 得到阶码
  int e = x + 127;
  // 非规格数，直接返回0
  if (e <= 0) {
    return 0;
  }
  // 无穷
  if (e >= 0xff) {
    return 0x7f800000;
  }
  // 规格数，符号位0，小数部分也是0
  return e << 23;
}