Leetcode 329. Longest Increasing Path in a Matrix (python+cpp)

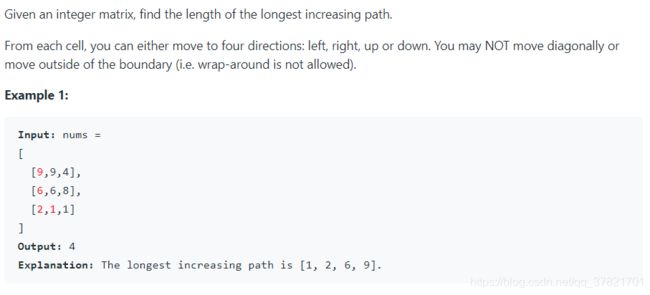
题目

解法1：dfs暴力

class Solution:
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        def dfs(i,j,prev):
            if i<0 or i>=m or j<0 or j>=n or matrix[i][j]<=prev:
                return 0
            #print(i,j)
            tmp = 0
            tmp = max(dfs(i+1,j,matrix[i][j]),dfs(i,j+1,matrix[i][j]),dfs(i-1,j,matrix[i][j]),dfs(i,j-1,matrix[i][j])) + 1
            return tmp
        
        if not matrix or not matrix[0]:
            return 0
        
        m,n = len(matrix),len(matrix[0])
        #dfs(0,1,float('-inf'))
        ans = 0
        for i in range(m):
            for j in range(n):
                print((i,j),dfs(i,j,float('-inf')))
                ans = max(dfs(i,j,float('-inf')),ans)
        
        return ans

解法2：dfs+memorization

class Solution:
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        def dfs(i,j,prev):
            if i<0 or i>=m or j<0 or j>=n or matrix[i][j]<=prev:
                return 0
            if memo[i][j] != float('-inf'):
                return memo[i][j]
            memo[i][j] = max(dfs(i+1,j,matrix[i][j]),dfs(i,j+1,matrix[i][j]),dfs(i-1,j,matrix[i][j]),dfs(i,j-1,matrix[i][j])) + 1
            return memo[i][j]
        
        if not matrix or not matrix[0]:
            return 0
        
        m,n = len(matrix),len(matrix[0])
        ans = 0
        memo = [[float('-inf')]*n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                ans = max(dfs(i,j,float('-inf')),ans)
        
        return ans

C++版本：

class Solution {
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int ans = 0;
        int m = matrix.size(), n = matrix[0].size();
        vector<vector<int>> memo(m,vector<int>(n,-INT_MAX));
        for (int i=0;i<matrix.size();i++){
            for (int j=0;j<matrix[0].size();j++){
                ans = max(ans,dfs(i,j,-INT_MAX,memo,matrix));
            }
        }
        return ans;
    }
    int dfs(int i, int j, int prev, vector<vector<int>>& memo, vector<vector<int>>& matrix){
        if (i<0 || i>=matrix.size() || j<0 || j>=matrix[0].size() || matrix[i][j]<=prev) {
            return 0;
        }
        if (memo[i][j] != -INT_MAX) return memo[i][j];
        memo[i][j] = max(dfs(i+1,j,matrix[i][j],memo,matrix)+1,memo[i][j]);
        memo[i][j] = max(dfs(i,j+1,matrix[i][j],memo,matrix)+1,memo[i][j]);
        memo[i][j] = max(dfs(i-1,j,matrix[i][j],memo,matrix)+1,memo[i][j]);
        memo[i][j] = max(dfs(i,j-1,matrix[i][j],memo,matrix)+1,memo[i][j]);
        return memo[i][j];
        
    }
};

解法3：dp+topology sort

分三步：

• 建图
• 获取拓扑序
• 根据拓扑序进行dp
  dp状态转移方程为：dp[A[i]] = max(dpA[j]+1)，A[i]为节点标号，A[j]为指向A[i]节点的所有节点标号，i，j代表节点在拓扑序中的下标位置
  其实广义的dp就是根据拓扑序来转移状态的，只是平常大部分dp的顺序都显而易见，而这边需要手动找到拓扑序

宏观上理解这种解法：拓扑排序是为了保证我们dp的子问题已经被计算。举个例子

class Solution:
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        if not matrix or not matrix[0]: 
            return 0
        
        # construct graph
        graph = collections.defaultdict(list)
        m,n = len(matrix),len(matrix[0])
        indegrees = [[0]*n for _ in range(m)]
        dirs = [[-1,0],[1,0],[0,1],[0,-1]]
        for i in range(m):
            for j in range(n):
                for d in dirs:
                    x = i+d[0]
                    y = j+d[1]
                    if 0<=x<m and 0<=y<n and matrix[i][j]<matrix[x][y]:
                        graph[(x,y)].append((i,j))
                        indegrees[i][j] += 1
        
        # topology sort
        q = collections.deque()
        for i in range(m):
            for j in range(n):
                if indegrees[i][j] == 0:
                    q.append((i,j))
        
        order = []
        while q:
            i,j = q.popleft()
            order.append((i,j))
            for x,y in graph[(i,j)]:
                indegrees[x][y] -= 1
                if indegrees[x][y] == 0:
                    q.append((x,y))
        # dynamic programming according to topology order
        dp = [[1]*n for _ in range(m)]
        for i in range(m*n-1,-1,-1):
            x,y = order[i][0],order[i][1]
            for x1,y1 in graph[(x,y)]:
                dp[x][y] = max(dp[x][y],(dp[x1][y1]+1))
        ans = 0
        for row in dp:
            for num in row:
                ans = max(ans,num)
        return ans

其实用拓扑排序并不需要后面的dp，这是一个Longest path in a DAG的问题，参考这边：https://www.geeksforgeeks.org/find-longest-path-directed-acyclic-graph/

class Solution {
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        vector<vector<int>> indegrees(m,vector<int>(n,0));
        vector<pair<int,int>> dirs{{0,1},{0,-1},{1,0},{-1,0}};
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                for(auto& d : dirs){
                    int x = i+d.first;
                    int y = j+d.second;
                    if(x < 0 || y < 0 || x >= m || y >= n) continue;
                    if(matrix[i][j] > matrix[x][y]){
                        indegrees[i][j]++;
                    }
                }
            }
        }
        queue<pair<int,int>> q;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(indegrees[i][j] == 0) q.push(make_pair(i,j));
            }
        }
        int lenth = 0;
        while(!q.empty()){
            int size = q.size();
            for(int i=0;i<size;i++){
                auto curr = q.front();
                q.pop();
                for(auto& d : dirs){
                    int x = curr.first + d.first;
                    int y = curr.second + d.second;
                    if(x < 0 || y < 0 || x >= m || y >= n) continue;
                    if(matrix[x][y] > matrix[curr.first][curr.second]){
                        indegrees[x][y]--;
                        if(indegrees[x][y] == 0) q.push(make_pair(x,y));
                    }
                }
            }
            lenth++;
        }
        return lenth;
    }
};