论文笔记——Influence Maximization in Undirected Networks
Influence Maximization in Undirected Networks
- Contribution
- Motivation
- Preliminaries
-
- Notations
- Main results
-
- Reduction to Balanced Optimal Instances
- Proving Theorem 3.1 for Balanced Optimal Instances
Contribution
好久没发paper笔记了,这篇比较偏理论,可能边看边记比较高效一些,仅作为个人笔记,如有解读不到的还请包涵。这篇paper的贡献有两个,首先是证明了在无向图中使用greedy可以突破 1 − 1 / e 1-1/e 1−1/e的barrier(也就是greedy在无向图上会更强),达到 1 − 1 / e + c 1-1/e+c 1−1/e+c的近似,其中 c c c为常数;其次,该论文证明了无向图上的influence maximization是 A P X − h a r d APX-hard APX−hard。
Motivation
作者先给了一个比较紧的例子:
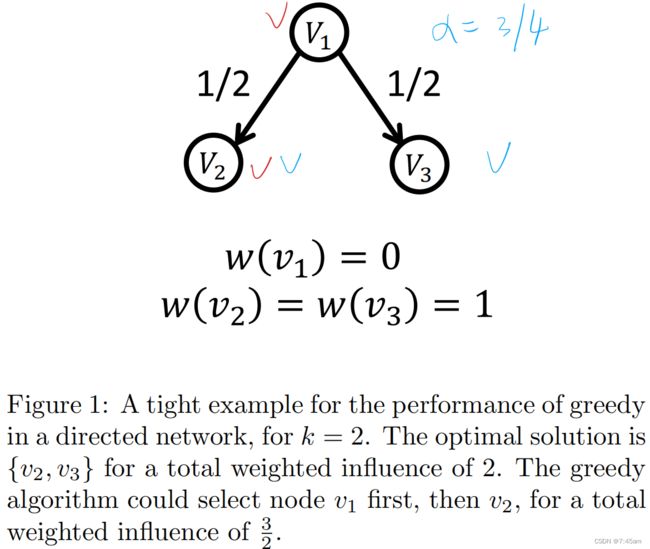
这里蓝色为OPT(optimal,最优解),红色为 G R D GRD GRD(greedy算法选择的种子节点)。注意,有向图中greedy选择 v 1 , v 2 v_1,v_2 v1,v2是因为 v a l ( v 1 ) = v a l ( v 2 ) = v a l ( v 3 ) = 1 val(v_1)=val(v_2)=val(v_3)=1 val(v1)=val(v2)=val(v3)=1。然而在无向图中,情况会更不一样:

这里 v a l val val为节点的影响力,同样,这里 O P T = { v 2 , v 3 } OPT = \{v_2,v_3\} OPT={v2,v3}(因为 v 2 , v 3 v_2,v_3 v2,v3的权重大),这里依然有 v a l ( { v 2 , v 3 } ) = 2 val(\{v_2,v_3\})=2 val({v2,v3})=2。然而贪心算法会可能会选择 G R D = { v 1 , v 2 } GRD = \{v_1,v_2\} GRD={v1,v2},且有 v a l ( v 2 ) = v a l ( v 3 ) = 1 + 0 + 1 ∗ 1 / 2 ∗ 1 / 2 = 5 / 4 val(v_2) =val(v_3) = 1 + 0 + 1 * 1/2 * 1/2 = 5/4 val(v2)=val(v3)=1+0+1∗1/2∗1/2=5/4,那么根据Greedy的习惯, G R D = { v 2 , v 3 } GRD = \{v_2,v_3\} GRD={v2,v3},也就是说,在这个例子中,greedy会选出最优解。
同样的结构,greedy在无向图和有向图上的表现却大相径庭,背后原因令人暖心:在无向图中,greedy选出的节点的影响力会和OPT的影响力重叠更少。然而这只是一个例子,不具备代表性,为了generalize这一现象,作者将使用 XYZ \textit{XYZ} XYZ lemma来构建反例(如下图)来说明在无向图中, k = 1 k=1 k=1时,greedy算法带来的近似比可以任意接近 3 / 4 3/4 3/4; k k k变大时,近似比则可以任意接近 1 − 1 / e 1-1/e 1−1/e。
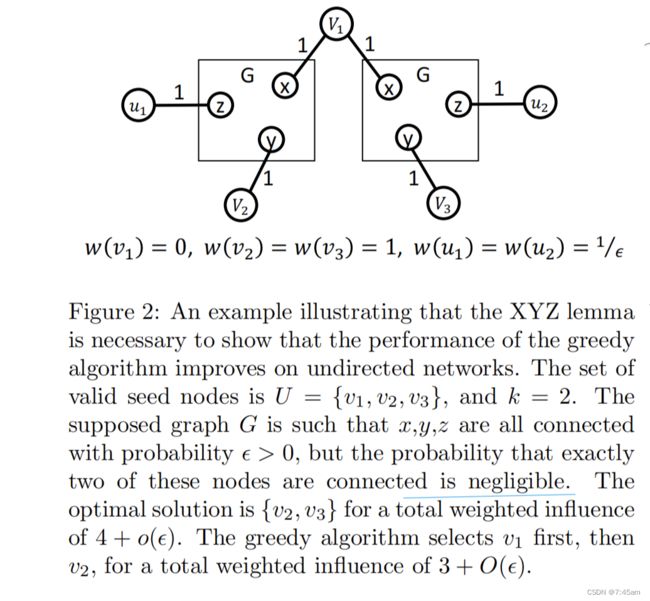
作者的整体思路分三步走:
- Counter Example :首先构建worst case “balanced OPT”。在这个case中greedy算法的影响力函数 v a l ( . ) val(.) val(.)几乎是线性的,且每个OPT中的节点的影响力几乎是一样的。在这种情况下,greedy的近似比是 1 − 1 / e 1-1/e 1−1/e;除此之外,greedy的近似比都大于 1 − 1 / e 1-1/e 1−1/e。
- Linearity:在无向图中考虑 v a l ( . ) val(.) val(.)函数的线性情况。这里指的是,无向图中的OPT中的元素必须尽可能的不处在同一个连通分量中: v a l ( O P T ) − v a l ( O P T ∖ o i ) > v a l ( o i ) val(OPT) - val(OPT \setminus {o_i}) > val(o_i) val(OPT)−val(OPT∖oi)>val(oi),即节点 o i o_i oi的增益大于其本身的影响力。这对greedy有很大的影响。
- Technical part:设 S S S为 O P T OPT OPT中前 k / 4 k/4 k/4个种子,考虑greedy选择剩余的种子的情况:作者证明了要么greedy会选择具有较大增益的点,达到 1 − 1 / e + c 1-1/e+c 1−1/e+c的近似;要么就是在balanced form情况下,OPT会导致矛盾。这里矛盾的点在于:在balance form时,greedy在选完前 4 / k 4/k 4/k个种子后,接着应该继续选具有最大增益的点(Lemma 4.2),否则就不会具有比 1 − 1 / e 1-1/e 1−1/e更好的近似比;换句话说,假设greedy不能提供更好的近似比,那么应该选出增益低的节点,但是由于 M ′ M' M′(后续会讲到)中的节点是 5 ϵ 5\epsilon 5ϵ-uniform的,和 S S S在一个连通分量中的概率会很低,因此要选一个 O i ∈ M ′ O_i\in M' Oi∈M′具有低增益是不可能的,因为增益迪就说明 O i O_i Oi和S在同一个连通分量里面。证明的过程用到了一些technical的概率分析,描述了 XYZ \textit{XYZ} XYZ Lemma。
Preliminaries
Notations
| notations | Meaning |
|---|---|
| < G ( V , E ) , U , p , w , k > |
An undirected graph |
| U | a valid seed set |
| p p p | he probability in edges |
| w w w | the weight on node |
| k k k | an integer |
| H ( V ′ , E ′ ) H(V',E') H(V′,E′) | an live-edge graph of G G G |
| v a l ( S ∣ T ) val(S|T) val(S∣T) | v a l ( S ∪ T ) − v a l ( T ) val(S \cup T) - val(T) val(S∪T)−val(T) |
| S → T S \rightarrow T S→T | some vertices in S S S in the same component of T T T |
此外,这里作者提供了一个加权图和无权图互相转化的方法。故文章中提到的图都是无权图。
Main results
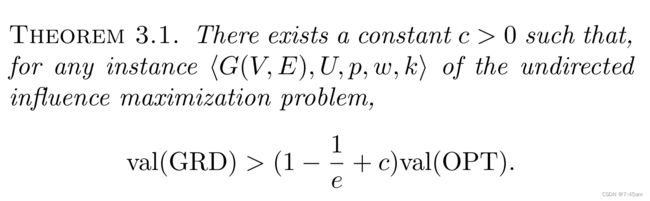
这也是这篇paper的主要贡献,接下来是定理3.1的证明,也就是文章中具有technical的部分。首先构建lemma 3.1和lemma 3.2,这两个lemma想做的事情是说,当OPT不是特定的"balance"形式的时候,定理3.1是成立的。这里的“balance”其实就是worst case。
Reduction to Balanced Optimal Instances
首先定义了归一化影响力,具体定义如下。这个式子衡量了 X X X中节点的平均影响力和OPT中总体节点影响力的比值。 ρ ( x ) > 1 \rho(x) >1 ρ(x)>1说明 X X X中节点的平均影响力比OPT的节点平均影响力。

给定 ϵ > 0 \epsilon > 0 ϵ>0,我们说一组节点 X X X是 ϵ \epsilon ϵ-uniform 的,若其每个不包含x节点的集合 X X X的元素的normalized influence浮动都很小,即 ( 1 − ϵ ) ≤ ρ ( x ∣ X ∖ x ) ≤ ( 1 + ϵ ) (1-\epsilon) \leq \rho(x \mid X \setminus {x}) \leq (1 + \epsilon) (1−ϵ)≤ρ(x∣X∖x)≤(1+ϵ),那么该组节点的发挥就很稳定,称之为 ϵ \epsilon ϵ-uniform。
X X X是 ϵ \epsilon ϵ-independent的:若每个节点和X中其他节点出现在同一连通分量的概率 P r [ x → X { x } ] ≤ ϵ Pr[x \rightarrow X\ \{x\}] \leq \epsilon Pr[x→X {x}]≤ϵ。
X X X是 ϵ \epsilon ϵ-balanced:同时满足 ϵ \epsilon ϵ-uniform和 ϵ \epsilon ϵ-independent,也就是说这组节点即均匀分布,又发挥稳定( v a l ( . ) val(.) val(.)几乎是线性的)。
这个章节的目的是想说明对于这样的一个 ϵ > 0 \epsilon > 0 ϵ>0,greedy要么可以实现一个 1 − 1 / e + f ( ϵ ) 1-1/e+f(\epsilon) 1−1/e+f(ϵ)的近似,要么OPT就是 ϵ \epsilon ϵ-balanced。
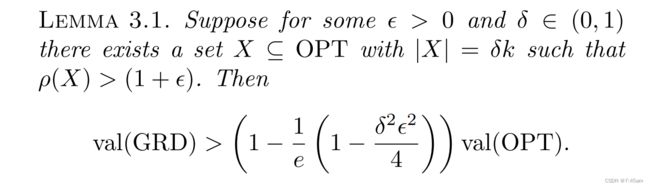
Lemma 3.1说明了greedy算法严格保证了一个大于 1 − 1 / e 1-1/e 1−1/e的近似比。证明如下:

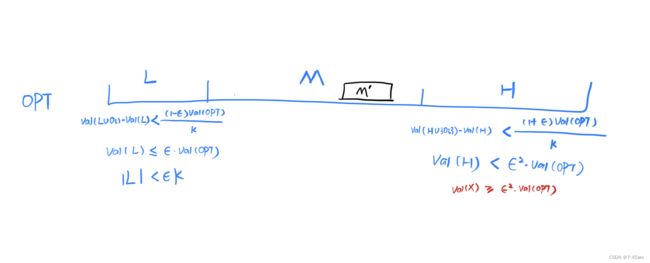
接下来的lemma说明,OPT一定满足下面两个条件之一:1、要么包含了一组 X X X,满足归一化后的X的影响力严格大于1且 v a l ( X ) = Ω ( v a l ( O P T ) ) val(X) = \Omega(val(OPT)) val(X)=Ω(val(OPT)),即 X X X的lower bound是 v a l ( O P T ) val(OPT) val(OPT);2、要么OPT可以根据条件划分为L,H,M。L的划分方法如下:

其实这里 L L L存放了一组点,满足 v a l ( L ) ≤ ϵ ⋅ v a l ( O P T ) val(L) \leq \epsilon \cdot val(OPT) val(L)≤ϵ⋅val(OPT),也就是将 o i o_i oi加入 Z Z Z(不包含 o i o_i oi)带来的收益小于 ( 1 − ϵ ) v a l ( O P T ) k \frac{(1-\epsilon)val(OPT)}{k} k(1−ϵ)val(OPT)的那部分点,这些点至少会有 ϵ ⋅ k \epsilon \cdot k ϵ⋅k个。对于剩下的 k − ϵ ⋅ k k - \epsilon \cdot k k−ϵ⋅k个点,我们将它划分到 X X X中。
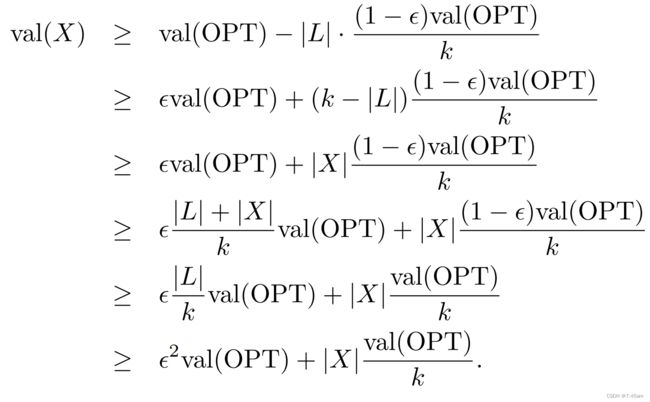
这样一来, ρ ( X ) > 1 \rho (X) >1 ρ(X)>1且 v a l ( X ) = Ω ( v a l ( O P T ) ) val(X) = \Omega(val(OPT)) val(X)=Ω(val(OPT))。
若 ∣ L ∣ ≤ ϵ ⋅ k \mid L \mid \leq \epsilon \cdot k ∣L∣≤ϵ⋅k,则不存在 X X X,那么继续划分。对于M和H,划分方法如下:

也就是说,在一个集合 Z = O 1 , . . . , O k Z = {O_1,...,O_k} Z=O1,...,Ok中,L是Z中一系列增益小于 ( 1 − ϵ ) v a l ( O P T ) k \frac{(1-\epsilon)val(OPT)}{k} k(1−ϵ)val(OPT)的节点,那么对于Z中剩下的点,选出前 j j j个连续增益最大的点 { O δ ( 1 ) , . . . , O δ ( j ) } \{O_{\delta(1)},...,O_{\delta(j)}\} {Oδ(1),...,Oδ(j)},若这些点的影响力大于 ϵ 2 v a l ( O P T ) \epsilon^2val(OPT) ϵ2val(OPT),则将其划分为X;否则为 H H H,剩下的点为 M M M。这波操作下来, L , H , M L,H,M L,H,M中的点都不会有normalized influence大于1的情况,也就是说,greedy在这种情况下不会出现比 1 − 1 / e 1-1/e 1−1/e好的近似比。根据划分的方法,满足lemma3.2中的条件:M是 ϵ \epsilon ϵ-uniform的。
证明如下:

接下来肯定是证明 ϵ \epsilon ϵ-independent了。但这里只证明 M M M中的部分。对于M,有:

也就是说, M ′ M' M′存在于 M M M中,且大小至少为 ∣ M ∣ − ϵ k \mid M\mid-\epsilon k ∣M∣−ϵk,且 M ′ M' M′中每个点 O i O_i Oi在 M ′ M' M′的连通分量中的概率最多为 5 ϵ 5\epsilon 5ϵ。这个证明暂且skip,没看懂。
Proving Theorem 3.1 for Balanced Optimal Instances
现在的情况是OPT被分成上面的样子了,这里 M ′ M' M′满足 5 ϵ 5\epsilon 5ϵ-independent和 ϵ \epsilon ϵ-uniform。按照之前的证明思路,若是有一个集合满足 ϵ \epsilon ϵ-balanced,那么该集合上的 v a l ( . ) 就是几乎就是线性的。接下来的证明策略如下。首先证明,给定 val(.)就是几乎就是线性的。接下来的证明策略如下。首先证明,给定 val(.)就是几乎就是线性的。接下来的证明策略如下。首先证明,给定S = {g_1,g_2,…,g_{k/4}}$,如果贪婪算法没有达到比 1 − 1 / e 1−1/e 1−1/e更好的近似, 那么每个 O i ∈ M ′ O_i\in M' Oi∈M′的边际影响一定不能太大(lemma 3.4),否则就会有greedy超过 1 − 1 / e 1-1/e 1−1/e的情况发生。
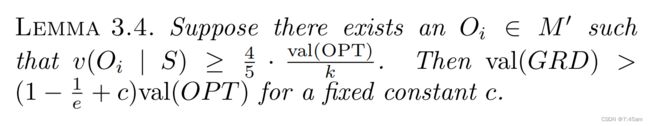

Lemma3.4描述了greedy选完前 k / 4 k/4 k/4之后依然还能选出增益大于 4 / 5 v a l ( O P T ) k 4/5 \frac{val(OPT)}{k} 4/5kval(OPT)的情况。接下来的Lemma 3.5会考虑矛盾的情况:当 M ′ M' M′中还存在更低的uniform集合。
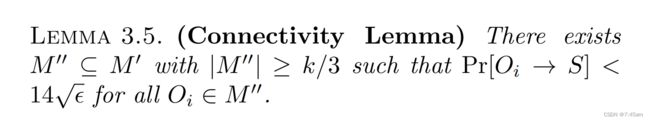
L e m m a 3.4 Lemma 3.4 Lemma3.4和 L e m m a 3.5 Lemma 3.5 Lemma3.5似乎是矛盾的,因为粗略地说,当 O i O_i Oi和 S S S在同一连通分量中的概率很大时,给定S,加入 O i O_i Oi的边际影响会很小。为了正式的说明这一点,我们必须为连通分量的大小和连接性事件之间的相关性建立界限;这个界限在XYZ引理(引理3.6)中被定义。

这里作者给出了两个定义:

对于一个点 j ∈ E i j \in E_i j∈Ei,definition 1说 j j j对于 O i ∈ M ′ ′ O_i \in M'' Oi∈M′′是"exclusive":当 j j j在 M ′ ′ M'' M′′、 S S S的连通分量中,不在 H H H的连通分量中时, j j j被感染的概率依然小;
definition 2说 j j j对于 O i ∈ M ′ ′ O_i \in M'' Oi∈M′′是"good":definition 2想说的是, M ′ ′ M'' M′′和S都影响j的概率并不比 M ′ ′ M'' M′′影响 j j j的概率小多少。
最后,将XYZ引理应用于 M ′ M' M′和S,我们将证明, M ′ ′ M'' M′′中大部分的影响力都是由于 O i O_i Oi影响了一个"exclusive and good" j j j。
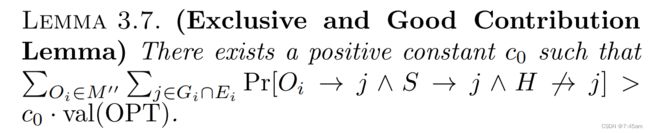
到目前为止,我们集齐了所有的武器,接下来可以证明theorem 3.1了。
这里证明的思路大概如下:先假设theorem 3.1不成立,即 v a l ( G R D ) ≤ ( 1 − 1 / e + c ) v a l ( O P T ) val(GRD)\leq (1-1/e+c)val(OPT) val(GRD)≤(1−1/e+c)val(OPT),那么由lemma 3.1,3.2和3.3可将OPT分解为 L , M ′ , M ′ ′ , H L,M',M'',H L,M′,M′′,H且满足lemma 3.5( ∣ M ′ ′ ∣ ≥ k / 3 a n d P r [ O i → S ] < 14 ϵ |M''| \geq k/3 and Pr[O_i \rightarrow S] < 14 \sqrt{\epsilon} ∣M′′∣≥k/3andPr[Oi→S]<14ϵ for all O i ∈ M ′ ′ O_i \in M'' Oi∈M′′)。通过随后的几个Lemma,作者证明了再这种情况下依然有 v a l ( S ) ≥ c 2 ⋅ 1 δ v a l ( O P T ) val(S) \geq c_2 \cdot \frac{1}{\delta}val(OPT) val(S)≥c2⋅δ1val(OPT)(这里S是GRD的前k个种子, δ = 14 ϵ \delta = 14\sqrt{\epsilon} δ=14ϵ),因此原结论成立。