手撕算法

标注*号的就是还没写完的题目

动态规划

1、最小路径和 ✔

最小路径和

思路:

1. n为行数，m为列数，设dp[][] 为n×m的矩阵， dp[i][j] 就是走到该位置的最小路径和
2. 确定边界：
   - 当 i = 0 ，j ≠ 0 时，只能从左边来，所以 grid[i][j] += grid[i][j-1];
   - 当 i ≠ 0 ，j = 0 时，只能从上边来，所以 grid[i][j] += grid[i-1][j];
   - 除去上面两种情况，其他都可以从上边或左边过来，这时候就要选择路径和更小的那个：
   grid[i][j] += Math.min( grid[i-1][j] , grid[i][j-1] );
3. 通过观察可以发现我们可以直接在原矩阵的基础上进行修改，而不需要占用额外的空间。

代码：

public int minPathSum(int[][] grid) {
        int n = grid.length,m = grid[0].length;
        
        for(int i = 0;i < n;i++){   //行
            for(int j = 0;j < m;j++){   //列
                if(i == 0 && j == 0) continue;
                else if(i == 0){
                    //第一行,只能从左边来
                    grid[i][j] += grid[i][j-1]; 
                }else if(j == 0){
                    //第一列,只能从上边来
                    grid[i][j] += grid[i-1][j]; 
                }else{
                    //非第一行第一列 需要判断哪边的值更小,就加哪边
                    grid[i][j] += Math.min(grid[i-1][j],grid[i][j-1]);
                }
            }
        }

        return grid[n-1][m-1];
    }

复杂度分析：

• 时间复杂度：O(n*m)，需要遍历整个矩阵一次
• 空间复杂度：O(1)

2、最长递增子序列 ✔

最长递增子序列

参考答案

这道题考虑使用动态规划：

我们定义dp[i]为当前index = i时数组的最长严格递增子序列长度。关键的问题在于我们怎么去计算dp数组的每个值。

状态转移公式

假设我们已经知道了 dp[0…4] 的所有结果，我们如何通过这些已知结果推出 dp[5] 呢？

很明显，nums[5] = 3，既然是递增子序列，我们只要找到前面那些结尾比 3 小的子序列，然后把 3 接到最后，就可以形成一个新的递增子序列，再将这个新的子序列长度加一

显然，可能形成很多种新的子序列，但是我们只选择最长的那一个，把最长子序列的长度作为 dp[5] 的值即可。

所以这道题我们需要做的有：

• 在刚开始时定义 dp[i] = 1，因为最短的序列就是单独一个数字
• 遍历数组的时候，比较 i（后） 与 j （前），如果 nums[i] > nums[j] 则 nums[i] 可以接上 nums[j] 成为一个更长的递增子序列。我们就可以让 dp[i] = Math.max(dp[i],dp[j]+1) <– 如果这一步能想明白，那么整道题就迎刃而解

代码：

public int lengthOfLIS(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n];
        Arrays.fill(dp, 1);   //将数组全部替换成1
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);   //最重要的公式，求出最长的递增子序列
                }
            }
        }
        int ans = 0;
        for (int i = 0; i < n; i++) {
            ans = Math.max(ans, dp[i]);   //遍历取出最大值
        }
        return ans;
    }

复杂度分析：

• 时间复杂度：O(n^2)，其中 n 为数组 nums 的长度。动态规划的状态数为 n，计算状态 dp[i] 时，需要 O(n) 的时间遍历 dp[0…i−1] 的所有状态，所以总时间复杂度为 O(n^2)
• 空间复杂度：O(n)，需要额外使用长度为 n 的 dp 数组。

3、三角形 ✔

三角形最小路径和

思路：

1. 使用动态规划，定义 dp[][] ，大小为n行m列，dp[i][j] 就是走到该位置的最小路径和
2. 确定边界： i为行数
   - 当 j = 0 时，只能从 j 来，所以 triangle.get(i).set ( j , triangle.get(i).get(j) + triangle.get(i-1).get(j));
   - 当 j = i 时，只能从 j-1 来，所以 triangle.get(i).set ( j , triangle.get(i).get(j) + triangle.get(i-1).get(j-1));
   - 除去上面两种情况，其他都可以从 j 或 j-1 过来，这时候就要选择路径和更小的那个：
   int min = Math.min ( triangle.get(i-1).get(j) , triangle.get(i-1).get(j-1) );
   triangle.get(i).set ( j , triangle.get(i).get(j) + min);
3. 当 i=n-1 时，即为最后一行，我们需要维护一个最小路径和ans

代码：

public int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
        if(n == 1) return triangle.get(0).get(0);   // 如果只有一行
        int ans = Integer.MAX_VALUE;   
        for(int i=1;i < n;i++){    //从第二行开始遍历
            for(int j = 0;j <= i;j++){
                // 列为0，即在左边，只能从j下来
                if(j == 0) triangle.get(i).set(j,triangle.get(i).get(j) + triangle.get(i-1).get(j));
                // 列为i，即在右边，只能从j-1下来
                else if(j == i) triangle.get(i).set(j,triangle.get(i).get(j) + triangle.get(i-1).get(j-1));
                // 列在中间，可以从j或j-1下来 需要判断
                else{
                    int min = Math.min(triangle.get(i-1).get(j),triangle.get(i-1).get(j-1));
                    triangle.get(i).set(j,triangle.get(i).get(j) + min);
                }
                if(i == n-1) ans = Math.min(ans,triangle.get(i).get(j));   //最后一行，维护最小答案
            }
        }    
        return ans;
    }

运行结果：

复杂度分析：

• 时间复杂度：O(n^2)，n为三角形行数，并且在更改原集合的情况下，我们频繁使用get和set方法，也会消耗一定的性能
• 空间复杂度：O(1)

看了题解之后的答案：

定义二维 dp 数组，自底向上的递推

状态定义：

dp[i][j] 表示从点 (i, j)到底边的最小路径和

状态转移方程（自底向上）：

dp[i][j] = min(dp[i+1][j],dp[i+1][j+1]) + triangle[i][j]

代码：

public int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
        // dp[i][j] 表示从点 (i, j) 到底边的最小路径和。
        int[][] dp = new int[n + 1][n + 1];
        // 从三角形的最后一行开始递推。
        for (int i = n - 1; i >= 0; i--) {
            for (int j = 0; j <= i; j++) {
                dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + triangle.get(i).get(j);
            }
        }
        return dp[0][0];
    }

复杂度分析：

• 时间复杂度：O(N^2)，N 为三角形的行数
• 空间复杂度：O(N^2)，N 为三角形的行数

空间优化：
在上述代码中，我们定义了一个 N 行 N 列 的 dp 数组
但是在实际递推中我们发现，计算 dp[i][j] 时，只用到了下一行的 dp[i + 1][j] 和 dp[i + 1][j + 1]
因此 dp 数组不需要定义 N 行，只要定义 1 行就足够：

public int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
        int[] dp = new int[n + 1];   //用于防止j+1越界
        for (int i = n - 1; i >= 0; i--) {
            for (int j = 0; j <= i; j++) {
                dp[j] = Math.min(dp[j], dp[j + 1]) + triangle.get(i).get(j);
            }
        }
        return dp[0];
    }

复杂度分析：

• 时间复杂度：O(N^2)，N 为三角形的行数
• 空间复杂度：O(N)，N 为三角形的行数

4、找零钱 ✔

零钱兑换

答案看的这个

思路:

1. dp[j] 代表的含义：就是amount在这个coins组合下最少用多少枚硬币

可以转化为完全背包问题 ： 填满容量为amount的背包最少需要多少硬币

2. 初始化dp的问题：后面要求的是最少的硬币，所以初始化不能对结果造成影响，而因为硬币的数量一定不会超过amount（面值最低为1），所以直接初始化dp数组的值为amount+1，特例 dp[0] = 0;

3. 最重要的转移方程： dp[j] = Math.min(dp[j], dp[j-coin] + 1)
   当前填满容量j最少需要的硬币 = min( 之前填满容量j最少需要的硬币, 填满容量 j - coin 需要的硬币 + 1个当前硬币）

4. 返回dp[amount]，如果dp[amount]的值为10001没有变过，说明找不到硬币组合，返回-1

代码：

public int coinChange(int[] coins, int amount) {
        int a = amount + 1;   
        int[] dp = new int[a];  //定义amount+1
        Arrays.fill(dp, a);  //因为硬币的数量一定不会超过amount
        dp[0] = 0;   //当amount == 0 时 返回0
        for(int coin : coins){
            for(int j = coin; j < a; j++){   //从每个硬币的面值开始遍历到amount
                    dp[j] = Math.min(dp[j], dp[j - coin] + 1);  
                   //这个转移方程就是dp[amount]在这个coins组合下最少用多少枚硬币
            }
        }
        return dp[amount] == a ? -1 : dp[amount];
    }

零钱兑换 II

–> 答案参考

思路：

1. dp[j] 代表 j 金额 在当前的 coins 组合下有多少种组合方式

也可转化为完全背包之组合问题——dp[j] 代表装满容量为j的背包有几种硬币组合

2. 列出转移方程：dp[j] = dp[j] + dp[j - coin]
   当前填满 j 容量的方法数 = 之前填满 j 容量的硬币组合数 + 填满 j - coin 容量的硬币组合数
   也就是当前硬币coin的加入，可以把 j - coin 容量的组合数加入进来
3. dp[0] = 1; 即金额为0时只有一种组合coins的方式（都不用）

代码：

public int change(int amount, int[] coins) {
        // dp[j] 代表 amount金额 在当前的 coins 组合下有多少种组合方式
        int[] dp = new int[amount+1];
        dp[0] = 1;
        for(int coin:coins){
            for(int j = coin;j < amount+1;j++){
                dp[j] = dp[j] + dp[j-coin];
            }
        }
        return dp[amount];
    }

5、最大字段和 ✔

最大子序和

这道题要我们找到一个具有最大和的连续子数组，可以转换为求以 i 结尾的连续子数组的最大和，考虑使用动态规划，列出转移方程：dp[i] = Math.max( dp[i-1]+nums[i] , nums[i] )，遍历数组输出dp[ ]最大值即可

代码：

public int maxSubArray(int[] nums) {
       //dp[i]表示下标j的连续子数组最大和
       int n = nums.length,ans = nums[0];
       int[] dp = new int[n];
       dp[0] = nums[0];
       for(int i = 0;i < n;i++){
            if(i != 0) dp[i] = Math.max(nums[i],dp[i-1]+nums[i]);
            ans = Math.max(dp[i],ans);
       } 
       return ans;
    }

但是通过观察我们可以发现，dp数组每次都只会使用dp[i]，我们可以考虑用一个数字pre代替dp数组，改进后的代码：

public int maxSubArray(int[] nums) {
        //简化 --> pre为前一个数的连续子数组最大和  
       int pre = 0,ans = nums[0];
       for(int num:nums){
           pre = Math.max(num,num+pre);
           ans = Math.max(ans,pre);
       }
       return ans;
    }

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

6、爬楼梯 ✔

爬楼梯

通过观察可知该题为斐波那契数列，根据数列特性可写出递归代码：

public int climbStairs(int n) {
        if(n == 1) return 1;
        if(n == 2) return 2;
        return climbStairs(n-1)+climbStairs(n-2);
    }

这样实现算法时空复杂度很高，并且有可能会导致栈溢出。

考虑使用正向循环（滚动数组）：

public int climbStairs(int n) {
        int a=0,b=0,sum=1;
        for(int i=1;i<=n;i++){
            a = b;
            b = sum;
            sum = a+b;
        }
        return sum;
    }

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

7、分割等和子集 ✔

分割等和子集

题解

思路：

1. 特例： 如果sum为奇数，那一定找不到符合要求的子集，返回False

2. dp[j]含义： 有没有和为j的子集，有为True，没有为False

3. 初始化dp数组： 长度为target + 1，用于存储子集的和从0到target是否可能取到的情况。
   比如和为0一定可以取到（也就是子集为空），那么dp[0] = True

4. 接下来开始遍历nums数组，对遍历到的数nums[i]有两种操作，一个是选择这个数，一个是不选择这个数。

   • 不选择这个数：dp不变
   • 选择这个数：dp中已为True的情况再加上nums[i]也为True。比如dp[0]已经为True，那么dp[0 + nums[i]]也是True

5. 在做出选择之前，我们先逆序遍历子集的和从nums[i]到target的所有情况，判断当前数加入后，dp数组中哪些和的情况可以从False变成True

   （为什么要逆序：是因为dp后面的和的情况是从前面的情况转移过来的，如果前面的情况因为当前nums[i]的加入变为了True，比如dp[0 + nums[i]]变成了True，那么因为一个数只能用一次，dp[0 + nums[i] + nums[i]]不可以从dp[0 + nums[i]]转移过来。如果非要正序遍历，必须要多一个数组用于存储之前的情况。而逆序遍历可以省掉这个数组）

   状态转移方程： dp[j] = dp[j] or dp[j - nums[i]]

   • 如果不选择当前数，那么和为j的情况保持不变，dp[j]仍然是dp[j]，原来是True就还是True，原来是False也还是False；
   • 如果选择当前数，那么如果j - nums[i]这种情况是True的话和为j的情况也会是True。比如和为0一定为True，只要 j - nums[i] == 0，那么dp[j]就变成了True
     
     

   dp[j]和dp[j-nums[i]]只要有一个为True，dp[j]就变成True，因此用or连接两者

6. 返回dp[target]

代码：

public boolean canPartition(int[] nums) {
        // 求出 sum 
        int sum = Arrays.stream(nums).sum();;
        // sum为奇数 说明不能分割为两个相等的子集
        if(sum % 2 == 1) return false;

        int target = sum >> 1;
        boolean[] dp = new boolean[target + 1];
        dp[0] = true;
        for(int num : nums){
            for(int j = target; j >= num; j--){
                dp[j] = dp[j] || dp[j - num];
            }
        }

        return dp[target];
    }

复杂度分析：

• 时间复杂度：O(n * target)
• 空间复杂度：O(target)

8、目标和 ✔

目标和

这道题用枚举递归也能做：

class Solution {

    int count = 0;
    public int findTargetSumWays(int[] nums, int S) {
        forSum(nums,S,0);
        return count;
    }

    public void forSum(int[] nums,int S,int i){
        if(S == 0 && i == nums.length){
            count ++;
            return;
        }

        if(i == nums.length) return;

        forSum(nums,S + nums[i],i + 1);
        forSum(nums,S - nums[i],i + 1);
    }
}

但是用递归时间复杂度是O(2^n)，其中n是数组nums的长度，时间复杂度为指数级别，效率比较差。

我们再看看dp：

大佬题解

思路：

1. 01背包问题是选或者不选，但本题是必须选，是选+还是选-。先将本问题转换为01背包问题。
   假设所有符号为+的元素和为x，符号为-的元素和的绝对值是y
   我们想要的 S = 正数和 - 负数和 = x - y
   而已知x与y的和是数组总和：sum = x + y
   可以求出 x = (S + sum) / 2 = target
   也就是我们要从nums数组里选出几个数，令其和为target
   于是就转化成了求容量为target的01背包问题 => 要装满容量为target的背包，有几种方案
2. 特例判断
   如果S大于sum，不可能实现，返回0
   如果x不是整数，也就是S + sum不是偶数，不可能实现，返回0
   比如： nums: [1, 1, 1, 1, 1], S: 4 => 无解
3. dp[j]代表的意义：填满容量为j的背包，有dp[j]种方法。因为填满容量为0的背包有且只有一种方法，所以dp[0] = 1
4. 状态转移：dp[j] = dp[j] + dp[j - num]，
   当前填满容量为j的包的方法数 = 之前填满容量为j的包的方法数 + 之前填满容量为j - num的包的方法数
   也就是当前数num的加入，可以把之前和为j - num的方法数加入进来。
5. 返回dp[target]

代码：

public int findTargetSumWays(int[] nums, int S) {
        // 求出sum
        int sum = 0;
        for(int num : nums){
            sum += num;
        }

        // 特例判断
        if(S > sum || (sum + S) % 2 == 1) return 0;

        int target = (sum + S) >> 1;
        int[] dp = new int[target + 1];
        dp[0] = 1;
        // 状态转移：dp[j] = dp[j] + dp[j - num]
        for(int num : nums){
            for(int j = target; j >= num; j--){
                dp[j] = dp[j] + dp[j - num];
            }
        }
        return dp[target];
    }

复杂度分析：

• 时间复杂度：O(n * target)
• 空间复杂度：O(target)

链表

1、链表逆序(反转链表) ✔

反转链表

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode pre = null,cur = head;
        ListNode temp = new ListNode(0);
        while(cur != null){
            temp = cur.next;     //暂存后继节点
            cur.next = pre;      //更改指向
            pre = cur;           //更新pre
            cur = temp;          //访问下一节点
        }
        return pre;
    }
}

复杂度分析：

• 时间复杂度：O(a+b),最差情况下（即 |a - b| = 1 , c=0 ），此时需遍历 a+b 个节点。
• 空间复杂度：O(1)

反转链表 II

思路:

• 使用一个count记录，把要反转的链表拿出来
• 对链表进行反转
• 将反转的链表接回原链表
  

结果看起来还行，但是自己思考的思路比较复杂，看了题解之后发现有更简洁的写法：

题解

思路：

1. 建一个虚拟头节点dummy，指向head节点
2. 建立hh指针，一直往右移动至left的前一位置
3. 使用a、b指针，将目标节点的next指针翻转
4. 让hh.next（也就是left节点）的next指针指向b
5. 让hh的next指针指向a
6. 返回dummy.next

代码：

public ListNode reverseBetween(ListNode head, int l, int r) {
        ListNode dummy = new ListNode(0);
        dummy.next = head;
        r -= l;    // 调整r指针 变成要被反转的链表的步数
        ListNode hh = dummy;
        
        while (l-- > 1) hh = hh.next;     
        // ↑ 使hh指针在要被反转的前一个位置上,此时a在翻转链表的第一个元素,b在第二个
        ListNode a = hh.next, b = a.next;
        
        while (r-- > 0) {   // 每走一步 r--
            ListNode tmp = b.next;  
            b.next = a;
            a = b;
            b = tmp;
        }
        
        hh.next.next = b;
        hh.next = a;
        return dummy.next;
    }
    

2、链表求交点 ✔

相交链表

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        //双指针  在A的尾部衔接上B  两个指针一起走  
        //最后如果相同就返回A  不相同走到最后 A B均为null
        ListNode A = headA, B = headB;
        while (A != B) {
            A = A != null ? A.next : headB;
            B = B != null ? B.next : headA;
        }
        return A;

        //另外一个版本的双指针  如果A比B长 就先让A走(A-B)步 再双指针遍历 
        //如果有相同点返回A 没有相同点返回null   比较麻烦
    }

复杂度分析：

• 时间复杂度：O(N)
• 空间复杂度：O(1)

3、链表求环(环形链表) ✔

环形链表

同样使用双指针求解,快慢指针一起遍历链表,如果两指针相遇则说明存在环,反之则不存在

public boolean hasCycle(ListNode head) {
        if(head == null) return false;
        ListNode fast = head.next;
        ListNode slow = head;
        while(slow != fast){
            if (fast == null || fast.next == null) {
                return false;
            }
            fast = fast.next.next;  //快指针一次走两步
            slow = slow.next;
        }
        return slow == null ? false:true;
    }

复杂度分析：

• 时间复杂度：O(N)，其中 N 是链表中的节点数。
• 空间复杂度：O(1),我们只使用了两个指针的额外空间。

环形链表II

4、复杂链表的复制 ✔

复杂链表的复制

思路:

1. 使用HashMap 复制各节点，并建立 “原节点 -> 新节点” 的 Map 映射
   即 map.put(cur, new Node(cur.val));
2. 构建新链表的 next 和 random 指向
3. 最后直接返回新链表的头节点即可

代码:

public Node copyRandomList(Node head) {
        if(head == null) return null;
        Node cur = head;
        Map<Node, Node> map = new HashMap<>();
        // 复制各节点，并建立 “原节点 -> 新节点” 的 Map 映射
        while(cur != null) {
            map.put(cur, new Node(cur.val));
            cur = cur.next;
        }
        cur = head;
        // 构建新链表的 next 和 random 指向
        while(cur != null) {
            map.get(cur).next = map.get(cur.next);
            map.get(cur).random = map.get(cur.random);
            cur = cur.next;
        }
        // 返回新链表的头节点
        return map.get(head);
    }

复杂度分析:

• 时间复杂度：O(N)，两轮遍历链表，使用 O(N)时间
• 空间复杂度：O(N)，哈希表使用了线性大小的额外空间

5、两个排序链表的归并 ✔

合并两个有序链表

public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        //递归调用解法
        if(l1 == null || l2 == null) return l1 == null ? l2:l1;
        else if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        }
        else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }

6、k个排序链表的归并 ✔

合并k个升序链表

偷懒暴力解决法:

能想到的最朴素的方法就是循环,用一个ans作为主链,k个链表作为副链 循环两两合并:

	public ListNode mergeKLists(ListNode[] lists) {
        //最朴素的方法
        ListNode ans = null;
        for (int i = 0; i < lists.length; ++i) {
            ans = mergeTwoLists(ans, lists[i]);
        }
        return ans;
    }
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        //递归调用解法
        if(l1 == null || l2 == null) return l1 == null ? l2:l1;
        else if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        }
        else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }

复杂度分析:

• 空间复杂度: O(1)
• 时间复杂度: O(n*k^2)

结果:

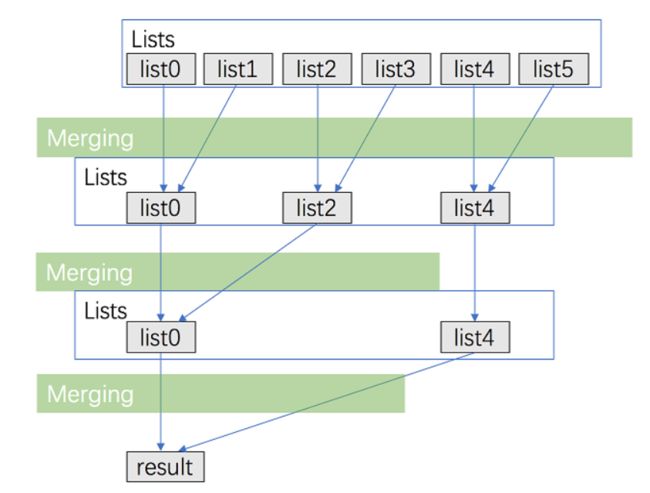
分治法:

其实我第一个想到的是分治法,但是具体实现并不简单,看了题解之后的答案:

分治法图解 :

代码:

public ListNode mergeKLists(ListNode[] lists) {
        return merge(lists, 0, lists.length - 1);
    }

    public ListNode merge(ListNode[] lists, int l, int r) {
        if (l == r) {
            return lists[l];
        }
        if (l > r) {
            return null;
        }
        int mid = (l + r) >> 1;
        // ↓ 最重要的是这一步,方法递归方法
        return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
    }

    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        //递归调用解法
        if(l1 == null || l2 == null) return l1 == null ? l2:l1;
        else if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        }
        else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }

结果:

复杂度分析:

二分查找

1、旋转数组的查找 ✔

搜索旋转排序数组

排序数组的旋转规律有迹可循，我们可以通过判断左边半个数组的端点 nums[left] 与 nums[mid] 的关系可以得出左边是否是有序的，如果左半数组有序则右半数组无序，反之亦然

通过思考可以写出以下代码：

public int search(int[] nums, int target) {
        //特殊情况判断
        if(nums.length == 0) return -1;
        if(nums.length == 1) return nums[0]==target ? 0:-1;

        int l = 0,r = nums.length-1;   //定义两个端点
        while(l <= r){
            int mid = l+(r-l)/2;
            if(nums[mid] == target) return mid;
            //判断中点左边是否有序,如果有序则右边无序,如果无序则右边有序
            // 1.左边有序
            if(nums[l]<=nums[mid]){
                if(target>=nums[l] && target<nums[mid]){
                    // target在左
                    r = mid-1;
                }else{
                    // target在右
                    l = mid+1;
                }
            }else{
            // 2.右边有序
                if(target>nums[mid] && target<=nums[r]){
                    // target在右
                    l = mid+1;
                }else{
                    // target在左
                    r = mid-1;
                }
            }
        }
        return -1;
    }

搜索旋转排序数组II
与搜索旋转排序数组相比，本题中的 nums 可能包含重复元素，所以我们需要考虑的情况多了一种：

1. [10111] 和 [11101] 这种。此种情况下 nums[left] == nums[mid]，分不清到底是前面有序还是后面有序，此时 left++ 即可。相当于去掉一个重复的干扰项
2. 依旧判断中点左边是否有序，如果有序则右边无序，如果无序则右边有序

代码：

public boolean search(int[] nums, int target) {
        //特殊情况判断
        if(nums.length == 0) return false;
        if(nums.length == 1) return nums[0]==target ? true:false;

        //定义指针
        int l = 0 , r = nums.length-1;
        while(l <= r){
            int mid = l + ((r-l)>>1);   //l+(r-l)是为了防止溢出 使用>>1是因为位运算速度更快
            if(nums[mid] == target) return true;
            if(nums[l] == nums[mid] && l<nums.length-1){
                l++;                         //将l指针移到没有重复元素的位置
                continue;   
            }
            //判断中点左边是否有序,如果有序则右边无序,如果无序则右边有序
            // 1.左边有序
            if(nums[l]<=nums[mid]){
                if(target>=nums[l] && target<nums[mid]){
                    // target在左
                    r = mid-1;
                }else{
                    // target在右
                    l = mid+1;
                }
            }else{
            // 2.右边有序
                if(target>nums[mid] && target<=nums[r]){
                    // target在右
                    l = mid+1;
                }else{
                    // target在左
                    r = mid-1;
                }
            }
        }
        return false;
    }

搜索旋转数组

这题与搜索旋转排序数组的差别在于数组不止被旋转了一次，并且还会出现重复元素
但实际上旋转多次与旋转一次对于这道题没有什么区别，所以只需要解决这道题重复元素输出索引值最小的问题就可以了

综上，我们需要考虑的情况：

1. 当nums[mid] == target 时，我们不能确定mid前面是否有重复元素，所以我们将右指针right=mid，再进行循环去判断即可
2. [10111] 和 [11101] 这种。此种情况下 nums[left] == nums[mid]，分不清到底是前面有序还是后面有序，此时 left++ 即可。相当于去掉一个重复的干扰项
3. 依旧判断中点左边是否有序，如果有序则右边无序，如果无序则右边有序

代码：

public int search(int[] nums, int target) {
        //特殊情况判断
        if(nums.length == 0) return -1;
        if(nums.length == 1) return nums[0] == target ? 0:-1;

        //定义左右指针
        int l=0,r=nums.length-1;
        while(l <= r){
            int mid = l + ((r-l)>>1);
            if(nums[l] == target) return l;
            //当mid==target时要判断它前面有没有重复元素  直接让r=mid继续循环
            if(nums[mid] == target){
                r = mid;
                continue;
            }
            // 排除重复干扰
            if(nums[l] == nums[mid]){
                l++;
                continue;
            }

            //左边有序的情况
            if(nums[l] <= nums[mid]){
                //落在左边
                if(target >= nums[l] && target <= nums[mid]){
                    r = mid-1;
                }else{ //落在右边
                    l = mid+1;
                }
            }else{   //右边有序的情况
                if(target >= nums[mid] && target <= nums[l]){
                    //落在右边
                    l = mid+1; 
                }else{
                    //落在左边
                    r = mid-1;
                }
            }
        }
        return -1;
    }

寻找旋转排序数组中的最小值

这题不再给定target，而是要求我们求出nums中的最小值，我们依旧可以判断出旋转数组是在中点左边有序或在中点右边有序，所以我们只需要找出最小值即可

综上，我们要做的有：

1. 判断数组中点左边或右边有序
2. 如果是左边有序，判断端点 ：
   nums[left] < nums[right] 说明数组完全升序，直接输出 nums[left]
   nums[left] >= nums[right] 说明有更小的数存在于右半数组，将 l = mid+1 继续下次循环
3. 如果右边有序：
   nums[mid] < nums[mid-1] 直接输出nums[mid]
   nums[mid] >= nums[mid-1] 说明有更小的数存在于右半数组，将 r = mid-1 继续下次循环

代码：

    public int findMin(int[] nums) {
        //定义左右指针
        int l=0,r=nums.length-1;
        while(l < r){
            int mid = l+((r-l) >> 1);
            //左边有序
            if(nums[l] <= nums[mid]){
                if(nums[l] < nums[r]) return nums[l];
                else l = mid+1;
            }else{
                //右边有序
                if(nums[mid] < nums[mid-1]) return nums[mid];
                else r = mid-1;
            }
        }
        return nums[l];
    }

困难题: 寻找旋转排序数组中的最小值 II

这道题也是要求我们求出数组中的最小值，但是其中可能会存在重复元素

我们需要考虑的情况：

1. 当nums[left] == nums[mid] 且 left != mid 时，证明左边数组有重复元素，排除重复元素干扰后 再进行循环即可
2. 如果是左边有序，判断端点 ：
   nums[left] < nums[right] 说明数组完全升序，直接输出 nums[left]
   nums[left] >= nums[right] 说明有更小的数存在于右半数组，将 l = mid+1 继续下次循环
3. 如果右边有序：
   nums[mid] < nums[mid-1] 直接输出nums[mid]
   nums[mid] >= nums[mid-1] 说明有更小的数存在于右半数组，将 r = mid-1 继续下次循环

代码：

public int findMin(int[] nums) {
        //定义左右指针
        int l=0,r=nums.length-1;
        while(l < r){
            int mid = l+((r-l) >> 1);
            //排除重复项干扰  l!=mid是为了不要误伤当length==2的情况
            if(l != mid && nums[l] == nums[mid]){
                l++;
                continue;
            }
            //左边有序
            if(nums[l] <= nums[mid]){
                if(nums[l] < nums[r]) return nums[l];
                else l = mid+1;
            }else{
                //右边有序
                if(nums[mid] < nums[mid-1]) return nums[mid];
                else r = mid-1;
            }
        }
        return nums[l];
    }

2、区间查找 ✔

在排序数组中查找元素的第一个和最后一个位置

思路:

• 使用二分查找，分别遍历一次nums，找出第一个位置和最后一个位置

代码：

public class Solution {
    public int[] searchRange(int[] nums, int target) {
        if (nums.length == 0) return new int[]{-1, -1};

        int first = findFirstPosition(nums, target);
        if (first == -1) return new int[]{-1, -1};

        int last = findLastPosition(nums, target);
        return new int[]{first, last};
    }

    private int findFirstPosition(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            // 小于一定不是解
            if (nums[mid] < target) {
                // 下一轮搜索区间是 [mid + 1, right]
                left = mid + 1;
            } else if (nums[mid] == target) {
                // 因为在找第一个位置，所以下一轮搜索区间是 [left, mid]
                right = mid;
            } else {
                // nums[mid] > target，下一轮搜索区间是 [left, mid - 1]
                right = mid - 1;
            }
        }

        if (nums[left] == target) return left;
        return -1;
    }

    private int findLastPosition(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        while (left < right) {
            int mid = left + (right - left + 1) / 2;
            if (nums[mid] > target) {
                // 下一轮搜索区间是 [left, mid - 1]
                right = mid - 1;
            } else if (nums[mid] == target){
                // 因为在找最后的位置，所以下一轮搜索区间是 [mid, right]
                left = mid;
            } else {
                // nums[mid] < target，下一轮搜索区间是 [mid + 1, right]
                left = mid + 1;
            }
        }
        return left;
    }
}

复杂度分析：

• 时间复杂度：O(log N)，这里 N 是数组的长度，两个子问题都是二分查找，因此时间复杂度为对数级别
• 空间复杂度：O(1)，只使用了常数个数的辅助变量、指针

3、逆序数 *

困难题： 数组中的逆序对

4、二叉查找树的编码与解码 ✔

序列化和反序列化二叉搜索树

代码:

public class Codec {

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        //边界判断，如果为空就返回一个字符串"#"
        if (root == null)
            return "#";
        return root.val + "," + serialize(root.left) + "," + serialize(root.right);
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        //把字符串data以逗号","拆分，拆分之后存储到队列中
        Queue<String> queue = new LinkedList<>(Arrays.asList(data.split(",")));
        return helper(queue);
    }

    private TreeNode helper(Queue<String> queue) {
        //出队
        String sVal = queue.poll();
        //如果是"#"表示空节点
        if ("#".equals(sVal))
            return null;
        //否则创建当前节点
        TreeNode root = new TreeNode(Integer.valueOf(sVal));
        //分别创建左子树和右子树
        root.left = helper(queue);
        root.right = helper(queue);
        return root;
    }

}

5、插入位置 ✔

搜索插入位置

思路: 二分查找

public int searchInsert(int[] nums, int target) {
        int l = 0,r = nums.length-1;
        while(l <= r) {
            int mid = l + ((r - l) >> 1);
            if (nums[mid] == target) return mid;
            else if (nums[mid] > target) r = mid - 1;
            else l = mid + 1;
        }
        return l;
    }

复杂度分析:

• 时间复杂度:O(logN)
• 空间复杂度:O(1)

栈 队列 堆

1、使用队列实现栈 ✔

用队列实现栈

思路：

• 使用基本队列， 每当push新元素，如果队列中有元素，则出队后再重新入队，达到后入先出的效果

代码：

class MyStack {
    Queue<Integer> queue;

    /** Initialize your data structure here. */
    public MyStack() {
        queue = new LinkedList<Integer>();
    }
    
    /** Push element x onto stack. */
    public void push(int x) {
        int n = queue.size();
        queue.offer(x);
        for (int i = 0; i < n; i++) {
            queue.offer(queue.poll());
        }
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        return queue.poll();
    }
    
    /** Get the top element. */
    public int top() {
        return queue.peek();
    }
    
    /** Returns whether the stack is empty. */
    public boolean empty() {
        return queue.isEmpty();
    }
}

2、使用栈实现队列 ✔

用栈实现队列

思路：

• 定义两个栈来模拟队列

代码：

class MyQueue {
    Stack<Integer> stack1;
    Stack<Integer> stack2;
    /** Initialize your data structure here. */
    public MyQueue() {
        stack1 = new Stack<Integer>();
        stack2 = new Stack<Integer>();
    }
    
    /** Push element x to the back of queue. */
    public void push(int x) {
    	// 先倒一次
        while(!stack1.empty()){
            stack2.push(stack1.pop()); 
        }
        stack1.push(x);  // 在空的stack1压入元素
        // 再倒一次  实现先进先出
        while(!stack2.empty()){
            stack1.push(stack2.pop());
        }
    }
    
    /** Removes the element from in front of queue and returns that element. */
    public int pop() {
        return stack1.pop();
    }
    
    /** Get the front element. */
    public int peek() {
        return stack1.peek();
    }
    
    /** Returns whether the queue is empty. */
    public boolean empty() {
        return stack1.empty();
    }
}

3、包含min函数的栈 ✔

包含min函数的栈

思路：

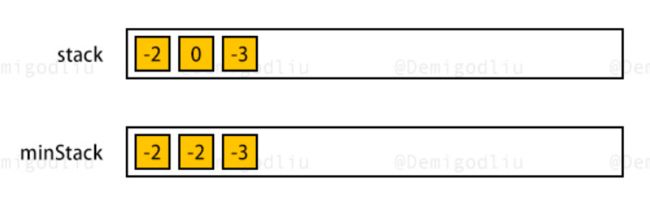
• 使用辅助栈，当入栈元素比辅助栈栈顶小或辅助栈为空时将元素压入辅助栈
• 这里有一个需要注意的地方：当入栈元素比辅助栈栈顶元素大时，我们选择不压入该元素，但是应该再次压入当前辅助栈栈顶元素，防止辅助栈提前被取空
  

代码：

class MinStack {

    Stack<Integer> stack;
    Stack<Integer> min;
    /** initialize your data structure here. */
    public MinStack() {
        stack = new Stack<Integer>();
        min = new Stack<Integer>();
    }
    
    public void push(int x) {
        stack.push(x);
        // if(min.size() == 0 || x < min.peek()) min.push(x);
        // else min.push(min.peek());
        min.push(Math.min(min.peek(), x));
    }
    
    public void pop() {
        min.pop();
        stack.pop();
    }
    
    public int top() {
        return stack.peek();
    }
    
    public int min() {
        return min.peek();
    }
}

4、简单的计算器 *

困难题:基本计算器

5、数组中第k大的数 ✔

数组中的第K个最大元素

思路:

• 主要是考手写快排，要特别注意边界条件
• 下面的代码是一个快排模板，也可以再精简

代码：

class Solution {
    public int findKthLargest(int[] nums, int k) {
        quickSort(nums,0,nums.length-1);
        return nums[nums.length - k];
    }

    /**
     快排
     */
    public void quickSort(int[] nums,int leftBound,int rightBound) {
        if(leftBound >= rightBound) return;
        int mid = partition(nums,leftBound,rightBound);
        // 递归过程
        quickSort(nums,leftBound,mid-1);
        quickSort(nums,mid+1,rightBound);
    }

    // 分区排序 
    public int partition(int[] nums,int leftBound,int rightBound){
        int pivot = nums[rightBound];
        int l = leftBound,r = rightBound -1;
        while(l < r){
            while(l <= r && nums[l] <= pivot) l++;
            while(l <= r && nums[r] > pivot) r--;

            if(l < r) swap(nums,l,r);
        }
        // 把轴放到该放的位置
        if(pivot < nums[l]) swap(nums,l,rightBound);

        return l;
    }

    public void swap(int[] n,int i,int j){
        int temp = n[i];
        n[i] = n[j];
        n[j] = temp;
    }
}

复杂度分析：

• 时间复杂度：最好情况O（N*logN），最差情况（即数组完全顺序或完全逆序，并且取的pivot并不随机导致）为O（N^2）
• 空间复杂度：如果考虑递归占用一定的临时空间则为O（logN），如果不考虑则为O（1）

6、寻找中位数 ✔

困难题: 寻找两个正序数组的中位数

思路：

简化版本的归并排序:

public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int i=0;//定义数组nums1的指针
        int j=0;//定义数组nums2的指针
        int k=0;//定义数组nums3的指针
        int [] nums3 = new int[nums1.length+nums2.length];
        while(i < nums1.length && j < nums2.length){
            if(nums1[i] <= nums2[j]){
                nums3[k] = nums1[i];
                k++;
                i++;
            }else if(nums1[i] > nums2[j]){
                nums3[k] = nums2[j];
                k++;
                j++;
            }
        }
        while(i < nums1.length) nums3[k++] = nums1[i++];//剩余nums1处理
        while(j < nums2.length) nums3[k++] = nums2[j++];//剩余nums2处理

        if(nums3.length % 2 == 0) return (double)(nums3[nums3.length / 2] + nums3[(nums3.length / 2) - 1]) / 2;
        else return (double)nums3[nums3.length / 2];
    }

字符串

1、最长回文串 ✔

最长回文串

这道题并不需要我们输出最长回文串，只需要输出最长回文串的长度，所以可以考虑使用HashMap建立映射，看了题解后发现可以用int数组来存储各个字母出现的次数，所以我们使用了一个长度为 128 的数组，存储每个字符出现的次数，这是因为字符的 ASCII 值的范围为 [0, 128)。

我们需要考虑的有：

1. 遍历 s.toCharArray() ，存储每个字母出现的次数
2. 遍历数组，记录奇数出现的次数count
3. 当 count == 0 时直接返回结果，当 count != 0 时说明有奇数，用s.length - count 后再+1（可以让一个奇数存在在回文串的中间）

代码如下：

public int longestPalindrome(String s) {
        int[] arr = new int[128];  //我们使用了一个长度为 128 的数组，存储每个字符出现的次数，
                                   // 这是因为字符的 ASCII 值的范围为 [0, 128)
        for(char c : s.toCharArray()) {
            arr[c]++;              //存储每个字母出现的次数
        }
        int count = 0;
        for (int i : arr) {
            count += (i % 2);       //存储奇数出现的个数
        }
        return count == 0 ? s.length() : (s.length() - count + 1);
    }

2、重复的DNA序列 ✔

重复的DNA序列

这道题暴力循环肯定超时，可以考虑使用set，每遍历一组就将其放入，在加入之前判断 HashSet 中是否存在，如果存在就说明和之前的发生重复，就把它加到结果中。从而我们可以减少一层循环。

代码：

class Solution {
    public List<String> findRepeatedDnaSequences(String s) {
        int len = s.length();
        Set<String> res = new HashSet<>();
        Set<String> set = new HashSet<>();
        for (int i = 0; i <= len - 10; i++) {
        String key = s.substring(i, i + 10);
         //之前是否存在
        if (set.contains(key)) {
            res.add(key);
        } else {
            set.add(key);
        }

        }   
        return new ArrayList<>(res);
    }   
}

3、最小窗口子串 *

最小覆盖子串

本题思路：

4、无重复字符的最长子串 ✔

无重复字符的最长字串

本题思路:

1. 使用滑动窗口遍历整个字符串
2. 没有发现重复元素时，固定左指针，将右指针的字符添加到Hashset，并让右指针+1
3. 每次当右指针发现重复元素时，固定右指针，将左指针的字符从Hashset中remove，再让左指针+1
4. 每次发现重复字符时，输出 res = Math.max(res,r-l) ，但此处需要进行边界处理，当 r = s.length() -1 并且该字符没有重复时，直接 return res = Math.max(res,r-l+1);

代码：

public int lengthOfLongestSubstring(String s) {
        if(s.length() == 0) return 0;
        int l = 0,r = 0,res = 0;
        Set<Character> map = new HashSet<>();
        while(r < s.length()){
            //判断-->右指针右移-->左指针右移
            if(!map.contains(s.charAt(r))) {
                if(r == s.length()-1){
                    return res = Math.max(res,r-l+1);
                }
                map.add(s.charAt(r++));     //右指针向右移动，先存入当前右指针的字符
            }else{
                res = Math.max(res,r-l);    
                map.remove(s.charAt(l++));    //左指针向右移动,移除当前左指针的字符
            }
        }
        return res;
    }

复杂度分析：

• 时间复杂度：O(N)，其中 N 是字符串的长度。右指针会遍历整个字符串一次。
• 空间复杂度：O(∣Σ∣)，其中 Σ 表示字符集（即字符串中可以出现的字符），∣Σ∣ 表示字符集的大小。在本题中没有明确说明字符集，因此可以默认为所有 ASCII 码在 [0,128) 内的字符，即 ∣Σ∣=128。我们需要用到哈希集合来存储出现过的字符，而字符最多有 ∣Σ∣ 个，因此空间复杂度为 O(∣Σ∣)。

5、同字符词语分组 ✔

字母异位词分组

题解

思路:

• 先将字符串转换为char数组
• 使用数组的sort方法将字母进行排序
• 因为排序后的顺序相同，我们可以将排序后的字符串作为map的key，如果key相同那最后存入的位置一定相同

代码：

public List<List<String>> groupAnagrams(String[] strs) {
        // 由于互为字母异位词的两个字符串包含的字母相同，
        // 因此对两个字符串分别进行排序之后得到的字符串一定是相同的，
        // 故可以将排序之后的字符串作为哈希表的键。 
        Map<String, List<String>> map = new HashMap<String, List<String>>();
        for (String str : strs) {
            char[] array = str.toCharArray();
            Arrays.sort(array);
            String key = new String(array);
            List<String> list = map.getOrDefault(key, new ArrayList<String>());
            list.add(str);
            map.put(key, list);
        }
        return new ArrayList<List<String>>(map.values());
    }

贪心算法

1、分糖果 ✔

分糖果

这道题需要把最多种类的糖果分给妹妹，弟弟可以忽略，其实就是相当于从数组中取出1/2最多种类的糖果，糖果种类可以分成以下情况：

1. 糖果种类 count >= n/2，这种情况妹妹可以得到最多的 n/2 种糖果
2. 糖果种类 count < n/2，这种情况妹妹只能得到 count 种糖果

方法一：
我们可以考虑通过 Arrays.sort() 来对数组进行排序，之后遍历数组比较相邻的两个数组，且当 count >= n/2 时我们可以提前中止遍历，输出 count

代码：

public int distributeCandies(int[] candies) {
        //排序法
        Arrays.sort(candies);
        int count = 1;
        for (int i = 1; i < candies.length && count < candies.length / 2; i++)
            if (candies[i] > candies[i - 1])
                count++;
        return count;
    }

复杂度分析:

• 时间复杂度：O(n log n)，其中排序方法需要O(log n)时间
• 空间复杂度：O(1)

方法二：
找到唯一元素数量的另一种方法是遍历给定 candies 数组的所有元素，并继续将元素放入集合中。通过集合的属性，它将只包含唯一的元素。最后，我们可以计算集合中元素的数量，例如 count。要返回的值将再次由 min(count,n/2) 给出，如前面的方法所述。其中 n 表示 candies 数组的大小。

代码：

//set集合
        HashSet < Integer > set = new HashSet < > ();
        for (int candy: candies) {
            set.add(candy);
        }
        return Math.min(set.size(), candies.length / 2);

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)，最坏情况下，set的大小为n

分糖果 II

这道题是那candies个糖果分给 n个人，如分给四个人：第一轮分 [1,2,3,4]，第二轮 [5,6,7,8] ，以此类推。

考虑直接循环遍历数组，每一轮发给当前小朋友 i 的糖果数为 i+1+(round-1)×n ，在每一轮结束后round+1

代码：

public int[] distributeCandies(int candies, int n) {
        int round = 1;        //定义轮数
        int[] res = new int[n];
        while(candies>0){
            for(int i=0;i<n;i++){
                int num = i+1+(round-1)*n;
                if(candies >= num){
                    candies -= num;
                    res[i] += num;
                }else{
                    res[i] += candies;
                    return res;
                }
            }
            round++;
        }
        return res;
    }

复杂度分析：

• 时间复杂度：O(s)，s为发完糖果要循环数组的步数
• 空间复杂度：O(1)

2、跳跃游戏1 2 ✔

跳跃游戏 I
给定一个非负整数数组nums，数组中的每个元素代表你在该位置可以跳跃的最大长度，判断是否能够到达最后一个下标。

方法一：扫描遍历

这道题如果数组都不为0，则我们一定可以到达最后一个下标，如果存在0，那么需要存在最大长度能够越过这个0的数字，否则无法到达。

综上，我们需要注意的有：

1. 除最后一个元素外，如果所有元素都不为0，那么一定可以走到最后
2. 从后往前扫描数组，当遇到0时，扫描当前下标 j 前的元素，判断是否存在 i 使得 nums[i] >= j-i+1 （越过j这个0元素）

代码：

public boolean canJump(int[] nums) {
        if(nums.length == 1) return true;
        int j = nums.length-1;
        while(j >= 0){
            if(nums[j] == 0 && j != nums.length-1){
                int i=j;
                while(i >= 0){
                    if(nums[i] >= j-i+1) break;
                    i--;
                }
                if(i < 0) return false;
            }
            j--;
        }
        return true;
    }

方法二：贪心算法

如果这道题能够想到当一个位置可达时，该位置左边的所有位置都可达，就不难想到我们可以依次遍历数组中的每一个位置，并实时维护 最远可以到达的位置 k 。对于当前遍历到的位置 x，如果它在 最远可以到达的位置 的范围内，那么我们就可以从起点通过若干次跳跃到达该位置，因此我们可以用 x+nums[x] 更新 k

public boolean canJump(int[] nums) {
        int k = 0,n = nums.length;    //k为最大可达距离
        for (int i = 0; i < n; ++i) {
            if (i <= k) {  //如果当前位置i可达
                k = Math.max(k, i + nums[i]);   //判断 更新k i为当前位置,nums[i]为当前位置能走的步数,
                                                // i+nums[i]就是当前位置可达的最大距离
                if (k >= n - 1)  return true;   //如果k已经能够达到最后一个下标,提前返回,减少循环
            }
        }
        return false;
    }

跳跃游戏 II

给定一个非0数组，即一定可以到达数组最后一个位置，现在要求我们求出跳到最后的位置需要的最少次数，使用贪心算法的核心思路：反向搜索最远能抵达position的位置，position从最后一个位置开始，即可求出需要的最少步数

代码：

class Solution {
    public int jump(int[] nums) {
        int position = nums.length - 1;
        int steps = 0;
        while (position > 0) {
            for (int i = 0; i < position; i++) {
                // 搜索最远能跳到position的位置
                if (i + nums[i] >= position) {
                    position = i;
                    steps++;
                    break;
                }
            }
        }
        return steps;
    }
}

复杂度分析：

• 时间复杂度：O（N）
• 空间复杂度：O（1）

3、剪绳子 ✔

剪绳子

这道题要求我们将长度为 n 的绳子剪为 m 段(m > 1)，看了题解之后的答案：

我们可以使用贪心算法，核心思路是：尽可能把绳子分为长度为3的小段，这样乘积最大

为什么长度为3的小段乘积最大：看这里

明确了任务之后，我们要做的步骤如下：

1. 考虑特殊情况：当 n == 2 时 直接返回1，当n == 3 时直接返回2，合起来为当 n < 4 时返回 n - 1，当 n == 4 时返回4
2. n > 4 时，每次循环都将 n - 3 ，再将 res × 3 ，返回结果 res × 剩下的不足3的 n

代码：

    public int cuttingRope(int n) {
        if(n < 4) return n - 1;
        int res = 1;
        while(n > 4){
            res *= 3;
            n -= 3;
        }
        return res * n;
    }

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

4、最优加油方法 *

最低加油次数

5、移除k个数字 ✔

移除k个数字

题解

思路：

• 使用单调栈存储每个取出的数字，当这个 取出的数字比栈顶的数字大 并且 要删除的数字k不为0 时，替换栈顶的元素

代码：

class Solution {
    public String removeKdigits(String num, int k) {
        int n = num.length();
        if(n == k) return "0";

        // 使用单调栈存储
        Deque<Character> stack = new LinkedList<>();

        char[] c = num.toCharArray();
        for(int i = 0;i < n;i++){
            while(!stack.isEmpty() && c[i] < stack.peekLast() && k > 0){
                stack.removeLast();
                k--;
            }
            stack.addLast(c[i]);
        }

        StringBuilder res = new StringBuilder();
        boolean firstZero = true;
        // 此处 !=k 是为了防止当数字为单调递增或部分单调递增的情况时，
        // k不会减到0，此时要裁剪字符串
        while(stack.size() != k){  
            if(firstZero && stack.peekFirst() == '0'){
                stack.removeFirst();
                continue;
            }
            firstZero = false;   // 不管首位是不是0 第一次循环以后设置为false
            res.append(stack.removeFirst());
        }


        return res.length() == 0 ? "0" : res.toString();
    }
}

复杂度分析：

• 时间复杂度：O(n)，其中 nn 为字符串的长度。尽管存在嵌套循环，但内部循环最多运行 k 次。由于 0 < k ≤ n，主循环的时间复杂度被限制在 2n 以内。对于主循环之外的逻辑，它们的时间复杂度是 O(n)，因此总时间复杂度为 O(n)。
• 空间复杂度：O(n)，栈存储数字需要线性的空间。

二叉树

1、二叉树转链表 ✔

二叉树转链表

递归分治解法:

public void flatten(TreeNode root) {
        //思路:使用递归  分治法
        if(root == null) return;
        if(root.right != null && root.left != null){
            TreeNode temp = root.left;  //定义temp存储root.left
            							//用于待会遍历到最后 接上root.right
            flatten(root.right);
            flatten(root.left);
            while(temp.right != null) temp = temp.right;  //开始遍历
            temp.right = root.right;   //接上
            root.right = root.left;    //全部接在右节点
        }else if(root.right != null){
            flatten(root.right);
        }else{
            flatten(root.left);
            root.right = root.left;
        }
        root.left = null;
    }

复杂度分析:

• 空间复杂度: O(H) H为树的高度，空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 (logN)。
• 时间复杂度: O(N)

2、路径之和 ✔

路径总和I

这个题比较简单,很容易就想到了递归解法:

public boolean hasPathSum(TreeNode root, int targetSum) {
        //思路:递归
        if(root == null) return false;
        if(root.left == null && root.right == null) return root.val==targetSum;
        return hasPathSum(root.left,targetSum-root.val)||hasPathSum(root.right,targetSum-root.val);
    }

复杂度分析:

• 时间复杂度: O(N) ，其中 N 是树的节点数。对每个节点访问一次。
• 空间复杂度: O(H) H为树的高度，空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 (logN)。

路径总和II

比较难的是这道题 要求我们将所有符合的路径存在数组中返回，考虑使用回溯法(深度优先):

代码:

class Solution {

    List<List<Integer>> res = new ArrayList<>();
    Deque<Integer> path = new ArrayDeque<>();
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        if(root == null) return res;
        path.add(root.val);
        backtracking(root,targetSum,root.val);
        return res;
    }

    // 因为有负数,所以得将sum参数加上
    public void backtracking(TreeNode root,int targetSum,int sum){
        if(root == null) return;

        // 有答案时还要判断是否是叶子节点
        if(sum == targetSum && root.left == null && root.right == null){
            res.add(new ArrayList<>(path));
            return;
        }

        if(root.left != null){
            path.addLast(root.left.val);
            backtracking(root.left,targetSum,sum + root.left.val);
            path.removeLast();
        }
        if(root.right != null){
            path.addLast(root.right.val);
            backtracking(root.right,targetSum,sum + root.right.val);
            path.removeLast();
        }
    }
}

看了官方题解以后发现自己的代码写的很繁琐，修改后的代码：

class Solution {

    List<List<Integer>> res = new ArrayList<>();
    Deque<Integer> path = new ArrayDeque<>();
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        backtracking(root,targetSum);
        return res;
    }

    public void backtracking(TreeNode root,int sum){
        if(root == null) return;

        path.addLast(root.val);
        sum -= root.val;

        // 有答案时还要判断是否是叶子节点
        if(sum == 0 && root.left == null && root.right == null){
            res.add(new ArrayList<>(path));
            // return;
            // 这里不能加return 如果加了return就会影响弹栈
        }

        backtracking(root.left,sum);
        backtracking(root.right,sum);
        path.removeLast();
    }
}

3、最近的公共祖先 ✔

二叉搜索树最近的公共祖先

由于是二叉搜索树，左子树的最大值永远小于根节点，右子树的最小值永远大于根节点，很容易想到判断p、q两点的落点，再进行递归。

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(p.val>root.val && q.val>root.val)    //都在右子树  递归右子树
            return lowestCommonAncestor(root.right,p,q);
        if(p.val<root.val && q.val<root.val)     //都在左子树   递归左子树
            return lowestCommonAncestor(root.left,p,q);
        return root;      //其他情况都是return root
    }

复杂度分析:

• 时间复杂度: O(N) ，其中 N 是树的节点数。对每个节点访问一次。
• 空间复杂度: O(H) H为树的高度，空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 (logN)。

二叉树的公共祖先

这道题跟上面就只有搜索树的区别，首先想到的也是递归，
p q的落点只有三种情况：二左/二右/一左一右

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || p == root || q == root) return root;
        TreeNode l = lowestCommonAncestor(root.left,p,q);
        TreeNode r = lowestCommonAncestor(root.right,p,q);
        if(l == null && r == null) return null;
        if(l == null) return r; // 如果在左子树中 p和 q都找不到，则 p和 q一定都在右子树中，
        						//右子树中先遍历到的那个就是最近公共祖先
        else if(r == null) return l; // 否则，如果 left不为空，在左子树中有找到节点（p或q），
        							//这时候要再判断一下右子树中的情况，如果在右子树中，p和q都找不到，则 p和q一定
        							//都在左子树中，左子树中先遍历到的那个就是最近公共祖先
        else return root; //否则，当 left和 right均不为空时，说明 p、q节点分别在 root异侧
    }

复杂度分析:

• 时间复杂度: O(N) ，其中 N 是树的节点数，最差情况下需要对每个节点访问一次。
• 空间复杂度: O(H) H为树的高度，空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 (logN)。

4、二叉树的三种遍历-递归非递归 ✔

二叉树的前序遍历

递归方法:

class Solution {
    List<Integer> res = new ArrayList<>();    //定义在外部 才不会因为递归被重复定义
    										  //看答案都是重新定义一个方法,我这应该算偷懒了
    public List<Integer> preorderTraversal(TreeNode root) {
        if(root != null){
            res.add(root.val);
            preorderTraversal(root.left);
            preorderTraversal(root.right);
        }
        return res;
    }
}

非递归方法:
实际上非递归的方法也是模拟递归的套路，递归用的是系统栈，而迭代的方法则是自己定义一个Stack来模拟递归的压栈。

public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        if (root == null) return res;
        
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        TreeNode node = root;
        while (!stack.isEmpty() || node != null) {
            while (node != null) {
                res.add(node.val);
                stack.push(node);   //将该节点压栈,用于待会访问右节点
                node = node.left;   
            }
            node = stack.pop();
            node = node.right;
        }
        return res;
    }

复杂度分析:

• 时间复杂度: O(N) ，其中 N 是二叉树的节点数。每一个节点恰好被遍历一次。
• 空间复杂度: O(H) ， H为树的高度，空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 (logN)。

二叉树的中序遍历

因为递归的方法代码都相同，所以下面只研究非递归方法的代码

非递归方法:

public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root == null) return res;

        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode cur = root;
        while(!stack.isEmpty() || cur != null){
            while(cur != null){
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.pop();
            res.add(cur.val);      //与前序遍历基本相同,只是把添加root的值的步骤放到了这里
            cur = cur.right;
            System.out.println(res);
        }
        return res;
    }

二叉树的后序遍历

非递归方法:
后序遍历和前序中序有所不同，看了题解之后有两种解法：

解法一：
因为后序遍历的顺序是 左–>右–>中，可以利用双向链表，当我们遍历的顺序是 中–>右–>左 时， 遍历后将结果插入链表的头部而非尾部，那么结果链表就变为了：左–>右–>中，正好就是我们想要的顺序

基于这两个思路，我们想一下如何处理：

• 修改前序遍历代码中，节点写入结果链表的代码，将插入队尾修改为插入队首
• 修改前序遍历代码中，每次先查看左节点再查看右节点的逻辑，变为先查看右节点再查看左节点

理清逻辑之后代码如下：

public List<Integer> postorderTraversal(TreeNode root) {
        LinkedList<Integer> res = new LinkedList<>();  //这里相较于前序中序遍历换成了LinkedList，其它地方基本没有变化
        if(root == null) return res;

        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode cur = root;
        while(cur != null || !stack.isEmpty()){
            while(cur != null){
                res.addFirst(cur.val);
                stack.push(cur);
                cur = cur.right;
            }
            cur = stack.pop();
            cur = cur.left;
        }
        return res;
    }

解法二：
还是类似前序中序的代码，但是因为弹栈的问题无法将根节点的值在最后再添加，所以如果遍历到右节点时如果右节点不为空 则将根节点再次压栈

递归、回溯、分治

回溯三部曲:

1. 确定参数、返回值
2. 确定终止条件
3. 确定单层搜索逻辑

1、n皇后 ✔

n皇后

经典回溯题

代码:

class Solution {

    List<List<String>> res = new ArrayList<>();
    List<String> path = new ArrayList<>();
    public List<List<String>> solveNQueens(int n) {
        backTracking(n, 0);
        return res;
    }

    void backTracking(int n, int row) {
        if(row == n) {
            res.add(new ArrayList<>(path));
            return;
        }

        char[] line = new char[n];
        Arrays.fill(line, '.');
        // 同一层为同一行的不同选择
        for(int col = 0; col < n; col++) {
            if(isVaild(n, row, col)) {   // 验证可以放Queen
                // 做出选择
                line[col] = 'Q';
                path.add(new String(line));

                backTracking(n, row + 1);

                // 撤销选择
                line[col] = '.';
                path.remove(path.size() - 1);
            }
        }
    }

    boolean isVaild(int n, int row, int col) {
        // 检查列
        for(int i = 0; i < row; i++) {
            if(path.get(i).charAt(col) == 'Q') return false;
        }

        // 检查左上角一条线
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
             if (path.get(i).charAt(j) == 'Q') return false; 
        }

        // 检查右上角一条线
        for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
             if (path.get(i).charAt(j) == 'Q') return false; 
        }

        return true;
    }
}

n皇后 II

class Solution {

    int count = 0;
    List<String> path = new ArrayList<>();
    public int totalNQueens(int n) {
        backTracking(n, 0);
        return count;
    }

    void backTracking(int n, int row) {
        if(row == n) {
            count++;
            return;
        }

        char[] line = new char[n];
        Arrays.fill(line, '.');
        for(int col = 0; col < n; col++) {
            if(isValid(n, row, col)) {
                // 做出选择
                line[col] = 'Q';
                path.add(new String(line));
                backTracking(n, row + 1);
                // 撤销选择
                line[col] = '.';
                path.remove(path.size() - 1);
            }
        }
    }

    boolean isValid(int n, int row, int col) {
        // 验证列合法
        for(int i = 0; i < row; i++) {
            if(path.get(i).charAt(col) == 'Q') return false;
        }

        // 验证左上角一条线
        for(int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if(path.get(i).charAt(j) == 'Q') return false;
        }

        // 验证右上角一条线
        for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
            if(path.get(i).charAt(j) == 'Q') return false;
        }

        return true;
    }
}

2、生成括号 ✔

括号生成

思路：

1. 不需要用到循环，如果左括号数量不大于 n，我们可以放一个左括号。如果右括号数量小于左括号的数量，我们可以放一个右括号。

代码：

List<String> res = new ArrayList<>();
    public List<String> generateParenthesis(int n) {
        StringBuilder path = new StringBuilder();
        backtracking(path,n,0,0);
        return res;
    }

    public void backtracking(StringBuilder path,int n,int left,int right){
        if(path.length() == n*2){
            res.add(path.toString());
            return;
        }
            
        if(left < n){
            path.append("(");
            backtracking(path,n,left + 1,right);
            path.deleteCharAt(path.length() - 1);
        }
        if(right < left){      //这一步很重要
            path.append(")");
            backtracking(path,n,left,right + 1);
            path.deleteCharAt(path.length() - 1);
        }
        
    }

3、求子集I II ✔

子集

思路:

• 常规的回溯题目，但是需要注意的是终止条件的定义，因为题目要求的是返回所有集合，所以其实并不需要加上判断和return，就可以完成

代码：

List<List<Integer>> res = new ArrayList<>();
    Deque<Integer> path = new ArrayDeque<>();
    public List<List<Integer>> subsets(int[] nums) {
        if(nums.length == 0) return res;
        backtracking(nums,0);
        return res;
    }

    // 定义参数 返回值
    public void backtracking(int[] nums,int startIndex){
        // 定义终止条件  这里并不需要定义终止条件
        res.add(new ArrayList<>(path));


        // 定义单层搜索逻辑
        for(int i = startIndex;i < nums.length;i++){
            path.addLast(nums[i]);
            backtracking(nums,i + 1);
            path.removeLast();
        }
    }

子集 II

思路：

• 常见的套路，只需要先把数组排序 再在单层搜索逻辑中判断是否与前一位相同，如果相同跳过这次循环即可

代码：

List<List<Integer>> res = new ArrayList<>();
    Deque<Integer> path = new ArrayDeque<>();
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        backtracking(nums,0);
        return res;
    }

    public void backtracking(int[] nums,int startIndex){
        res.add(new ArrayList<>(path));

        for(int i = startIndex;i < nums.length;i++){
            if(i > startIndex && nums[i] == nums[i-1]) continue;

            path.addLast(nums[i]);
            backtracking(nums,i + 1);
            path.removeLast();
        }
    }

4、组合数之和 ✔

组合总和

思路:

1. 使用回溯法，先确定参数：int[] candidates ， int target ， int sum，int startIndex ， 但是通过观察发现我们可以使用 target - candidates[i] 来代替 sum 的作用，所以参数确定为 int[] candidates ， int target ，int startIndex
2. 终止条件确定为：
   当 target - candidates[i] < 0 时，则这时的总和已经超过target，直接return
   当 target - candidates[i] == 0 时，这时的总和正好等于target，将path存入res中，return
3. 单层循环逻辑确定为：
   backtracking(candidates,target-candidates[i],i);
   因为数组中的数字可以重复使用，所以下一次搜索依旧从 i 开始
4. 剪枝操作：
   先将数组排序（这是剪枝前提）
   当 进入循环时 target - candidates[i] 已经 < 0 了 ， 我们就不用再将这个循环继续下去了，直接break

代码：

	List<List<Integer>> res = new ArrayList<>();
    Deque<Integer> path = new ArrayDeque<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        backtracking(candidates,target,0);
        return res;
    }

    //1.确定返回值,参数
    public void backtracking(int[] candidates,int target,int startIndex){
        int n = candidates.length;
        //2.确定终止条件
        if(target < 0) return;
        if(target == 0){
            res.add(new ArrayList<>(path));
            return;
        }

        //3.确定单层循环逻辑     4.剪枝  
        for(int i = startIndex;i < n;i++){
            // 重点理解这里剪枝，前提是候选数组已经有序，
            if (target - candidates[i] < 0) {
                break;
            }

            path.addLast(candidates[i]);
            backtracking(candidates,target-candidates[i],i);
            path.removeLast();
        }


    }

组合总和 II

这道题几乎和上面一样，只限制了数组中的数字不能重复使用，并且答案集合中不能出现重复的数组

思路：

1. 确定参数返回值、确定终止条件，这两步都跟上一题一样
2. 确定单层搜索逻辑：
   在这里要加一个判断，判断当前这个元素是否跟上一个一样，如果一样那将会产生相同的结果，所以直接continue
   backtracking(candidates,target - candidates[i],i + 1);
   数组中的数字不可以重复使用，所以下一次搜索从 i + 1 开始
3. 剪枝操作：
   先将数组排序（这是剪枝前提）
   当 进入循环时 target - candidates[i] 已经 < 0 了 ， 我们就不用再将这个循环继续下去了，直接break

代码：

List<List<Integer>> res = new ArrayList<>();
    Deque<Integer> path = new ArrayDeque<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        if(candidates.length == 0) return res;
        Arrays.sort(candidates);
        backtracking(candidates,target,0);
        return res;
    }

    //确定参数 返回值
    public void backtracking(int[] candidates,int target,int startIndex){
        //确定终止条件
        if(target < 0) return;
        if(target == 0){
            res.add(new ArrayList<>(path));
            return;
        }

        //确定循环单层搜索逻辑
        for(int i=startIndex;i<candidates.length;i++){
            if(target - candidates[i] < 0) break;    //剪枝
            /*这个if判断，保证了解集不包含重复组合
            只要数组中索引i处的值 等于 它前一个索引的值，就直接continue跳过*/
            if(i > startIndex && candidates[i] == candidates[i-1]) continue;
            path.addLast(candidates[i]);
            backtracking(candidates,target - candidates[i],i + 1);
            path.removeLast();
        }

    }

5、岛屿问题 ✔

岛屿类问题的通用解法、DFS框架

岛屿的最大面积

思路：

这道题目只需要对每个岛屿做 DFS 遍历，求出每个岛屿的面积就可以了。求岛屿面积的方法也很简单，每遍历到一个格子，就把面积 + 1，代码如下：

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        int res = 0;
        for(int i = 0; i < grid.length; i++){
            for(int j = 0;j < grid[0].length; j++){
                if(grid[i][j] == 1){
                    int temp = area(grid,i,j);
                    res = Math.max(res,temp);
                }
            }
        }
        return res;
    }

    public int area(int[][] grid,int i,int j){
        // 判断是否在区域内
        if(!inArea(grid,i,j)) return 0;
        // 判断是否是未走过的陆地
        if(grid[i][j] != 1) return 0;
        // 如果是陆地就将1改为2
        grid[i][j] = 2;

        return   1
                +area(grid,i+1,j)
                +area(grid,i-1,j)
                +area(grid,i,j+1)
                +area(grid,i,j-1);
    }

    public boolean inArea(int[][] grid,int i,int j){
        return i < grid.length && i >= 0 && j >= 0 && j < grid[0].length; 
    }
}

岛屿数量

思路：
每次遍历到 grid[i][j] 就按照dfs思路遍历并将 grid[i][j] = 2

代码：

class Solution {
    public int numIslands(char[][] grid) {
        int res = 0;
        for(int i = 0; i < grid.length; i++){
            for(int j = 0; j < grid[0].length; j++){
                if(grid[i][j] == '1'){
                    dfs(grid,i,j);
                    res++;
                }
            }
        }
        return res;
    }

    public void dfs(char[][] grid,int i,int j){
        if(!inArea(grid,i,j)) return;
        if(grid[i][j] == '0') return;
        if(grid[i][j] != '1') return;

        grid[i][j] = '2';
        dfs(grid,i+1,j); 
        dfs(grid,i-1,j); 
        dfs(grid,i,j+1); 
        dfs(grid,i,j-1); 
    }

    public boolean inArea(char[][] grid,int i,int j){
        return i >= 0 && j >= 0 && i < grid.length && j < grid[0].length;
    }
}

最大人工岛

思路：

• 先dfs遍历一次，求出每一块陆地的面积，并且把不同的陆地打上不同的编号
• 用HashMap将陆地的编号 面积存起来
• 再次遍历，这次遍历要找到每一块海洋，然后假设这个格子填充，把上下左右是陆地的格子所在的岛屿连接起来
• 使用findneighbour方法找到上下左右的陆地邻居，并且这里需要用HashSet存储去重

// 对于海洋格子，找到上下左右
    // 每个方向，都要确保有效inArea以及是陆地格子，则表示是该海洋格子的陆地邻居  
    public HashSet<Integer> findNeighbour(int[][] grid,int i,int j){
        HashSet<Integer> set = new HashSet();
        if(inArea(grid,i+1,j) && grid[i+1][j] != 0){
            set.add(grid[i+1][j]);
        }
        if(inArea(grid,i-1,j) && grid[i-1][j] != 0){
            set.add(grid[i-1][j]);
        }
        if(inArea(grid,i,j+1) && grid[i][j+1] != 0){
            set.add(grid[i][j+1]);
        }
        if(inArea(grid,i,j-1) && grid[i][j-1] != 0){
            set.add(grid[i][j-1]);
        }
        return set;
    } 

• 遍历set取出 index 再找对应的面积 求出total，遍历完成return最大的total

完整代码：

class Solution {
    public int largestIsland(int[][] grid) {
        int res = 0, index = 2; // 因为陆地为1 所以标记从2开始
        HashMap<Integer,Integer> areas = new HashMap();
        // 遍历求出每块陆地的面积，并打上编号
        for(int i = 0; i < grid.length; i++){
            for(int j = 0; j < grid[0].length; j++){
                if(grid[i][j] == 1){
                    int temp = area(grid,i,j,index);   // 每次dfs的面积
                    areas.put(index,temp);     // 将编号 面积存入hashmap
                    res = Math.max(res,temp);   // 将最大值存入res
                    index++;
                }
            }
        }

        if(res == 0) return 1;   // 如果res = 0 说明没有陆地，返回1

        // 再次遍历，这次遍历要找到每一块海洋，然后假设这个格子填充，把上下左右是陆地的格子所在的岛屿连接起来
        for(int i = 0; i < grid.length; i++){
            for(int j = 0; j < grid[0].length; j++){
                if(grid[i][j] == 0){
                    HashSet<Integer> set = findNeighbour(grid,i,j);  // 接受findNeighbour传过来的set
                    if (set.size() < 1) continue;    // 如果海洋格子周围没有格子不必计算
                    int total = 1;      // 填充这个格子，初始为1，这个变量记录合并岛屿后的面积
                    for(Integer k : set){
                        total += areas.get(k);  // 把面积加上
                    }
                    res = Math.max(res,total);  // 比较得到最大的面积
                }
            }
        }

        return res;
    }


    // 对于海洋格子，找到上下左右
    // 每个方向，都要确保有效inArea以及是陆地格子，则表示是该海洋格子的陆地邻居  
    public HashSet<Integer> findNeighbour(int[][] grid,int i,int j){
        HashSet<Integer> set = new HashSet();
        if(inArea(grid,i+1,j) && grid[i+1][j] != 0){
            set.add(grid[i+1][j]);
        }
        if(inArea(grid,i-1,j) && grid[i-1][j] != 0){
            set.add(grid[i-1][j]);
        }
        if(inArea(grid,i,j+1) && grid[i][j+1] != 0){
            set.add(grid[i][j+1]);
        }
        if(inArea(grid,i,j-1) && grid[i][j-1] != 0){
            set.add(grid[i][j-1]);
        }
        return set;
    } 


    public int area(int[][] grid,int i,int j,int index){
        if(!inArea(grid,i,j) || grid[i][j] == 0) return 0;
        if(grid[i][j] != 1) return 0;  // 说明已经走过这块地

        grid[i][j] = index;        // 标记陆地
        return   1 
                +area(grid,i+1,j,index)
                +area(grid,i-1,j,index)
                +area(grid,i,j+1,index)
                +area(grid,i,j-1,index);
    }

    public boolean inArea(int[][] grid,int i,int j){
        return i >= 0 && j >= 0 && i < grid.length && j < grid[0].length;
    }
}