数据结构与算法分析-C++描述 第9章 图论算法（无向图之广度优先搜索和深度优先探索）

基本概念（basic conception）：

        1）图（graph）：由边的集和顶点的集构成。如果点对是有序的，则称为有向图（digraph）。在一个具有边从而具有边的有向图中，与邻近且与邻近。

        如果在无向图中，从每一个顶点到其他顶点都存在一条路径，则称该无向图是连通的（connected）。具有这种性质的有向图称为强连通的（strongly connected），如果有向图的基础图（underlying graph）（对应的无向图）是连通的，则称有向图弱连通的（weakly connected）。

        完全图（complete graph）是每一对顶点都存在一条路径的图。

        2）图的表示（expression）：

                2.1）邻接矩阵（adjacent matrix）：对每条边，置，否则为。

                2.2）邻接表（adjacent list）：对每个顶点，使用一个表存放所有邻接的顶点。

               空间需求：邻接矩阵：，若矩阵是稠密的，则邻接矩阵表示是合适的，否则使用空间需求为的邻接表。

        3）最短路径：

                3.1）加权路径：输入一个加权图，与每条边相联系的穿越该边的代价为，一条路径的值是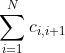叫做加权路经长（weighted path length）

                3.2）无权路径：无权路径长只是路径的边数。

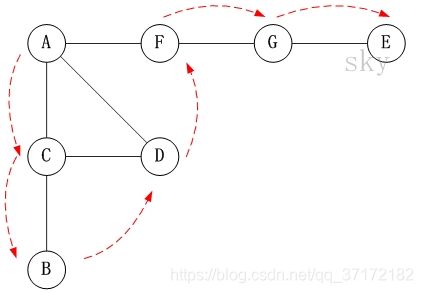
广度优先搜索算法（Breadth First Search）：

       从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。

深度优先探索算法（Depth First Search）：

        假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

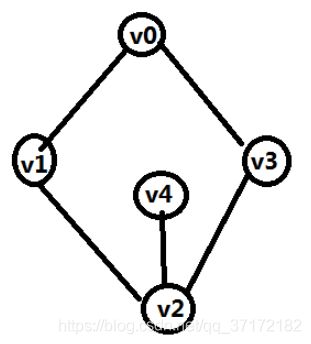
实例：建立如下无向图，设计DFS和BFS算法打印遍历结果。

 

//main.cpp
#include
#include
#include
#include

using namespace std;
const int N = 10;
vector visited(N);

struct EdageNode{
	int adjointVertex;
	EdageNode *next;
	
	//EdageNode constructor
	EdageNode(int a = 0, EdageNode *n = NULL):adjointVertex(a), next(n){
	
	};
};

struct AdjointList{
	string data;
	EdageNode *firstEdage;
};

struct Graph{
	int numVertex;
	int numEdge;
	vector adjointList;
	
	//Graph constructor
	Graph(int n = 10):adjointList(n){
	};
};

//create Graph g
void createGraph(Graph &g);

//get value's position in g
int getPosition(Graph g, string value);

//print the graph
void print(Graph g);

//Depth First Search for Graph g with index i
void DFS(Graph g, int index);

//Depth First Search Traverse
void DFSTraverse(Graph g);

//Breadth First Search Traverse
void BFSTraverse(Graph g);

//destroy Graph g
void destroyGraph(Graph &g);

int main(){
	Graph g;
	cout << "*********** createGraph *************" << endl;
	createGraph(g);
	cout << "*********** printGraph *************" << endl;
	print(g);
	cout << "*********** DFSTraverse *************" << endl;
	DFSTraverse(g);
	cout << "*********** BFSTraverse *************" << endl;
	BFSTraverse(g);
	cout << "*********** destroyGraph *************" << endl;
	destroyGraph(g);
	cout << " done ." << endl;
	return 0;
}

void createGraph(Graph &g){
	cout << "Enter the num of vertex and edage splited with space : " << endl;
	cin >> g.numVertex >> g.numEdge;
	cout << "Please enter the vertex info : " << endl;
	for(int i = 0; i < g.numVertex; i++){
		cout << i + 1 << "th vertex is : ";
		cin >> g.adjointList[i].data;
		g.adjointList[i].firstEdage = NULL;
	}
	int pos1, pos2;
	string data1, data2;
	EdageNode *node;
	EdageNode *temp;
	for(int i = 0; i < g.numEdge; i++){
		cout << "Please enter the edage (v_i, v_j) info : ";
		cin >> data1 >> data2;
		pos1 = getPosition(g, data1);
		pos2 = getPosition(g, data2);
		//data1's firstEdage is NULL or not
		if(g.adjointList[pos1].firstEdage == NULL){		//yes, connect data2 to data1 rear
			node = new EdageNode(pos2, NULL);
			g.adjointList[pos1].firstEdage = node;		
		}else{											//no, connect data2 to data1 until data1's next is NULL
			temp = g.adjointList[pos1].firstEdage;
			while(temp -> next != NULL){
				temp = temp -> next;
			}
			node = new EdageNode(pos2, NULL);
			temp -> next = node;
		}
		//data2's firstEdage is NULL or not
		if(g.adjointList[pos2].firstEdage == NULL){  	//yes, connect data1 to data2 rear
			node = new EdageNode(pos1, NULL);
			g.adjointList[pos2].firstEdage = node;
		}else{											//no, connect data1 to data2 until data2's next is NULL
			temp = g.adjointList[pos2].firstEdage;
			while(temp -> next != NULL){
				temp = temp -> next;
			}
			node = new EdageNode(pos1, NULL);
			temp -> next = node;
		}
	}
}

int getPosition(Graph g, string value){
	for(int i = 0; i < g.numVertex; i++){
		if(g.adjointList[i].data == value){
			return i;
		}
	}
	return -1;
}

void print(Graph g){
	cout << " The Graph constructed by adjointList as follows : " << endl;
	for(int i = 0; i < g.numVertex; i++){
		cout << g.adjointList[i].data;
		//access each data and find its next data
		EdageNode *node = g.adjointList[i].firstEdage;
		while(node){
			cout << " --> " << node -> adjointVertex;
			node = node -> next; 
		}
		cout << endl;
	}
}

void DFS(Graph g, int index){
	EdageNode *node;
	visited[index] = true;
	cout << g.adjointList[index].data << " ";
	node = g.adjointList[index].firstEdage;
	//access data until the node is NULL
	while(node){
		if(!visited[node -> adjointVertex]){
			DFS(g, node -> adjointVertex);
		}
		node = node -> next;
	}
}

void DFSTraverse(Graph g){
	for(int i = 0; i < g.numVertex; i++){
		visited[i] = false;
	}
	for(int i = 0; i < g.numVertex; i++){
		if(!visited[i]){
			DFS(g, i);
		}
	}
	cout << endl;
}

void BFSTraverse(Graph g){
	EdageNode *node;
	queue bfsQueue;
	vector visited(g.numVertex);
	for(int i = 0; i < g.numVertex; i++){
		visited[i] = false;
	}
	for(int i = 0; i < g.numVertex; i++){
		if(!visited[i]){
			visited[i] = true;
			cout << g.adjointList[i].data << " ";
			bfsQueue.push(i);
			while(!bfsQueue.empty()){
				int count = bfsQueue.front();
				bfsQueue.pop();
				node = g.adjointList[i].firstEdage;
				//access firstEdage until node is NULL
				while(node){
					if(!visited[node -> adjointVertex]){
						visited[node -> adjointVertex] = true;
						cout << g.adjointList[node -> adjointVertex].data << " ";
						bfsQueue.push(node -> adjointVertex);
					}
					node = node -> next;
				}
			}
		}
	}
	cout << endl;
}

void destroyGraph(Graph &g){
	EdageNode *temp = NULL;
	for(int i = 0; i < g.numVertex; i++){
		temp = g.adjointList[i].firstEdage;
		while(temp){
			EdageNode *node = temp;
			temp = temp -> next;
			delete node;
		}
		g.adjointList[i].firstEdage = NULL;
	}
}

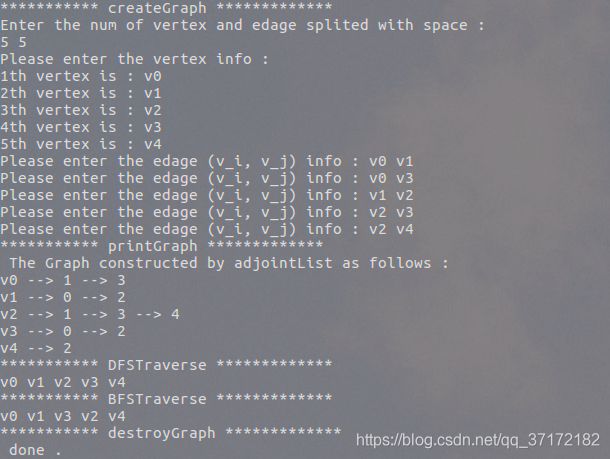
运行结果：

practice makes perfect ！