一文彻底搞懂LRU缓存结构的实现

什么是LRU缓存结构

所谓LRU缓存（Least Recently Used cache）是指大小固定的一块内存空间，同时要求实现以下两个功能。

（1）set(key,value)：将记录(key,value)插入LRU缓存结构。

（2）get(key)：返回关键字key对应的value值。

并且LRU缓存必须满足以下要求：

（1）set()方法和get()方法的时间复杂度均为O(1)。

（2）每执行一次set()操作或者get()操作，操作的记录将变成“最常使用记录”。

（3）当缓存的大小超过最大限度时，要移除“最不常使用的记录”，也就是最久没有被执行set()或get()的记录。

说得直白一点，LRU缓存就是一个高速缓存结构，在缓存中读取或写入数据的效率要尽量的高，要求达到O(1)；同时因为这个缓存大小是固定的，因此当缓存已满时就需要一个“缓存页替换策略”，这个策略就是将最不常使用的记录替换掉。举例说明：有一个LRU缓存的容量为4，依次进行如下操作后LRU的状态如表1所示。

表1  LRU状态变化

set()或get()操作	LRU的状态
set(‘A’,1)	LRU中只有1个记录，最常使用记录就是(‘A’,1)
set(‘B’,2)	LRU中有2个记录，最常使用记录变为(‘B’,2)，最不常使用记录为(‘A’,1)
get(‘A’)	LRU中有2个记录，最常使用记录变为(‘A’,1)，最不常使用记录变为(‘B’,2)
set(‘C’,3)	LRU中有3个记录，最常使用记录变为(‘C’,3)，最不常使用记录仍为(‘B’,2)
set(‘D’,4)	LRU中有4个记录，最常使用记录变为(‘D’,4)，最不常使用记录仍为(‘B’,2)
get(‘B’)	LRU中有4个记录，最常使用记录变为(‘B’,2)，最不常使用记录变为(‘A’,1)
set(‘E’,5)	超过LRU容量4，移除最不常使用记录(‘A’,1)，然后插入(‘E’,5)，此时最常使用记录变为(‘E’,5)，最不常使用记录变为(‘C’,3)

​如何实现LRU缓存结构

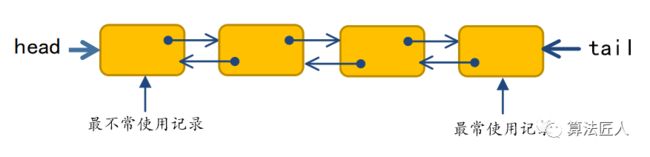
首先我们来考虑如何实现缓存淘汰策略。因为缓存中插入和删除数据的操作会非常频繁，所以不应使用数组（顺序表）来实现。单链表结点的插入和删除固然复杂度较低，但是由于在LRU缓存中需要经常调整数据记录的顺序（用以确定哪些数据是最常使用，哪些数据是最不常使用），所以单链表操作也不是很便捷。所以通常使用双向链表作为缓存中数据的载体。对于LRU缓存，可规定双向链表的表头（head）保存“最不常使用的记录”，表尾（tail）保存“最常使用的记录”。

当执行set()操作将一条记录插入LRU缓存时，可将该数据结点插入到双向链表的表尾tail，此时该记录就是“最常使用的记录”。

当执行get()操作从LRU缓存中读取一个记录时，除了找到包含该记录的链表结点并将其返回之外，同时还要将该结点调整到双向链表的尾部，使其成为“最常使用的记录”。

当执行set()操作将一条记录插入LRU缓存，但此时LRU缓存已到达最大容量时，可将双向链表的表头head结点移除，因为表头head为“最不常使用的记录”。

下面给出构成LRU缓存的双向链表类的定义。

class Node {
  public V data;
  public Node prior;   //指向前驱结点的指针
  public Node next;    //指向后继结点的指针
  public Node(V data) {
    this.data = data;     //结点中的数据
  }
}
​
class DoubleLinkedList {
  private Node head;  //双向链表的表头
  private Node tail;  //双向链表的表尾
  
  public DoubleLinkedList() {
    this.head = null;
    this.tail = null;
  }
​
  //向链表的尾部插入结点，使其成为“最常使用记录”
  public void addNode(Node node) {
    if (node == null) {
      return false;
    }
    
    if (head == null) {
      //双向队列为空
      head = node;
      tail = node;
    } else {
      tail.next = node;   //将node插入到队列尾部
      node.prior = tail;  //建立相互连接
      tail = node;         //修改tail指针
    }
    return true;
  }
  
//将链表中的结点node移到链表尾部，使其成为“最常使用记录”
  public void moveNodeToTail(Node node) {
    if (tail == node) {
      //要移动的结点是tail位置上的结点
      return;     //不需要任何操作
    }
    
    if(head == node) {
      //要移动的结点是head位置上的结点
      head = node.next;
      head.prior = null;    //将node结点删除
    }else {
      //要删除的结点是链表中间的某结点
      node.prior.next = node.next;
          node.next.prior = node.prior;   //将node结点删除      
    }
    
    //将删除了的node结点插入到tail位置
    node.prior = tail;
    node.next = null;
    tail.next = node;
    tail = node;
  }
​
//删除表头结点，即移除“最不常使用记录”
  public Node removeHead() {
    if (head == null) {
      //链表中没有结点
      return null;
    }
    
    Node res = head;  //res指向头结点
    if (head == tail) {
      //链表中仅有一个结点,将head和tail置为null
      head = null;
      tail = null;
    } else {
      //删除head结点，head指向原头结点的后继结点
      head = res.next;
      res.next = null;
      head.prior null;
    }
    return res;
  }
}

首先定义了双向链表的结点类Node。为了使其具有通用性，这里不指定结点数据的类型，而采用泛型定义Node，V表示结点数据的类型（可以是任意引用类型，例如Integer，Character等）。

双向链表类DoubleLinkedList也采用泛型定义，V是链表结点数据的类型。在DoubleLinkedList类中定义了两个成员变量，Node head是指向双向链表的表头，即最不经常使用的记录，Node tail指向双向链表的表尾，即最常使用的记录。如图1-1所示。

图1 LRU缓存结构的双向链表实现

此外还定义了三个成员方法，分别执行以下三个不同的操作。

（1）void addNode(Node node)：向链表的尾部插入结点，使其成为“最常使用记录”。

（2）void moveNodeToTail(Node node)：将链表中的结点node移到链表尾部，使其成为“最常使用记录”。

（3）Node removeHead()：删除表头结点，也就是移除“最不常使用记录”。

以上定义的双向链表类和基本操作构成了LRU缓存的基础数据结构。

下面要考虑的第二个问题就是如何尽可能高效地在缓存中读取和写入数据，本题的要求是set()方法和get()方法的时间复杂度均为O(1)。对于set()方法，可通过调用DoubleLinkedList类的addNode()方法将结点插入双向链表的尾部，这个时间复杂度本身就是O(1)。而对于get()方法，则需要通过给定的记录的关键字key找到该记录并返回。如何在O(1)的时间复杂度内完成这个相对复杂的操作呢？最常用的方法是使用HashMap帮助实现O(1)复杂度的查找功能。

这里可以使用两个HaspMap将关键字key和双向链表中的结点node一一对应起来。其中一个HaspMap中以key作为关键字，这样可以通过指定的key在O(1)的时间内找到对应的结点引用node，也就是在双向链表上建立一个索引；另一个HashMap中以node作为关键字，这样可以通过给定的node在O(1)的时间内找到该结点对应的key，它的作用主要是为了在删除双向链表中的结点时可以找到对应的key，从而删除HashMap中的索引。有了这两个HashMap的帮助就可以在O(1)的时间复杂度内定位到双向链表中的结点，从而进行插入、删除等各种操作。下面给出LRU Cache的定义。

public class LRUCache {
  private DoubleLinkedList doubleLinkedList; //双向链表
  private HashMap,K> nodeKeyMap; //(node,key) map
  private HashMap> keyNodeMap; //(key,node) map
  private int capacity;
  
  public LRUCache(int capacity) {
    keyNodeMap = new HashMap>();
    nodeKeyMap = new HashMap,K> ();
    doubleLinkedList = new DoubleLinkedList();
    this.capacity = capacity;
  }
  
  public V get(K key) {
    //通过key获取LRU中的数据，并返回
    if (keyNodeMap.containsKey(key)) {
      Node res = keyNodeMap.get(key); //获取该结点在链表中的指针
      doubleLinkedList.moveNodeToTail(res);  //把该结点移到队列尾部，变为最常访问结点
      return res.value;
    }
    return null;
  }
  
  public void set(K key, V value) {
    if (keyNodeMap.containsKey(key)) {
      //如果set的(key,value)已存在与LRU中，此时就相当于更新value的操作
      Node node = keyNodeMap.get(key);    //通过keyNodeMap获取key对应的结点引用
      node.data = value;                     //将value赋值给结点数据node.data
      doubleLinkedList.moveNodeToTail(node); //将结点node移到链表尾部
    } else {
      //插入一个新的结点
      Node node = new Node(value);      //创建一个新的结点
      keyNodeMap.put(key,node);               //将(key,value)加入到keyNodeMap中
      nodeKeyMap.put(node,key);               //将(node,key)加入到nodeKeyMap中
      if (keyNodeMap.size() > capacity) {
        //LRU Cache移到到最大容量capacity，则删除“最不常使用记录”
                removeMostUnusedRecord();
      }
    }
  }
  
  private void removeMostUnusedRecord() {
    Node node = doubleLinkedList.removeHead();   //删除链表头部结点
    K key = nodeKeyMap.get(node);             //获取该结点对应的key
    nodeKeyMap.remove(node);                  //删除nodeKeyMap中这条记录的信息
    keyNodeMap.remove(key);                   //删除keyNodeMap中这条记录的信息
  }
}

LRUCache类可实现一个LRU缓存的功能。该类中的成员变量doubleLinkedList是一个DoubleLinkedList类型的双向链表（上面已给出定义），它是LRU缓存的主体，用来存放记录。成员变量nodeKeyMap为一个以结点node为关键字的HashMap，成员变量keyNodeMap为一个以key为关键字的HashMap，使用这两个HashMap可以对双向链表中的结点进行快速定位，从而提高在缓存中的查找效率。

在LRUCache类中还定义了题目要求的set()方法和get()方法。下面我们重点这两个方法的实现。

（1）V get(K key)方法

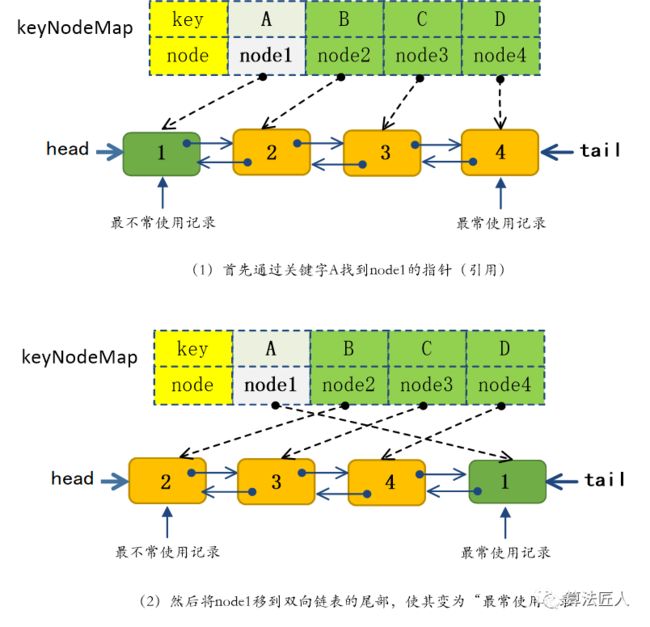
该方法的作用是通过指定的关键字key获取LRU中的数据并返回。在get()方法中，首先判断Hash表keyNodeMap中是否包含关键字key，如果包含则说明该记录已被保存在LRU缓存中（双向链表中存在该结点），此时调用DoubleLinkedList类的moveNodeToTail()方法将该结点移到链表尾部（表明该记录“最常使用”），然后将该结点中的数据data返回。图2所示为get(‘A’)的执行过程。

图2 get(‘A’)的执行过程

（2）void set(K key, V value)方法

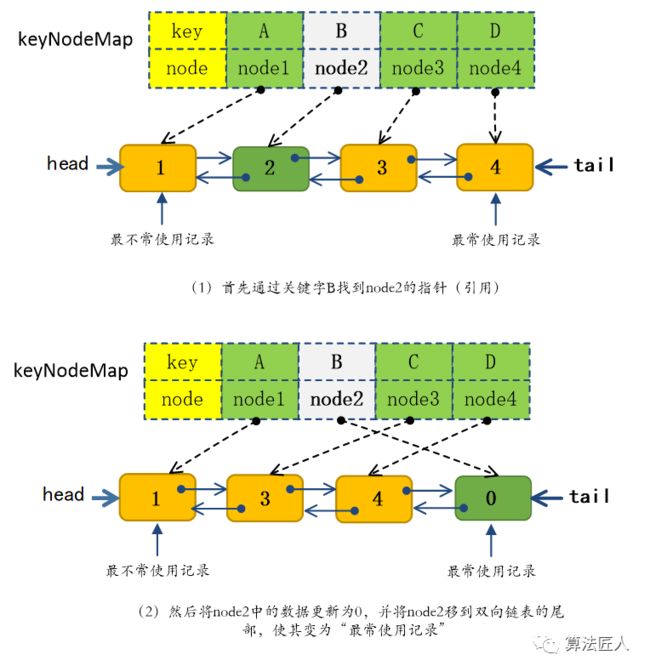
该方法的作用是将记录(key,value)插入LRU缓存。这里有两种情况需要考虑。情形1：如果Hash表keyNodeMap中已包含关键字key，则说明LRU缓存中已存在这条记录，此时相当于通过set()操作更新记录value。图3所示为set(‘B’,0)的执行过程。

图3 set(‘B’,0)的执行过程

如图3所示，首先通过keyNodeMap获取key对应的结点引用，然后将该结点中的数据域data更新为新值value，最后调用moveNodeToTail()方法将结点移到链表尾部（表明该记录“最常使用”）。

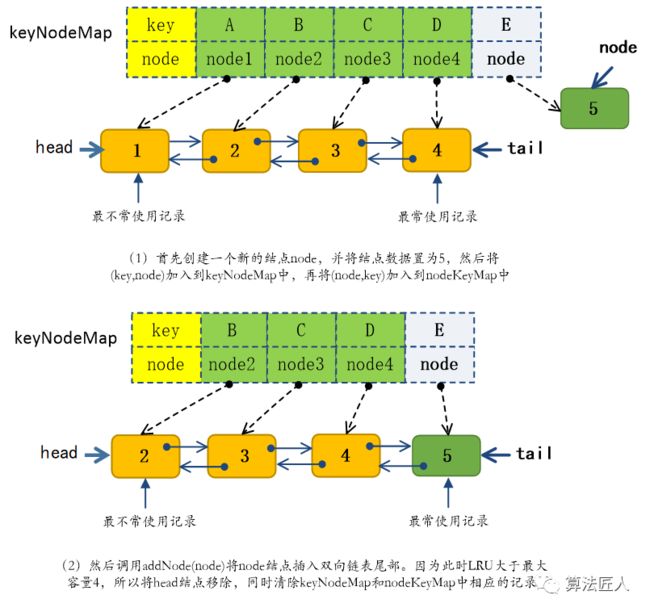
情形2：如果Hash表keyNodeMap中没有包含关键字key，则说明LRU缓存中还没有保存这条记录，此时先要创建以value为数据的链表结点实例node，然后将(key,node)加入到keyNodeMap中建立索引，再将(node,key)加入到nodeKeyMap中。最后调用DoubleLinkedList类的addNode()方法将新创建的结点插入到链表尾部（表明该记录“最常使用”）。如图4所示为set(‘E’,5)的执行过程。

图4 set(‘E’,5)的执行过程

需要注意的是，在执行set()操作时需要判断当前LRU缓存是否已达到最大容量capacity，如果将(key,node)加入到keyNodeMap中后keyNodeMap的size已大于capacity就说明此时LRU缓存已到达上限容量，这时要调用removeMostUnusedRecord()方法将双向链表的表头结点head移除，也就是移除掉”最不常使用的记录”。

这样就实现了一个LRU缓存的功能。在这个LRU缓存中，通过一个双向链表将数据记录进行保存，链表的头部head为最不常使用的记录，链表的尾部tail为最常使用的记录。通过Hash表keyNodeMap和nodeKeyMap实现索引的功能，将关键字key与双向链表中的结点构成一一对应的映射关系，从实现了set()方法和get()方法的时间复杂度均为O(1)。

有的同学可能会问：将双向链表中的结点移到tail的位置本身也会耗时啊?这个时间复杂度为O(n)为什么不算在set()和get()方法的时间复杂度中呢？这是因为在执行set()方法和get()方法的过程中，通过HashMap定位到双向链表中的结点的时间复杂度就是O(1)，此时即可返回结果或插入结点。而通过moveNodeToTail()方法将链表结点移动到链表尾部的操作本身属于LRU结构内部的调整工作，这些工作也完全可以单独放在一个线程中来完成，因此不应计入set()和get()的时间复杂度。

总结

这一讲我们我们介绍了经典的LRU缓存的设计方法。因为缓存的大小固定，所以需要设计一种缓存淘汰策略将“最不经常使用”的记录移除。因此在LRU缓存中就需要经常调整元素的位置，将最常使用的记录移到尾部（tail），将最不常使用的记录移到头部（head），所以将双向链表作为LRU缓存的存储体是最佳的选择。另外缓存的特点就是要快速读取和快速保存，为了达到O(1)时间复杂度的读写速度，我们必须借助HashMap工具给双向链表建立索引，以便快速定位数据记录。

想要阅读更多算法面试类精选文章，可关注我的微信公众号  @算法匠人

关注“算法匠人”微信公众号，共享“匠人的算法课”，我们一起提高进步。

 

---

--  算法匠人作品展示  --

向大家推荐《算法大爆炸：面试通关步步为营》一书。这本书是一本既可以帮助读者筑牢数据结构和算法基础，同时又能帮助读者提升职场竞争实力的书籍。