Can we learn better with hard samples

摘要

在深度学习中，小批量训练通常用于优化网络参数。然而，传统的小批处理方法可能无法学习到数据中代表性不足的样本和复杂的模式，从而导致泛化的时间更长。为了解决这一问题，提出了一种传统算法的一种变体，它训练网络集中于高损失的小批量。该研究使用在三个基准数据集（CIFAR-10、CIFAR-100和STL-10）上训练的各种深度神经网络来评估所提出的训练的有效性。本研究中使用的深度神经网络有ResNet-18、ResNet-50、高效Net B4、高效NetV2-S和MobilenetV3-S。实验结果表明，与传统的小批量训练方法相比，该方法能显著提高测试精度，加快收敛速度。此外，我们引入了一个超参数delta (δ)，它决定考虑多少小批次进行训练。对不同δ值的实验发现，该方法在较小的δ值下的性能通常具有相似的测试精度和更快的泛化速度。结果表明，在STL-10上，该方法比传统的小批量方法的训练轮数减少了26.47%。该方法还将CIFAR-100上的ResNet-18中测试前1的精度提高了7.26%。

介绍

多年来，深度神经网络（DNNs）在许多表示学习任务中脱颖而出。反向传播算法是训练神经网络的首选方法。反向传播算法允许多层神经网络学习输入和输出之间的复杂表示。它克服了在感知器等神经网络中学习线性可分离向量的局限性。本质上，数据越复杂，需要的反向传播就越多。深度学习领域已经从使用简单的人工神经网络学习简单的线性表示，到使用转换器学习高度复杂的细粒度表示，所有这些都使用反向传播。

神经网络中的反向传播算法可以批量应用（批量梯度下降）、每个样本（随机梯度下降）甚至小批量应用（小批量梯度下降）上应用。在批处理梯度下降算法中，反向传播是根据在数据集的所有样本上的梯度的平均值进行的。泛化需要大量的计算时间。随机梯度下降（SGD）算法在每次迭代中使用一个样本来计算梯度和更新权重。然而，SGD可能永远不会导致一个全局的最小值，而且网络可能不会收敛，因为梯度可能会被困在局部的最小值[8,36]上。小批梯度下降解决了这些问题，一个小批由固定数量的训练示例组成，但小于实际数据集的大小。因此，在每次迭代中，网络在不同的批处理组上进行训练，直到数据集中的所有样本都被使用。小批梯度下降比批梯度下降速度快，且卡在局部最小值的可能性较小。硬样本可能是那些在整个数据集中表示不足的样本，或者可能有一个复杂的表示，可能需要更多的迭代来学习。与数据集中的其他样本相比，这些样本可能需要更高的权重。这样的样本在反向传播后通常会导致较高的损失值。分配硬样本权重的最流行的算法方法之一是焦点损失。焦点损失的问题是，它有一个α和γ的超参数，这是在训练前决定的。

虽然反向传播算法使神经网络能够学习复杂的表示，但学习数据中的硬样本仍然是一个挑战。无法从数据集中学习硬样本的代价导致了收敛速度较慢。此外，神经网络倾向于有可约的误差，即偏差和方差。这个问题的一个众所周知的解决方案是增加网络的深度，从而提高网络泛化和学习更精细、更复杂的潜在表示的能力。从数据中的硬样本中学习是至关重要的，因为它可以提高训练网络的性能。从文献来看，深度神经网络减少方差和偏差通常收敛速度更快。近年来，神经网络已经被过度参数化，以克服可减少误差等限制。因此，研究能够提高神经网络泛化能力的方法是很重要的。作者认为，即使是更好的泛化的小进展也是一个重要的问题，将对深度学习领域产生很大的影响。

在本文中，作者提出了一种不同的小批量训练方法，重点是学习数据集中的硬样本。它的目的是与传统训练方法相比，帮助神经网络以最小的测试精度快速收敛。在这篇论文中，作者提出了一种小批量训练方法的变体，重点是学习数据集中的难样本。 它旨在帮助神经网络更快地收敛，同时相对于传统训练方法的测试精度变化最小。

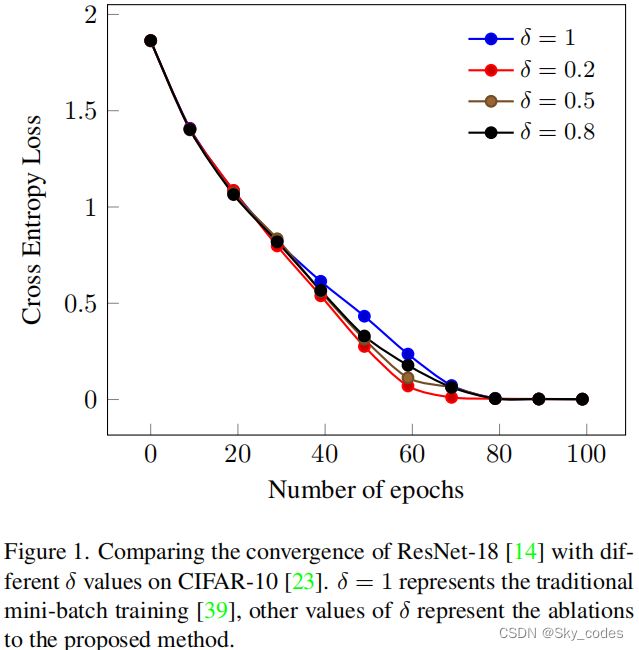
该方法背后的直觉是以下观察——在准备考试时，学生倾向于把更多的时间集中在困难的概念上，而不是简单的概念。该方法引入了一种新的超参数δ，它选择了一部分被认为是硬小批次的小批次，用于训练过程中的下一次迭代。作者将硬小批次定义为按损失值不递增顺序排列的小批次。对于选择一个小批的过程，δ可以从(0,1]中取值，其中1对应于对所有小批的选择。例如，δ值0.2、0.5、0.8、1对应于选择20%、50%、80%、80%和100%的小批次。图1显示，在CIFAR-10数据集[23]上，不同的δ值有助于ResNet 18 的加速收敛。与传统训练方法相比，δ = 0.2方法在相同的条件下收敛速度快9.58%。

相关工作

• Representation Learning

• Neural Networks

• Data driven approaches

方法

目前传统的小批量训练神经网络的方法由两个超参数定义，即epoch数E和批量大小B。epoch的数量E被定义为网络将通过整个数据集的总次数。批大小B是在每次迭代中传播到网络（小批）的样本数量。在训练网络的过程中，使用训练数据集DT，对学习网络的评估使用测试数据集Dt。在标准基准数据集上，假设DT和DT的分布是相似的。DT包含N个小批次，每个尺寸为B，Dt包含M个相同批次大小的小批次 B. 数据集表示为DT = {（xi，yi）} N i=0−1和Dt = {（xi，yi）} M i=0−1，其中x表示小批图像，y表示小批标签，两者的大小 B. 一次迭代对应于处理一个小批样本。

传统训练方法

小批量SGD的训练是训练神经网络最常见的方法。在小批SGD [5,24]中，对于每一个时代，总共有N个小批以N次迭代传播到网络中。具体来说，在每次迭代中，数据集DT的一个大小为B的小批被传递给网络进行反向传播。

损失函数L在每个小批量的转发传递过程中进行计算，然后对每个小批量进行反向传播。

工作流程如图2，左面板所示。在训练数据集的损失L被反向传播并更新权值N次后，得到的学习权值被用于在测试数据集Dt上验证网络。在测试阶段，网络的权值没有变化，只用于M个小批次的预测。训练指标和测试指标分别在M个和N个小批次上取平均值。

算法1中的反向传播的总数为（N×E），它等于迭代的次数和前向传递的次数。在概述中，传统的小批量训练方法更新权重N×E次，在等式1训练迭代的总数。

本文方法

提出的训练方法是通过一个新的超参数δ来学习整个数据集上的硬样本，该超参数δ代表了要考虑反向传播的小批量的比例。在该方法中，在DT中的N个小批次中，每次迭代中只有选择性地训练δ×N个小批次。由于δ∈(0,1]，（δ×N）≤N，∀N，该模型需要通过网络进行训练（E−1）/δ次，以确保网络对相同数量的权重更新进行训练。在一个时代内训练硬样本的次数被称为zeta (ζ)，如在等式中 2.具体步骤见算法2。

该网络首先在数据集中的N个小批上进行一次训练，形成一对小批bi及其相应的损失Li，即(bi ,Li)这些对存储在一个空间复杂度O (N)的列表中。这些对存储在一个空间复杂度O (N)的列表中。该列表可以表示为{（bi ，Li）} N i=0−1。这些对中的Li每反向传播重复ζ次更新，然后进行排序。对列表进行排序将导致平均时间复杂度为O（N×logN）。

N个小批次按损失Li的降序排列。排序的小批对的顺序称为（b‘i，Li），其中b’i是（δ×N）排序的选择进行训练的小批中的第i个小批。这些小批量的损失L被反向传播到网络中。这个过程重复了等式中的ζ次2和3。该方法每ζ次关注最难（δ×N）小批次。直观地说，该方法以每个数据集中的硬样本为目标，训练它们更多地更快地收敛。然而，传统的小批量训练方法并不关注数据集中代表不足的样本进行训练，这导致了更多的训练迭代次数。

实验

从表3可以看出，CIFAR-10上网络的性能取决于网络结构和训练中使用的δ的价值。一般来说，降低δ的值会导致更快的收敛速度和潜在的相似的泛化性能。

例如，在ResNet-18中，将δ从1.0降低到0.2，会导致收敛时间减少8.01%，但测试精度仅下降0.9%。然而，这一趋势在所有网络中都不一致，因为将δ从1.0降低到0.2实际上会导致EffificientNet netB4的测试精度的提高。值得注意的是，不同的网络架构具有不同的性能特征，这从不同网络之间的前1位测试精度和收敛时间的差异可以看出。例如，在所有的δ值中，效率NetB4具有最低的前1个测试精度，而ResNet-18对于δ = 1.0和0.8具有最高的前1个测试精度。总的来说，网络体系结构和δ价值的选择将取决于具体的应用和训练时间和泛化性能之间的权衡。

对于CIFAR-100，表4的结果表明，与传统的小批量训练相比，具有较小的δ值（0.2和0.5）的方法具有更好的测试top-1精度和更快的收敛速度。对于所有的网络，将δ值降低到0.2会导致更快的收敛时期。另一方面，更大的网络，如效率网和移动网，在收敛所需的时间上有了相当大的改进。与其他网络相比，移动网络网络似乎表现不佳。这可能是由于网络中的参数数量较少。

从表3、4、5中可以推断，在不同的数据集中，降低δ的值可以提高测试精度，提高大多数测试网络架构的收敛速度。与传统的小批量训练（δ = 1）相比，较小的δ值（0.2和0.5）通常会获得更好的测试精度和更快的收敛速度。但是，可以注意的是，δ的选择可能取决于小批次的总数，因为CIFAR-10和CIFAR-100比STL-10有更多的小批次。因此，δ = 0.2在CIFAR-10和CIFAR-100数据集中的收敛速度更快，而δ = 0.5在STL-10数据集中的收敛速度更快。此外，具有参数更多的大型网络在测试结果中比Mobilenet表现更好。因此，有必要根据网络架构来平衡模型选择、δ值和数据集，以达到最佳性能。

总结

总之，本研究提出了一种新的小批量训练方法，通过引入一种新的超参数δ，利用较小的批量规模。该方法为主要针对硬样本的神经网络训练提供了一种新的前景。该方法在CIFAR-10、CIFAR-100和STL-10数据集上进行了训练和验证。用于研究的网络有ResNet-18、ResNet-50、高效网络B4、高效NetV2-S和MobilenetV3-S。该方法可应用于任何神经网络训练，并可扩展到涉及反向传播的各种任务，以提高泛化和更快的收敛速度。我们的研究结果表明，δ值的选择应该仔细平衡网络架构、小批量数量和数据集的选择，以实现更快的收敛和相当可观的性能。

目前的方法的一些局限性可以概括如下：

这项工作为利用反向传播训练深度学习网络提供了一个新的视角。虽然在收敛方面有一些改进，但并不能保证模型能够提高性能。

该方法假设了样本的独立性，这在一些数据集中可能不成立，如在时间序列，三维图像，或视频。

该方法仅对分类任务进行了研究。

从局限性来看，未来的工作方向将集中在改进所提出的算法，扩展到包括依赖数据，并探索将该任务应用于其他任务，如目标检测、分割等。

该方法仅对分类任务进行了研究。

从局限性来看，未来的工作方向将集中在改进所提出的算法，扩展到包括依赖数据，并探索将该任务应用于其他任务，如目标检测、分割等。