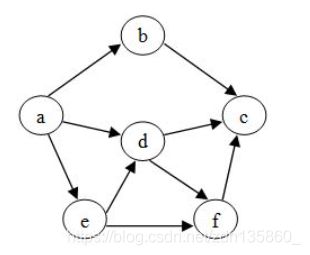
图2 2021-1-16

1-1
无向连通图至少有一个顶点的度为1。

F

1-2
用邻接表法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关。

F

1-3
在一个有向图中，所有顶点的入度与出度之和等于所有边之和的2倍。

T

1-4
如果无向图G必须进行两次广度优先搜索才能访问其所有顶点，则G中一定有回路。

F

1-5
用一维数组G[]存储有4个顶点的无向图如下：

G[] = { 0, 1, 0, 1, 1, 0, 0, 0, 1, 0 }
则顶点2和顶点0之间是有边的。

T

1-6
Prim 算法是维护一个森林，每一步把两棵树合并成一棵。

F

1-7
Kruskal 算法是维护一个森林，每一步把两棵树合并成一棵。

T

2-1
对于一个具有N个顶点的无向图，要连通所有顶点至少需要多少条边？
A.N−1
B.N
C.N+1
D.N/2

A

2-2
关于图的邻接矩阵，下列哪个结论是正确的？
A.有向图的邻接矩阵总是不对称的
B.有向图的邻接矩阵可以是对称的，也可以是不对称的
C.无向图的邻接矩阵总是不对称的
D.无向图的邻接矩阵可以是不对称的，也可以是对称的

B

2-3
图的深度优先遍历类似于二叉树的：
A.先序遍历
B.中序遍历
C.后序遍历
D.层次遍历

A

2-4
已知一个图的邻接矩阵如下，则从顶点V1出发按深度优先搜索法进行遍历，可能得到的一种顶点序列为：

A.V1,V2,V3,V4,V5,V6
B.V1,V2,V4,V5,V6,V3
C.V1,V3,V5,V2,V4,V6
D.V1,V3,V5,V6,V4,V2

B
题目有点问题

2-5
在图中自c点开始进行广度优先遍历算法可能得到的结果为：

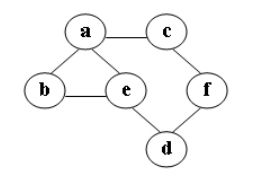
A.c,a,b,e,f,d
B.c,a,f,d,e,b
C.c,f,a,d,e,b
D.c,f,a,b,d,e

C

2-6
试利用 Dijkstra 算法求下图中从顶点 A 到其他顶点的最短距离及对应的路径。下列那个序列给出了可能的顶点收集顺序？

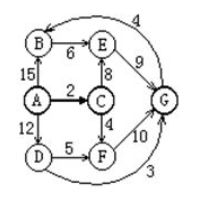
A.ACFEDBG
B.ACDBFEG
C。ACDGFBE
D.ABCDEFG

A

2-7
给定有向图如下。下列哪个选项不是对应的拓扑序列？

A.abedfc
B.aedbfc
C.aedfbc
D.abdfce

D