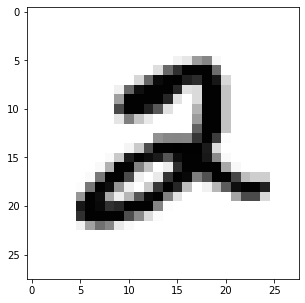从「降维打击」谈「降维」
生活中常常听到一个词:降维打击。
如何理解?
“王健林的小目标和我的小目标”就是最好的诠释。
对于数据来说,虽然不存在「打击」之说,但先对其降一波维,利用可视化的方式从整体上对数据有个事先的了解,再做后续分析,还是挺有用的,下面举两个例子。
示例1
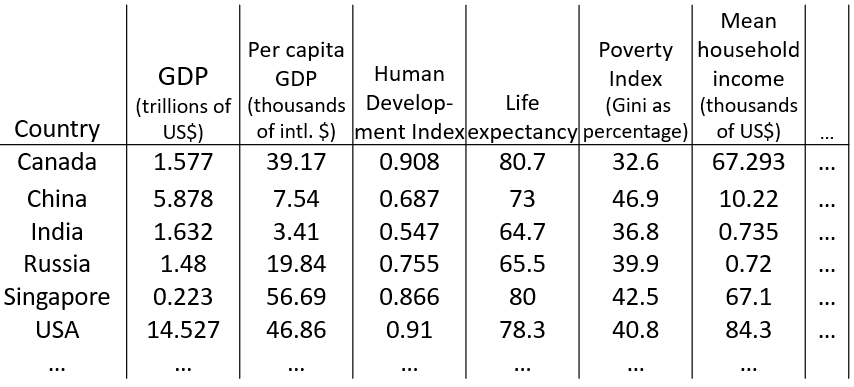
现有如下数据,每一行代表一个国家,每一列代表一个特征(比如GDP、居民生活指数等),那么该如何在建模前分析这些数据呢?
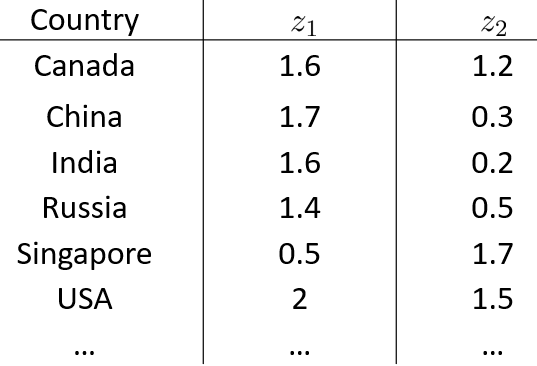
我们知道,对数据先进行可视化操作,能够在一开始就把握数据的整体情况。然而,在这个问题中不可能把每一个特征当做一个维度进行可视化,因为只要超过3维就难以进行绘图,这个时候,降维就有用了:通过特征转换,构造出两个特征z1、z2来概括这些特征,从而可以在二维坐标系里绘图(需要注意的是,我们需要弄清楚这两个特征大致是什么意思):
图一
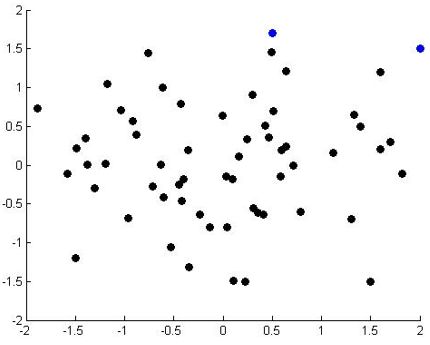
图二
假如图二中横坐标代表GDP,纵坐标代表人均GDP或个人经济活跃程度,那么可以看出,越靠右上的国家,GDP和个人经济活跃程度就越高,代表这个国家是比较发达的,同时个人的生活满意度也会比较高;越靠左下的国家,GDP和个人经济活跃程度就越低,可能是一些比较小的国家,同时居民的生活水平不会很高。
示例2
有时候拿到一些数据,但没有标签,从而不知道每个样本的属性是什么样的,那么,就需要利用诸如“聚类”的方法来初步探索数据,大概了解样本之间有没有什么共性。
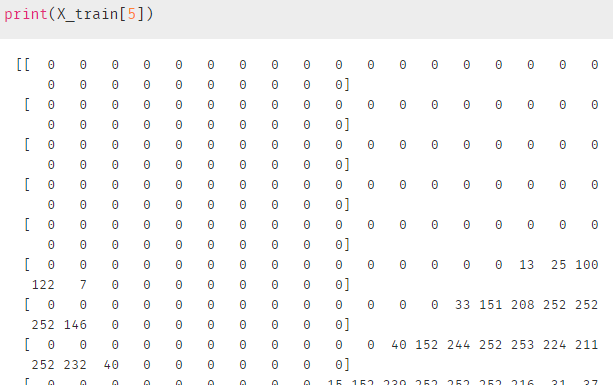
在计算机视觉领域,有一个入坑选手一定玩过的数据集——mnist手写数字数据集,随便选取一个样本,看看长什么样:
def image_show(image):
fig = plt.gcf()
fig.set_size_inches(5,5)
plt.imshow(image,cmap = 'binary')
plt.show()
image_show(X_train[5]) # 这里的5不是数字5,而是第6个样本输出:
上面是通过 .imshow( )函数可视化每个数字,如果直接输出这个样本,那么会得到一个长为784的向量:(更不可能通过这个来分析样本了)
下面看看如何通过降维,把784的维度降到2维,然后可视化这些样本:
# 导入要用到的库:
from keras.datasets import mnist
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.cluster import KMeans
from scipy.linalg import eigh
import seaborn as sns
#降维:
(X_train,Y_train),(X_test,Y_test) = mnist.load_data() # 加载数据
X = X_train[:10000] # 选取前10000个数据
X_train = X.reshape(10000,-1)
df = pd.DataFrame(X_train) # 生成数据框,更好看
s = StandardScaler() # 标准化
df1 = s.fit_transform(df)
cov = np.matmul(df1.T, df1) # 计算协差阵,cov.shape=(784, 784)
values, vectors = eigh(cov, eigvals = (782, 783)) # 计算特征值和特征向量
vectors = vectors.T # vectors.shape=(2, 784)
df2 = np.matmul(vectors, df1.T) # 和协差阵相乘,降维,df2.shape=(2, 10000)
final_dfT = np.vstack((df2, label)).T # 把标签加进去
dataFrame = pd.DataFrame(final_dfT, columns = ['pca_1', 'pca_2','label'])
# 绘图
g = sns.FacetGrid(dataFrame, hue = 'label',size=10)
g.map(sns.scatterplot, 'pca_1', 'pca_2')
g.add_legend()
plt.show()
最终:
由于上面是利用带标签的数据进行降维+可视化的,所以还少了点意思(真实情况可能没有标签,所以针对数据的先验知识是很有限的)。
下面就来看如何对没有标签的数据进行聚类+降维+可视化(尽管mnist中每个数字都带有标签,但我们假设所有数字是不带标签的):
# 数据依然用前面的:
X_train_1 = X.reshape(10000,784)
min_max_scaler = preprocessing.MinMaxScaler()
X_train_minmax = min_max_scaler.fit_transform(X_train_1) # 最大最小归一化
# 直接调用PCA函数进行降维,之前是手动降维
pca_1=PCA(n_components=2, copy = False)
X_reduce = pca_1.fit_transform(X_train_minmax) # X_reduce.shape=(10000, 2)
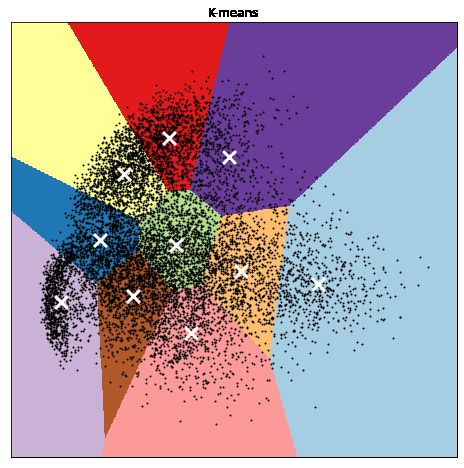
# 利用 k-means 聚类
reduced_data = X_reduce
kmeans = KMeans(n_clusters=10, n_init=4)
kmeans.fit(reduced_data)
# 绘图
h = 0.02
x_min, x_max = reduced_data[:, 0].min() - 1, reduced_data[:, 0].max() + 1
y_min, y_max = reduced_data[:, 1].min() - 1, reduced_data[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(figsize=(8,8))
plt.clf()
plt.imshow(
Z,
interpolation="nearest",
extent=(xx.min(), xx.max(), yy.min(), yy.max()),
cmap=plt.cm.Paired,
aspect="auto",
origin="lower",
)
plt.plot(reduced_data[:, 0], reduced_data[:, 1], "k.", markersize=2)
centroids = kmeans.cluster_centers_
plt.scatter(
centroids[:, 0],
centroids[:, 1],
marker="x",
s=169,
linewidths=3,
color="w",
zorder=10,
)
plt.title("K-means")
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show()最终:
可以看出,在没有标签的情况下,利用聚类算法可以把类间相似的样本聚到一块儿,然后降成可在平面上绘图的二维数据。
小结:在解决一个新问题时,拿到手的数据往往是比较杂乱的,如果能降到二维/三维,然后对这些数据进行可视化,那么会更有利于后续特征的选取、模型的选取等工作。
如有新的想法,期待交流探讨