高并发架构去重难?架构必备技能 - 布隆过滤器
系列文章目录
当Dubbo遇到高并发:探究流量控制解决方案
主从选举机制,架构高可用性的不二选择
高并发架构去重难?架构必备技能 - 布隆过滤器
- 系列文章目录
- 前言
- 一、布隆过滤器简介
- 二、特性与应用场景
- 三、参数定制
- 四、java版本的Demo
- 五、总结
前言
相信熟悉高并发架构的同学,一定都接触过一个名词————“布隆过滤器”,又或者一些朋友接触其实是在学习Redis的时候,了解到其中有这么一种数据类型。但实际上,除了Redis,在高并发或者各种存储性质的架构中,你经常能见到这种设计的存在,那么今天我们就好好说一说这个布隆过滤器
作者简介:战斧,从事金融IT行业,有着多年一线开发、架构及管理经验;爱好广泛,乐于分享,致力于创作更多高质量内容
本文收录于 JAVA架构,有需要者,可直接订阅专栏实时获取更新
高质量专栏 RabbitMQ、Spring全家桶 等仍在更新,欢迎指导
Zookeeper Redis kafka docker netty等诸多框架,以及架构与分布式专题即将上线,敬请期待
一、布隆过滤器简介
布隆过滤器是1970年由布隆(Burton Howard Bloom)提出的概率型数据结构:它通过位数组和哈希函数的巧妙结合它可以快速地判断一个元素是否属于某个集合,而且具有高效的存储和查询。虽然布隆过滤器是概率性的,但其性能却相当出色,尤其在处理大规模数据集时,能够显著减少资源消耗。
如下图:我们预先准备一块bit空间存放位数组,(所谓位数组就是一个数组,数组每个位置就是一个bit大小,只有0和1两种情况)。并定义两种哈希算法H1、H2。然后分别计算Orange 和 Lemon 这两个单词,显而易见的,我们将得到4个值,找到这4个值在bit空间的bit位,将其置为1。这就代表我们存入了Orange 和 Lemon 这两个单词。
必须清楚的一点是:布隆过滤器并不存储数据原文,只存数据经过哈希计算后的得到的位置,所以严格来说它能判重,但并不算容器。当下次再存Orange 或 Lemon的时候,执行上述步骤,我们就能发现对应bit位全为1,则代表数据可能存储过了
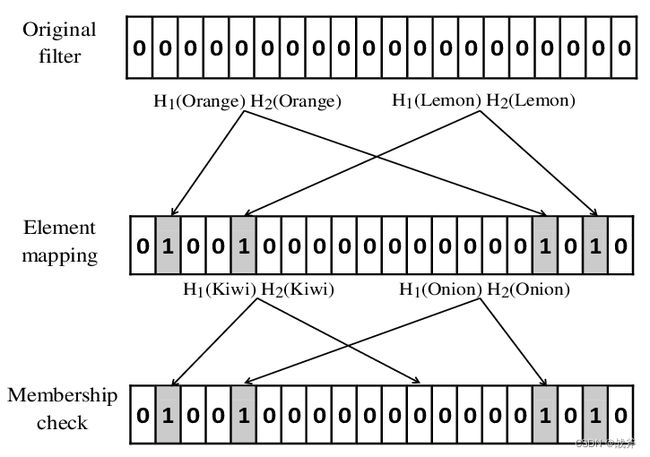
之所以说可能,是因为可能有别的单词,经过上述H1、H2计算后,落在同样的的两个bit位上,而恰好此时两个bit位都已经被置为1,从而导致误判(如上图的Onion单词)
二、特性与应用场景
其实从上面举得例子,不难总结出布隆过滤器至少有这么几个特性:
-
快速查询:布隆过滤器具有非常快速的查询操作。无论数据规模多大,查询的时间复杂度都是O(k),其中k是哈希函数的数量。
-
节省空间:相对于其他数据结构,布隆过滤器在存储大规模数据时非常节省空间。它使用位数组来存储数据,而不需要存储实际的元素本身。
-
概率性判断:布隆过滤器是一个概率性数据结构,意味着在判断一个元素是否存在时,有一定的误判率。如果判断元素不存在,那么它一定不存在;但如果判断元素存在,那么它可能并不存在,因为存在哈希冲突。
-
元素插入不可逆:一旦将元素插入布隆过滤器,就无法删除或修改该元素。因为删除元素需要将对应的位数组位置置为0,这可能会影响其他元素的判断。
-
哈希函数的重要性:布隆过滤器的性能和效果与使用的哈希函数密切相关。合理选择和设计哈希函数可以有效降低误判率。
结合上述特性,其实我们可以看到布隆过滤器 最适合的场景就是在大数据量下的判重, 因为其速度快、节约空间。虽然可能有“假阳性”(即不存在的数据也判重了)、bit位不可逆的问题,但这些问题通过哈希函数的选择,定好初始bit空间的大小,能很大的程度上的缓解。因此,至今,高并发或重存储的架构下,布隆过滤器,都有着广阔的应用。
三、参数定制
布隆过滤器的大小和哈希函数的个数是根据实际应用场景来确定的,需要平衡误判率和存储空间之间的关系。
一般来说,布隆过滤器的大小是根据预期要处理的数据量和误判率来确定的。误判率越小,需要的空间就越大。哈希函数的个数一般根据预期要处理的数据量和布隆过滤器的大小来确定,一般情况下,哈希函数的个数越多,误判率越小。
所以,使用布隆过滤器,有几个方面是我们一开始就要敲定的,就是对未来数据量的预估,以及误差率的限制。我们可以直接给出以下两个公式:
-
m = - (n * ln(p)) / (ln(2)^2) -
k = (m / n) * ln(2)
其中,m 表示布隆过滤器的大小,k 表示哈希函数的个数,n 表示要处理的数据量,p 表示允许的误差率。我们假设有如下场景:
我们要建立一个网盘产品,为避免一个文件重复存储,预计文件数量将达到20亿条数据,要求在用户上传文件时进行文件判重,误差率要求3%以内。
利用上面的公式:可以计算出:
m = - (20亿 * ln(0.03)) / (ln(2)^2) ≈ 14596881675.7 bits ≈ 1740 MB
k = ( 14596881675.7 / 20亿) * ln(2) ≈ 5.05
因此,可以将布隆过滤器的大小设置为 1740 MB,哈希函数的个数设置为 5个。
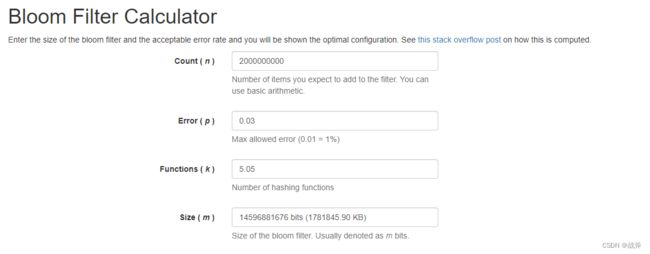
如果你懒得计算,这里也有一个现成的网站来帮你算: 布隆过滤器参数计算网站 ,可以看到结果是一致的。
四、java版本的Demo
我们可以利用JAVA中自带的hashCode函数,和BitSet类来写一个布隆过滤器的Demo
public class BloomFilter<T> {
private final int size;
private final BitSet bitSet;
public BloomFilter(int size) {
this.size = size;
this.bitSet = new BitSet(size);
}
private int hashFunction1(T value) {
return Math.abs(value.hashCode()) % size;
}
private int hashFunction2(T value) {
return Math.abs(value.hashCode() / 31) % size;
}
public void add(T value) {
int hash1 = hashFunction1(value);
int hash2 = hashFunction2(value);
bitSet.set(hash1);
bitSet.set(hash2);
}
public boolean contains(T value) {
int hash1 = hashFunction1(value);
int hash2 = hashFunction2(value);
return bitSet.get(hash1) && bitSet.get(hash2);
}
}
再写一个main函数进行验证,结果符合预期。
public static void main(String[] args) {
BloomFilter<String> bloomFilter = new BloomFilter<>(1000);
bloomFilter.add("apple");
bloomFilter.add("banana");
System.out.println(bloomFilter.contains("apple")); // Output: true
System.out.println(bloomFilter.contains("orange")); // Output: false
}
五、总结
虽然,我们在第四章使用java写出了一个布隆过滤器的Demo,但显然是不够好的,比如其设计容量得太小,还使用了两个关联的哈希函数。在真实环境中,如果要我们写过滤器,我们还是要严格遵守第三章的公式进行容量和哈希函数的计算。同时哈希函数也应该具有以下几个特点:
哈希函数需要快速计算,因为布隆过滤器的效率很大程度上依赖于哈希函数的效率哈希函数需要输出的哈希值应该尽可能分散、均匀,并且无法推断出输入元素的信息,这样可以使得误判率最小哈希函数互相之间应该独立,这样可以保证哈希值之间相互独立,降低误判率
当然,业界也有现成的布隆过滤器供我们使用,比如Google Guava BloomFilter 、Apache Commons Collections BloomFilter 还有很多人熟知的Redis BloomFilter。