重新审视MHA与Transformer
本文将基于PyTorch源码重新审视MultiheadAttention与Transformer。事实上,早在一年前博主就已经分别介绍了两者:各种注意力机制的PyTorch实现、从零开始手写一个Transformer,但当时的实现大部分是基于d2l教程的,这次将基于PyTorch源码重新实现一遍。
目录
- 1. MultiheadAttention
-
- 1.1 思路
- 1.2 源码
- 1.3 极简版MHA(面试用)
- 2. Transformer
- 3. Q&A
-
- 1. MHA的参数量?FLOPs?时间复杂度?
- 2. Transformer的总参数量?模型占用显存?
- 3. Transformer的FLOPs?
- 4. 参数量、FLOPs、时间复杂度汇总
- Ref
1. MultiheadAttention
1.1 思路
回顾多头注意力,其公式如下:
MHA ( Q , K , V ) = Concat ( head 1 , ⋯ , head h ) W O head i = Attn ( Q W i Q , K W i K , V W i V ) \text{MHA}(Q,K,V)=\text{Concat}(\text{head}_1,\cdots,\text{head}_h)W^O \\ \text{head}_i=\text{Attn}(QW_i^Q,KW_i^K,VW_i^V) MHA(Q,K,V)=Concat(head1,⋯,headh)WOheadi=Attn(QWiQ,KWiK,VWiV)
其中 W i Q ∈ R d m o d e l × d k W_i^Q\in \mathbb{R}^{d_{model}\times d_k} WiQ∈Rdmodel×dk, W i K ∈ R d m o d e l × d k W_i^K\in \mathbb{R}^{d_{model}\times d_k} WiK∈Rdmodel×dk, W i V ∈ R d m o d e l × d v W_i^V\in \mathbb{R}^{d_{model}\times d_v} WiV∈Rdmodel×dv, W O ∈ R h d v × d m o d e l W^O\in \mathbb{R}^{hd_v\times d_{model}} WO∈Rhdv×dmodel,且 d k = d v = d m o d e l / h d_k=d_v=d_{model}/h dk=dv=dmodel/h。
如果记 d h e a d = d m o d e l / h d_{head}=d_{model}/h dhead=dmodel/h,则 W i Q , W i K , W i V W_i^Q,W_i^K,W_i^V WiQ,WiK,WiV 的形状均为 ( d m o d e l , d h e a d ) (d_{model},d_{head}) (dmodel,dhead), W O W^O WO 的形状为 ( d m o d e l , d m o d e l ) (d_{model},d_{model}) (dmodel,dmodel)。
先不考虑batch和mask的情形,在只有一个头的情况下( h = 1 h=1 h=1),MHA的计算方式为
class MHA(nn.Module):
def __init__(self, d_model):
super().__init__()
self.w_q = nn.Parameter(torch.empty(d_model, d_model))
self.w_k = nn.Parameter(torch.empty(d_model, d_model))
self.w_v = nn.Parameter(torch.empty(d_model, d_model))
self.w_o = nn.Parameter(torch.empty(d_model, d_model))
self._reset_parameters()
def _reset_parameters(self):
for p in self.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
def forward(self, query, key, value):
"""
Args:
query: (n, d_model),n是query的个数,m是key-value的个数
key: (m, d_model)
value: (m, d_model)
"""
q = query @ self.w_q
k = key @ self.w_k
v = value @ self.w_v
attn_logits = q @ k.transpose(0, 1) / math.sqrt(q.size(1)) # attn_logits: (n, m)
attn_probs = F.softmax(attn_logits, dim=-1)
attn_output = attn_probs @ v # attn_output: (n, d_model)
return attn_output, attn_probs
现在考虑 h = 2 h=2 h=2 的情形,此时一共需要 3 ⋅ 2 + 1 = 7 3\cdot2+1=7 3⋅2+1=7 个参数矩阵
class MHA(nn.Module):
def __init__(self, d_model):
super().__init__()
self.w_q_1 = nn.Parameter(torch.empty(d_model, d_model // 2))
self.w_k_1 = nn.Parameter(torch.empty(d_model, d_model // 2))
self.w_v_1 = nn.Parameter(torch.empty(d_model, d_model // 2))
self.w_q_2 = nn.Parameter(torch.empty(d_model, d_model // 2))
self.w_k_2 = nn.Parameter(torch.empty(d_model, d_model // 2))
self.w_v_2 = nn.Parameter(torch.empty(d_model, d_model // 2))
self.w_o = nn.Parameter(torch.empty(d_model, d_model))
self._reset_parameters()
def _reset_parameters(self):
for p in self.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
def forward(self, query, key, value):
"""
Args:
query: (n, d_model),n是query的个数,m是key-value的个数
key: (m, d_model)
value: (m, d_model)
"""
q_1 = query @ self.w_q_1
k_1 = key @ self.w_k_1
v_1 = value @ self.w_v_1
q_2 = query @ self.w_q_2
k_2 = key @ self.w_k_2
v_2 = value @ self.w_v_2
attn_logits_1 = q_1 @ k_1.transpose(0, 1) / math.sqrt(q_1.size(1))
attn_probs_1 = F.softmax(attn_logits_1, dim=-1)
attn_output_1 = attn_probs_1 @ v_1
attn_logits_2 = q_2 @ k_2.transpose(0, 1) / math.sqrt(q_2.size(1))
attn_probs_2 = F.softmax(attn_logits_2, dim=-1)
attn_output_2 = attn_probs_2 @ v_2
attn_output = torch.cat([attn_output_1, attn_output_2], dim=-1) @ self.w_o # attn_output: (n, d_model)
attn_probs = torch.stack([attn_probs_1, attn_probs_2], dim=0) # attn_probs: (2, n, m),其中2是头数
return attn_output, attn_probs
可以看到代码量已经增加了不少,如果扩展到 h h h 个头的情形,则需要 3 h + 1 3h+1 3h+1 个参数矩阵。手动去一个个声明显然不现实,因为 h h h 是动态变化的,而用for循环创建又略显笨拙,有没有更简便的方法呢?
在上面的代码中,我们用小写 q q q 来代表查询 Q Q Q 经过投影后的结果( k , v k,v k,v 同理),即
q i = Q W i Q , i = 1 , 2 , ⋯ , h q_i=QW_i^Q,\quad i =1,2,\cdots,h qi=QWiQ,i=1,2,⋯,h
其中 Q Q Q 的形状为 ( n , d m o d e l ) (n,d_{model}) (n,dmodel), q i q_i qi 的形状为 ( n , d h e a d ) (n,d_{head}) (n,dhead),且有
h e a d i = softmax ( q i k i T d h e a d ) v i head_i=\text{softmax}\left(\frac{q_ik_i^{T}}{\sqrt{d_{head}}}\right)v_i headi=softmax(dheadqikiT)vi
注意到
[ q 1 , q 2 , ⋯ , q h ] = Q [ W 1 Q , W 2 Q , ⋯ , W h Q ] (1) [q_1,q_2,\cdots,q_h]=Q[W_1^Q,W_2^Q,\cdots,W_h^Q]\tag{1} [q1,q2,⋯,qh]=Q[W1Q,W2Q,⋯,WhQ](1)
如果记 q ≜ [ q 1 , q 2 , ⋯ , q h ] q\triangleq [q_1,q_2,\cdots,q_h] q≜[q1,q2,⋯,qh], W Q ≜ [ W 1 Q , W 2 Q , ⋯ , W h Q ] W^Q\triangleq [W_1^Q,W_2^Q,\cdots,W_h^Q] WQ≜[W1Q,W2Q,⋯,WhQ],则 W Q W^Q WQ 的形状为 ( d m o d e l , d m o d e l ) (d_{model},d_{model}) (dmodel,dmodel),与 h h h 无关, q q q 的形状为 ( n , d m o d e l ) (n,d_{model}) (n,dmodel)。这样一来,我们就不需要一个个声明 W i Q W_i^Q WiQ 了,并且可以一次性存储所有的 q i q_i qi。
要计算 h e a d 1 head_1 head1,我们需要能够从 q q q 中取出 q 1 q_1 q1( k , v k,v k,v 同理),所以我们期望 q q q 的形状是 ( h , n , d h e a d ) (h,n,d_{head}) (h,n,dhead),从而 q [ 1 ] q[1] q[1] 就是 q 1 q_1 q1(这里下标从 1 1 1 开始)。
当然也可以是 ( n , h , d h e a d ) (n,h,d_{head}) (n,h,dhead) 等形状,但必须要确保形状里含且只含这三个数字。之所以把 h h h 放在第一个维度是为了方便索引和后续计算。
同理可知 k , v k,v k,v 的形状均为 ( h , m , d h e a d ) (h,m,d_{head}) (h,m,dhead)。我们可以视 h h h 所在的维度为批量维,从而可以执行批量乘法 torch.bmm 来一次性算出 h h h 个头的结果。
q = torch.randn(h, n, d_head)
k = torch.randn(h, m, d_head)
v = torch.randn(h, m, d_head)
# @和torch.bmm的效果相同,但写法更简洁
attn_logits = q @ k.transpose(1, 2) / math.sqrt(q.size(2))
attn_probs = F.softmax(attn_logits, dim=-1)
attn_output = attn_probs @ v # attn_output: (h, n, d_head)
h h h 个头的结果存储在形状为 ( h , n , d h e a d ) (h,n,d_{head}) (h,n,dhead) 的张量中,那我们如何把这 h h h 个结果concat在一起呢?注意到我们实际上是将 h h h 个形状为 ( n , d h e a d ) (n,d_{head}) (n,dhead) 的张量横向concat为一个形状为 ( n , d m o d e l ) (n,d_{model}) (n,dmodel) 的张量,因此只需执行如下的形状变换:
( h , n , d h e a d ) → ( n , h , d h e a d ) → ( n , h ⋅ d h e a d ) = ( n , d m o d e l ) (2) (h,n,d_{head})\to(n,h,d_{head})\to(n,h\cdot d_{head})=(n,d_{model}) \tag{2} (h,n,dhead)→(n,h,dhead)→(n,h⋅dhead)=(n,dmodel)(2)
n = attn_output.size(1)
attn_output = attn_output.transpose(0, 1).reshape(n, -1)
⚠️ 注意,切勿直接将 ( h , n , d h e a d ) (h,n,d_{head}) (h,n,dhead) reshape成 ( n , d m o d e l ) (n,d_{model}) (n,dmodel)。
之前我们只讨论了 q q q 的形状应当是 ( h , n , d h e a d ) (h,n,d_{head}) (h,n,dhead),但并没有讨论它是如何变换得来的。这是因为, Q Q Q 在经过投影后得到的 q q q 只具有 ( n , d m o d e l ) (n,d_{model}) (n,dmodel) 的形状,要进行形状变换,一种做法是对 q q q 沿纵向切 h h h 刀再堆叠起来,这样从直观上来看也比较符合公式 ( 1 ) (1) (1)
q = torch.randn(n, d_model)
q = torch.stack(torch.split(q, d_head, dim=-1), dim=0)
但由于 W Q W^Q WQ 初始时是随机的,所以我们不需要严格按照公式 ( 1 ) (1) (1) 那样操作,直接执行 ( 2 ) (2) (2) 的逆变换即可
( n , d m o d e l ) = ( n , h ⋅ d h e a d ) → ( n , h , d h e a d ) → ( h , n , d h e a d ) (n,d_{model})=(n,h\cdot d_{head})\to(n,h,d_{head})\to(h,n,d_{head}) (n,dmodel)=(n,h⋅dhead)→(n,h,dhead)→(h,n,dhead)
现考虑有batch的情形,设批量大小为 b b b,则 Q Q Q 的形状为 ( b , n , d m o d e l ) (b,n,d_{model}) (b,n,dmodel) 或 ( n , b , d m o d e l ) (n,b,d_{model}) (n,b,dmodel),具体是哪一个要看 batch_first 是否为 True。接下来均假设 batch_first = False。
在以上的假设下, q q q 的形状也为 ( n , b , d m o d e l ) (n,b,d_{model}) (n,b,dmodel),我们将 b b b 和 h h h 看成同一维度(都是批量维),从而 ( 2 ) (2) (2) 式改写为
( n , b , d m o d e l ) → ( n , b , h , d h e a d ) → ( n , b ⋅ h , d h e a d ) → ( b ⋅ h , n , d h e a d ) (n,b,d_{model})\to(n,b,h,d_{head})\to(n,b\cdot h,d_{head})\to(b\cdot h,n,d_{head}) (n,b,dmodel)→(n,b,h,dhead)→(n,b⋅h,dhead)→(b⋅h,n,dhead)
关于 key_padding_mask 和 attn_mask 这里不再介绍,如有需要可阅读博主之前的文章,这里主要讲解如何合并两种mask。
前者的形状为 ( b , m ) (b,m) (b,m),用来mask掉key中的 [PAD],防止query注意到它。而后者的形状可以是 ( n , m ) (n,m) (n,m) 也可以是 ( b ⋅ h , n , m ) (b\cdot h,n,m) (b⋅h,n,m)。在实际合并两种mask的时候,我们均需要按照 ( b ⋅ h , n , m ) (b\cdot h,n,m) (b⋅h,n,m) 这个形状去计算。也就是说,如果是 key_padding_mask,我们需要进行形状变换 ( b , m ) → ( b , 1 , 1 , m ) → ( b , h , 1 , m ) → ( b ⋅ h , 1 , m ) (b,m)\to(b,1,1,m)\to(b,h,1,m)\to(b\cdot h,1,m) (b,m)→(b,1,1,m)→(b,h,1,m)→(b⋅h,1,m);如果是 attn_mask,我们需要进行形状变换 ( n , m ) → ( 1 , n , m ) (n,m)\to(1,n,m) (n,m)→(1,n,m)。
1.2 源码
本节将遵循以下记号:
| 记号 | 说明 |
|---|---|
| b b b | batch size |
| h h h | num heads |
| d d d | head dim |
| n n n | num queries |
| m m m | num key-value pairs |
首先实现一个MHA的基类:
class MultiheadAttentionBase_(nn.Module):
def __init__(self, embed_dim, num_heads, dropout=0., bias=True):
super().__init__()
self.embed_dim = embed_dim
self.num_heads = num_heads
self.dropout = dropout
self.head_dim = embed_dim // num_heads
assert self.head_dim * num_heads == embed_dim
self.in_proj_weight = nn.Parameter(torch.empty(3 * embed_dim, embed_dim))
if bias:
self.in_proj_bias = nn.Parameter(torch.empty(3 * embed_dim))
else:
self.register_parameter('in_proj_bias', None)
self.out_proj = nn.Linear(embed_dim, embed_dim, bias=bias)
self._reset_parameters()
def _reset_parameters(self):
nn.init.xavier_uniform_(self.in_proj_weight)
if self.in_proj_bias is not None:
nn.init.constant_(self.in_proj_bias, 0.)
nn.init.constant_(self.out_proj.bias, 0.)
def forward(
self,
query,
key,
value,
key_padding_mask,
attn_mask,
need_weights=True,
):
"""
Args:
query: (n, b, h * d)
key: (m, b, h * d)
value: (m, b, h * d)
key_padding_mask: (b, m), bool type
attn_mask: (n, m) or (b * h, n, m), bool type
Returns:
attn_output: (n, b, h * d)
attn_weights: (b, h, n, m)
"""
w_q, w_k, w_v = self.in_proj_weight.chunk(3)
if self.in_proj_bias is not None:
b_q, b_k, b_v = self.in_proj_bias.chunk(3)
else:
b_q = b_k = b_v = None
q = F.linear(query, w_q, b_q)
k = F.linear(key, w_k, b_k)
v = F.linear(value, w_v, b_v)
b, h, d = q.size(1), self.num_heads, self.head_dim
q, k, v = map(lambda x: x.reshape(-1, b, h, d), [q, k, v])
attn_mask = self.merge_masks(key_padding_mask, attn_mask, q)
attn_output, attn_weights = self.attention(q, k, v, attn_mask, out_proj=self.out_proj, dropout=self.dropout, training=self.training)
if not need_weights:
attn_weights = None
return attn_output, attn_weights
def merge_masks(self, key_padding_mask, attn_mask, q):
"""
Args:
key_padding_mask: (b, m), bool type
attn_mask: (n, m) or (b * h, n, m), bool type
q: only used to confirm the dtype of attn_mask
Returns:
attn_mask: (b * h, n, m), float type
"""
assert key_padding_mask is not None and key_padding_mask.dtype == torch.bool
b, m = key_padding_mask.size()
key_padding_mask = key_padding_mask.view(b, 1, 1, m).expand(-1, self.num_heads, -1, -1).reshape(b * self.num_heads, 1, m)
if attn_mask is not None:
assert attn_mask.dtype == torch.bool
if attn_mask.dim() == 2:
attn_mask = attn_mask.unsqueeze(0)
attn_mask = attn_mask.logical_or(key_padding_mask)
else:
attn_mask = key_padding_mask
attn_mask = torch.zeros_like(attn_mask, dtype=q.dtype).masked_fill_(attn_mask, -1e28)
return attn_mask
def attention(self, q, k, v, attn_mask, out_proj, dropout, training):
"""
Args:
q: (n, b, h, d)
k: (m, b, h, d)
v: (m, b, h, d)
attn_mask: (b * h, n, m), float type
out_proj: nn.Linear(h * d, h * d)
Returns:
attn_output: (n, b, h * d), is the result of concating h heads.
attn_weights: (b, h, n, m)
"""
raise NotImplementedError
接下来,只需要重写 attention 方法就可以实现普通版的MHA了
class MultiheadAttention(MultiheadAttentionBase_):
def attention(self, q, k, v, attn_mask, out_proj, dropout, training):
if not training:
dropout = 0
n, b, h, d = q.size()
q, k, v = map(lambda x: x.reshape(-1, b * h, d).transpose(0, 1), [q, k, v])
attn_logits = q @ k.transpose(-2, -1) / math.sqrt(d) + attn_mask
attn_probs = F.softmax(attn_logits, dim=-1)
attn_weights = F.dropout(attn_probs, p=dropout)
attn_output = attn_weights @ v
attn_output = attn_output.transpose(0, 1).reshape(n, b, h * d)
attn_output = out_proj(attn_output)
return attn_output, attn_weights
1.3 极简版MHA(面试用)
不少面试会让现场手写MHA,这里提供了一份模版,略去了很多细节。
相比原版,极简版做了如下改动:
- 略去了参数初始化。
- 去掉了mask
class MultiheadAttention(nn.Module):
def __init__(self, embed_dim, num_heads, dropout=0., bias=True):
super().__init__()
self.embed_dim = embed_dim
self.num_heads = num_heads
self.dropout = nn.Dropout(dropout)
self.head_dim = embed_dim // num_heads
assert self.head_dim * num_heads == embed_dim
self.in_proj_weight = nn.Parameter(torch.empty(3 * embed_dim, embed_dim))
if bias:
self.in_proj_bias = nn.Parameter(torch.empty(3 * embed_dim))
else:
self.register_parameter('in_proj_bias', None)
self.out_proj = nn.Linear(embed_dim, embed_dim, bias=bias)
def forward(self, query, key, value):
"""
Args:
query: (n, b, h * d)
key: (m, b, h * d)
value: (m, b, h * d)
"""
w_q, w_k, w_v = self.in_proj_weight.chunk(3)
if self.in_proj_bias is not None:
b_q, b_k, b_v = self.in_proj_bias.chunk(3)
else:
b_q = b_k = b_v = None
q, k, v = F.linear(query, w_q, b_q), F.linear(key, w_k, b_k), F.linear(value, w_v, b_v)
b, h, d = q.size(1), self.num_heads, self.head_dim
q, k, v = map(lambda x: x.reshape(-1, b * h, d).transpose(0, 1), [q, k, v])
attn_logits = q @ k.transpose(-2, -1) / math.sqrt(d)
attn_probs = F.softmax(attn_logits, dim=-1)
attn_weights = self.dropout(attn_probs)
attn_output = attn_weights @ v
attn_output = attn_output.transpose(0, 1).reshape(-1, b, h * d)
attn_output = self.out_proj(attn_output)
return attn_output, attn_weights
注意,如果尝试直接输出的话,会得到一堆 nan,这是因为没有xavier初始化,需要 _reset_parameters() 一下。
具体需要哪种mask可根据面试官的要求去实现。
2. Transformer
接下来基于PyTorch官方的MHA来实现Transformer。
首先需要实现一个基础函数,它可以用来复制一个 Module N次。
def _get_clones(module, n):
return nn.ModuleList([copy.deepcopy(module) for _ in range(n)])
EncoderLayer的实现
class TransformerEncoderLayer(nn.Module):
def __init__(
self,
d_model,
n_head,
d_ffn,
dropout=0.1,
activation=F.relu,
norm_first=False,
):
super().__init__()
self.self_attn = nn.MultiheadAttention(embed_dim=d_model, num_heads=n_head, dropout=dropout)
self.dropout1 = nn.Dropout(dropout)
self.linear1 = nn.Linear(d_model, d_ffn)
self.activation = activation
self.dropout2 = nn.Dropout(dropout)
self.linear2 = nn.Linear(d_ffn, d_model)
self.dropout3 = nn.Dropout(dropout)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.norm_first = norm_first
def forward(self, src, src_mask, src_key_padding_mask):
x = src
if self.norm_first:
x = x + self._sa_block(self.norm1(x), src_mask, src_key_padding_mask)
x = x + self._ff_block(self.norm2(x))
else:
x = self.norm1(x + self._sa_block(x, src_mask, src_key_padding_mask))
x = self.norm2(x + self._ff_block(x))
return x
def _sa_block(self, x, attn_mask, key_padding_mask):
x = self.self_attn(x, x, x, attn_mask=attn_mask, key_padding_mask=key_padding_mask, need_weights=False)[0]
return self.dropout1(x)
def _ff_block(self, x):
x = self.linear2(self.dropout2(self.activation(self.linear1(x))))
return self.dropout3(x)
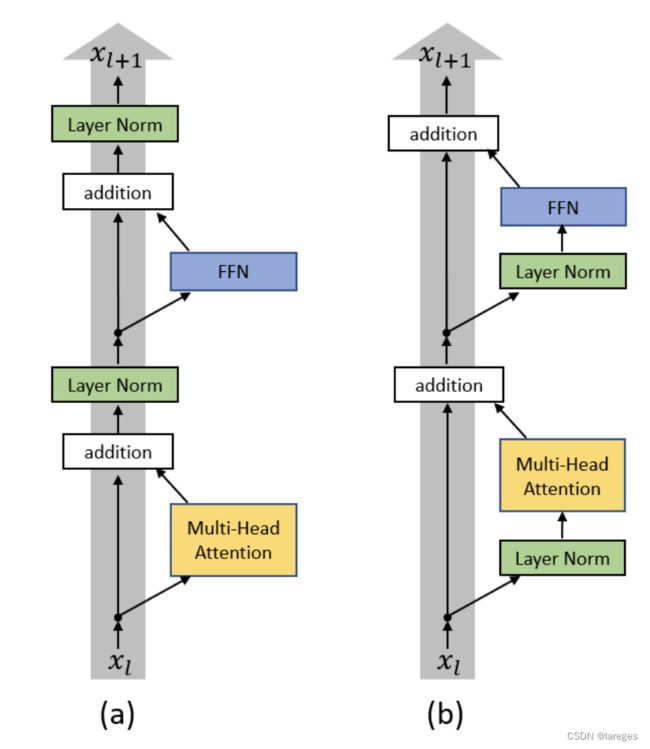
这里的 norm_first 用来决定是Pre-LN还是Post-LN,如下图所示
DecoderLayer的实现
class TransformerDecoderLayer(nn.Module):
def __init__(
self,
d_model,
n_head,
d_ffn,
dropout=0.1,
activation=F.relu,
norm_first=False,
):
super().__init__()
self.self_attn = nn.MultiheadAttention(embed_dim=d_model, num_heads=n_head, dropout=dropout)
self.dropout1 = nn.Dropout(dropout)
self.cross_attn = nn.MultiheadAttention(embed_dim=d_model, num_heads=n_head, dropout=dropout)
self.dropout2 = nn.Dropout(dropout)
self.linear1 = nn.Linear(d_model, d_ffn)
self.activation = activation
self.dropout3 = nn.Dropout(dropout)
self.linear2 = nn.Linear(d_ffn, d_model)
self.dropout4 = nn.Dropout(dropout)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.norm3 = nn.LayerNorm(d_model)
self.norm_first = norm_first
def forward(self, tgt, memory, tgt_mask, memory_mask, tgt_key_padding_mask, memory_key_padding_mask):
x = tgt
if self.norm_first:
x = x + self._sa_block(self.norm1(x), tgt_mask, tgt_key_padding_mask)
x = x + self._ca_block(self.norm2(x), memory, memory_mask, memory_key_padding_mask)
x = x + self._ff_block(self.norm3(x))
else:
x = self.norm1(x + self._sa_block(x, tgt_mask, tgt_key_padding_mask))
x = self.norm2(x + self._ca_block(x, memory, memory_mask, memory_key_padding_mask))
x = self.norm3(x + self._ff_block(x))
return x
def _sa_block(self, x, attn_mask, key_padding_mask):
x = self.self_attn(x, x, x, attn_mask=attn_mask, key_padding_mask=key_padding_mask, need_weights=False)[0]
return self.dropout1(x)
def _ca_block(self, x, mem, attn_mask, key_padding_mask):
x = self.cross_attn(x, mem, mem, attn_mask=attn_mask, key_padding_mask=key_padding_mask, need_weights=False)[0]
return self.dropout2(x)
def _ff_block(self, x):
x = self.linear2(self.dropout3(self.activation(self.linear1(x))))
return self.dropout4(x)
根据EncoderLayer搭建Encoder。需要注意的是,PyTorch源码中还提供了 encoder_norm 这一参数,即决定是否在Encoder最后放一个LN。
class TransformerEncoder(nn.Module):
def __init__(self, encoder_layer, num_layers, encoder_norm=None):
super().__init__()
self.layers = _get_clones(encoder_layer, num_layers)
self.num_layers = num_layers
self.encoder_norm = encoder_norm
def forward(self, src, src_mask, src_key_padding_mask):
output = src
for mod in self.layers:
output = mod(output, src_mask, src_key_padding_mask)
if self.encoder_norm is not None:
output = self.encoder_norm(output)
return output
DecoderLayer同理
class TransformerDecoder(nn.Module):
def __init__(self, decoder_layer, num_layers, decoder_norm=None):
super().__init__()
self.layers = _get_clones(decoder_layer, num_layers)
self.num_layers = num_layers
self.decoder_norm = decoder_norm
def forward(self, tgt, memory, tgt_mask, memory_mask, tgt_key_padding_mask, memory_key_padding_mask):
output = tgt
for mod in self.layers:
output = mod(output, memory, tgt_mask, memory_mask, tgt_key_padding_mask, memory_key_padding_mask)
if self.decoder_norm is not None:
output = self.decoder_norm(output)
return output
PyTorch官方的Transformer默认添加 encoder_norm 和 decoder_norm,然而这对于Post-LN的情形,无疑是多余的,所以这里我们做个简单修改,即如果是Post-LN情形,就不在最后添加LN了。
class Transformer(nn.Module):
def __init__(
self,
d_model=512,
n_head=8,
num_encoder_layers=6,
num_decoder_layers=6,
d_ffn=2048,
dropout=0.1,
activation=F.relu,
norm_first=False,
):
super().__init__()
if norm_first:
encoder_norm, decoder_norm = nn.LayerNorm(d_model), nn.LayerNorm(d_model)
else:
encoder_norm = decoder_norm = None
encoder_layer = TransformerEncoderLayer(d_model, n_head, d_ffn, dropout, activation, norm_first)
self.encoder = TransformerEncoder(encoder_layer, num_encoder_layers, encoder_norm)
decoder_layer = TransformerDecoderLayer(d_model, n_head, d_ffn, dropout, activation, norm_first)
self.decoder = TransformerDecoder(decoder_layer, num_decoder_layers, decoder_norm)
self._reset_parameters()
def _reset_parameters(self):
for p in self.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
def forward(
self,
src,
tgt,
src_mask=None,
tgt_mask=None,
memory_mask=None,
src_key_padding_mask=None,
tgt_key_padding_mask=None,
memory_key_padding_mask=None,
):
memory = self.encoder(src, src_mask, src_key_padding_mask)
output = self.decoder(tgt, memory, tgt_mask, memory_mask, tgt_key_padding_mask, memory_key_padding_mask)
return output
截止到目前,我们实现的Transfomer并不是完整的,还缺少embedding层和Decoder后面的Linear层,这里只介绍前者,因为后者仅仅是简单的 nn.Linear(d_model, tgt_vocab_size)。
Transformer的embedding层分为token embedding和Positional Encoding,前者是可学习的 nn.Embedding,后者是固定的Sinusoidal编码。
PE的公式为
P [ i , 2 j ] = sin ( i 1000 0 2 j / d m o d e l ) P [ i , 2 j + 1 ] = cos ( i 1000 0 2 j / d m o d e l ) 0 ≤ i < m a x _ l e n , 0 ≤ j < d m o d e l P[i,2j]=\sin\left(\frac{i}{10000^{2j/d_{model}}}\right)\\ P[i,2j+1]=\cos\left(\frac{i}{10000^{2j/d_{model}}}\right) \\ 0\leq i < max\_len,\;0\leq j
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout=0.1, max_len=5000):
super().__init__()
self.dropout = nn.Dropout(dropout)
position = torch.arange(max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) * (-math.log(10000.0) / d_model))
pe = torch.zeros(max_len, 1, d_model) # 1是batch size维度
pe[:, 0, 0::2] = torch.sin(position * div_term)
pe[:, 0, 1::2] = torch.cos(position * div_term)
self.register_buffer('pe', pe)
def forward(self, x):
x = x + self.pe[:x.size(0)]
return self.dropout(x)
3. Q&A
1. MHA的参数量?FLOPs?时间复杂度?
只考虑自注意力情形。为简便起见,令 h ≜ d m o d e l h\triangleq d_{model} h≜dmodel。
MHA模块一共包含四个参数矩阵: W Q , W K , W V , W O W^Q,W^K,W^V,W^O WQ,WK,WV,WO,形状均为 ( h , h ) (h,h) (h,h),因此weight部分的参数量是 4 ⋅ h 2 4\cdot h^2 4⋅h2。每个参数矩阵都会带有一个长度为 h h h 的bias,因此总共的参数量为 4 h 2 + 4 h 4h^2+4h 4h2+4h。
注意FLOPs和FLOPS的含义不同。前者是floating point operations,指浮点运算数,可以理解为计算量,用来衡量模型/算法的复杂度;后者是floating point operations per second,指每秒浮点运算次数,可以理解为计算速度,用来衡量衡量硬件的性能。
在计算形状为 ( m , n ) (m,n) (m,n) 和 ( n , k ) (n,k) (n,k) 矩阵的乘积时,每计算一次内积都要执行 n n n 次乘法和 n n n 次加法,而最终输出矩阵的形状为 ( m , k ) (m,k) (m,k),所以总共的浮点运算次数为 ( n + n ) ⋅ m ⋅ k = 2 m n k (n+n)\cdot m\cdot k=2mnk (n+n)⋅m⋅k=2mnk。
回到MHA,只考虑矩阵乘法:
- 首先会对形状为 ( l , b , h ) (l,b,h) (l,b,h) 的embedding进行投影,执行的矩阵乘法为 ( l , b , h ) × ( h , h ) → ( l , b , h ) (l,b,h)\times (h, h)\to(l,b,h) (l,b,h)×(h,h)→(l,b,h),这一步的计算量为 2 l b h 2 2lbh^2 2lbh2。由于会分别投影到 Q , K , V Q,K,V Q,K,V 三个矩阵,因此这一步的总计算量为 6 l b h 2 6lbh^2 6lbh2。
- 接下来是 Q K T QK^T QKT 相乘,执行的矩阵乘法为 ( b ⋅ n h , l , h d ) × ( b ⋅ n h , h d , l ) → ( b ⋅ n h , l , l ) (b\cdot nh,l,hd)\times(b\cdot nh,hd,l)\to(b\cdot nh,l,l) (b⋅nh,l,hd)×(b⋅nh,hd,l)→(b⋅nh,l,l),其中 n h nh nh 代表
num_heads, h d hd hd 代表head_dim。计算量为 2 l 2 b h 2l^2bh 2l2bh。 - 然后是对 V V V 进行加权,执行的矩阵乘法为 ( b ⋅ n h , l , l ) × ( b ⋅ n h , l , h d ) → ( b ⋅ n h , l , h d ) (b\cdot nh,l,l)\times(b\cdot nh,l,hd)\to(b\cdot nh,l,hd) (b⋅nh,l,l)×(b⋅nh,l,hd)→(b⋅nh,l,hd),计算量为 2 l 2 b h 2l^2bh 2l2bh。
- 最后的投影中,执行的矩阵乘法为 ( l , b , h ) × ( h , h ) → ( l , b , h ) (l,b,h)\times(h,h)\to(l,b,h) (l,b,h)×(h,h)→(l,b,h),计算量为 2 l b h 2 2lbh^2 2lbh2。
由上述步骤可知,MHA的FLOPs约为 6 l b h 2 + 2 l 2 b h + 2 l 2 b h + 2 l b h 2 = 4 l b h ( 2 h + l ) 6lbh^2+2l^2bh+2l^2bh+2lbh^2=4lbh(2h+l) 6lbh2+2l2bh+2l2bh+2lbh2=4lbh(2h+l)。
再来看MHA的复杂度,依然只考虑矩阵乘法。在计算形状为 ( m , n ) (m,n) (m,n) 和 ( n , k ) (n,k) (n,k) 矩阵的乘积时,计算内积的时间复杂度为 O ( n ) O(n) O(n),而输出矩阵的形状为 ( m , k ) (m,k) (m,k),填满这个矩阵所需要的时间为 O ( m k ) O(mk) O(mk),所以总时间复杂度为 O ( m n k ) O(mnk) O(mnk)。
可以发现一个不严谨的等式(仅针对矩阵乘法场景):
时间复杂度 = O ( FLOPs 2 ) 时间复杂度=O\left(\frac{\text{FLOPs}}{2}\right) 时间复杂度=O(2FLOPs)
由此可得到MHA的时间复杂度为 O ( 2 l b h ( 2 h + l ) ) = O ( l b h 2 + l 2 b h ) O(2lbh(2h+l))=O(lbh^2+l^2bh) O(2lbh(2h+l))=O(lbh2+l2bh)。特别地,当 b = 1 b=1 b=1 时,MHA的时间复杂度退化为 O ( l h 2 + l 2 h ) O(lh^2+l^2h) O(lh2+l2h)。
注意,MHA和SA(Self-Attention)的时间复杂度不同,SA的复杂度为 O ( l 2 h ) O(l^2h) O(l2h)。对于Restricted SA,注意力矩阵的每一行仅有 r r r 个元素需要计算,因此总共需要 r l rl rl 个元素需要计算,而计算每个元素的时间为 O ( h ) O(h) O(h),所以总时间为 O ( r l h ) O(rlh) O(rlh)。
2. Transformer的总参数量?模型占用显存?
此前已经计算出MHA部分的参数量为 4 h 2 + 4 h 4h^2+4h 4h2+4h,接下来看FFN部分。FFN有两个参数矩阵,形状分别为 ( h , 4 h ) (h,4h) (h,4h) 和 ( 4 h , h ) (4h,h) (4h,h),伴随它们的是两个bias,分别为 ( 4 h , ) (4h,) (4h,) 和 ( h , ) (h,) (h,),因此FFN部分的总参数量为 8 h 2 + 5 h 8h^2+5h 8h2+5h。
事实上,LayerNorm模块也有参数量,LN含有两个参数 γ \gamma γ 和 β \beta β,这两个参数均以形状为 ( h , ) (h,) (h,) 的张量进行存储,所以LN总共的参数为 2 h 2h 2h。
截至目前,我们可以做一个小总结:
| 模块 | 参数量 |
|---|---|
| MHA | 4 h 2 + 4 h 4h^2+4h 4h2+4h |
| FFN | 8 h 2 + 5 h 8h^2+5h 8h2+5h |
| LN | 2 h 2h 2h |
下面假设 num_encoder_layers 和 num_decoder_layers 均为 n n n。
一个EncoderLayer包含一个MHA,一个FFN和两个LN,所以一个EncoderLayer的参数量为 4 h 2 + 4 h + 8 h 2 + 5 h + 2 h ⋅ 2 = 12 h 2 + 13 h 4h^2+4h+8h^2+5h+2h\cdot 2=12h^2+13h 4h2+4h+8h2+5h+2h⋅2=12h2+13h,整个Encoder的参数量为 n ( 12 h 2 + 13 h ) n(12h^2+13h) n(12h2+13h)。
一个DecoderLayer包含两个MHA,一个FFN和三个LN,所以一个DecoderLayer的参数量为 8 h 2 + 8 h + 8 h 2 + 5 h + 6 h = 16 h 2 + 19 h 8h^2+8h+8h^2+5h+6h=16h^2+19h 8h2+8h+8h2+5h+6h=16h2+19h,整个Decoder的参数量为 n ( 16 h 2 + 19 h ) n(16h^2+19h) n(16h2+19h)。
由于PyTorch官方实现的Transformer还会默认增加 encoder_norm 和 decoder_norm,所以算上这两个LN,我们可以得到Transformer核心架构的参数量为 n ( 12 h 2 + 13 h ) + n ( 16 h 2 + 19 h ) + 2 h ⋅ 2 = n ( 28 h 2 + 32 h ) + 4 h n(12h^2+13h)+n(16h^2+19h)+2h\cdot 2=n(28h^2+32h)+4h n(12h2+13h)+n(16h2+19h)+2h⋅2=n(28h2+32h)+4h。将 n = 6 , h = 512 n=6,h=512 n=6,h=512 代入可得 6 ( 28 ⋅ 51 2 2 + 32 ⋅ 512 ) + 512 ⋅ 4 = 44140544 6(28\cdot 512^2+32\cdot 512)+512\cdot 4=44140544 6(28⋅5122+32⋅512)+512⋅4=44140544,该结果与下述代码的输出相同,这也验证了我们计算的正确性。
model = torch.nn.Transformer()
print(sum([p.numel() for p in model.parameters()]))
需要注意,上面提到了核心架构四个字,这是因为截至目前我们并没有计算出完整的Transformer的参数量。完整的Transformer除了核心架构外还应当包含Token Embedding和Decoder最后的线性层(即应当包含所有可学习的参数)。
假设Encoder和Decoder共用一个词表,且词表大小为 V V V,那么完整的Transformer的总参数量应当为
n ( 28 h 2 + 32 h ) + 4 h ⏟ 核心架构 + V ⋅ h ⏟ 词嵌入矩阵 + h ⋅ V ⏟ 输出层 = n ( 28 h 2 + 32 h ) + ( 4 + 2 V ) h \underbrace{n(28h^2+32h)+4h}_{核心架构}+\underbrace{V\cdot h}_{词嵌入矩阵}+\underbrace{h\cdot V}_{输出层}=n(28h^2+32h)+(4+2V)h 核心架构 n(28h2+32h)+4h+词嵌入矩阵 V⋅h+输出层 h⋅V=n(28h2+32h)+(4+2V)h
由于 V V V 要根据具体的数据集来确定,所以接下来我们只关心核心架构占用的显存。
PyTorch的Transformer的参数均以float32进行存储,一个浮点数占 4 4 4 个字节,那么核心架构总共占 44140544 ⋅ 4 / 102 4 2 ≈ 168 44140544\cdot4/1024^2\approx168 44140544⋅4/10242≈168 MB。由此可以看出,占用显存的大头其实还是数据,模型本身并不会占用太多。
3. Transformer的FLOPs?
此前已经得出MHA的FLOPs为 4 l b h ( 2 h + l ) 4lbh(2h+l) 4lbh(2h+l),接下来看FFN部分,我们依然只关心矩阵乘法。
显而易见,FFN部分会经历两次矩阵乘法:
- 第一次: ( l , b , h ) × ( h , 4 h ) → ( l , b , 4 h ) (l,b,h)\times(h,4h)\to(l,b,4h) (l,b,h)×(h,4h)→(l,b,4h),这一步的计算量为 8 l b h 2 8lbh^2 8lbh2;
- 第二次: ( l , b , 4 h ) × ( 4 h , h ) → ( l , b , h ) (l,b,4h)\times(4h,h)\to(l,b,h) (l,b,4h)×(4h,h)→(l,b,h),这一步的计算量为 8 l b h 2 8lbh^2 8lbh2;
LN部分不涉及矩阵乘法,Embedding部分仅仅是查表,也不涉及矩阵乘法,最后的输出层(计算logits)会涉及,即 ( l , b , h ) × ( h , V ) → ( l , b , V ) (l,b,h)\times(h,V)\to(l,b,V) (l,b,h)×(h,V)→(l,b,V),计算量 2 l b h V 2lbhV 2lbhV。
截至目前,我们可以做一个小总结:
| 模块 | FLOPs |
|---|---|
| MHA | 4 l b h ( 2 h + l ) 4lbh(2h+l) 4lbh(2h+l) |
| FFN | 16 l b h 2 16lbh^2 16lbh2 |
| Output | 2 l b h V 2lbhV 2lbhV |
由此可知,Encoder部分的FLOPs为 n ( 4 l b h ( 2 h + l ) + 16 l b h 2 ) = 4 n l b h ( 6 h + l ) n(4lbh(2h+l)+16lbh^2)=4nlbh(6h+l) n(4lbh(2h+l)+16lbh2)=4nlbh(6h+l),Decoder部分的FLOPs为 n ( 8 l b h ( 2 h + l ) + 16 l b h 2 ) = 8 n l b h ( 4 h + l ) n(8lbh(2h+l)+16lbh^2)=8nlbh(4h+l) n(8lbh(2h+l)+16lbh2)=8nlbh(4h+l),所以整个Transformer的FLOPs为
4 n l b h ( 6 h + l ) + 8 n l b h ( 4 h + l ) + 2 l b h V = 4 n l b h ( 14 h + 3 l ) + 2 l b h V 4nlbh(6h+l)+8nlbh(4h+l)+2lbhV=4nlbh(14h+3l)+2lbhV 4nlbh(6h+l)+8nlbh(4h+l)+2lbhV=4nlbh(14h+3l)+2lbhV
需要注意的是,虽然Embedding部分没有FLOPs,但仍可以计算它的时间复杂度。初始时,数据的形状为 ( b , l ) (b,l) (b,l),其中的每个元素都对应了token在vocab中的索引,通过该索引查表的时间复杂度为 O ( 1 ) O(1) O(1),因此嵌入过程 ( b , l ) → ( b , l , h ) (b,l)\to(b,l,h) (b,l)→(b,l,h) 的时间复杂度为 O ( l b ) O(lb) O(lb)。
同理可计算LN的时间复杂度。在对形状为 ( l , b , h ) (l,b,h) (l,b,h) 的张量进行LN时,LN会首先计算最后一个维度上的均值和方差,再对最后一个维度进行归一化处理,下面是一个简易版的LN
def layer_norm(x):
"""
Args:
x: (l, b, h)
"""
x_mean = torch.mean(x, dim=-1, keepdim=True)
x_std = torch.std(x, dim=-1, unbiased=False, keepdim=True) # 这里要使用有偏标准差
return (x - x_mean) / x_std
显然LN的时间复杂度为 O ( l b h ) O(lbh) O(lbh)。
4. 参数量、FLOPs、时间复杂度汇总
| 模块 | 参数量 | FLOPs(只考虑矩阵乘法) | 时间复杂度(不考虑批量) |
|---|---|---|---|
| MHA | 4 h 2 + 4 h 4h^2+4h 4h2+4h | 4 l b h ( 2 h + l ) 4lbh(2h+l) 4lbh(2h+l) | O ( l h 2 + l 2 h ) O(lh^2+l^2h) O(lh2+l2h) |
| FFN | 8 h 2 + 5 h 8h^2+5h 8h2+5h | 16 l b h 2 16lbh^2 16lbh2 | O ( l h 2 ) O(lh^2) O(lh2) |
| LN | 2 h 2h 2h | —— | O ( l h ) O(lh) O(lh) |
| Encoder | n ( 12 h 2 + 13 h ) n(12h^2+13h) n(12h2+13h) | 4 n l b h ( 6 h + l ) 4nlbh(6h+l) 4nlbh(6h+l) | O ( n ( l h 2 + l 2 h ) ) O(n(lh^2+l^2h)) O(n(lh2+l2h)) |
| Decoder | n ( 16 h 2 + 19 h ) n(16h^2+19h) n(16h2+19h) | 8 n l b h ( 4 h + l ) 8nlbh(4h+l) 8nlbh(4h+l) | O ( n ( l h 2 + l 2 h ) ) O(n(lh^2+l^2h)) O(n(lh2+l2h)) |
| Transformer-Core | n ( 28 h 2 + 32 h ) + 4 h n(28h^2+32h)+4h n(28h2+32h)+4h | 4 n l b h ( 14 h + 3 l ) 4nlbh(14h+3l) 4nlbh(14h+3l) | O ( n ( l h 2 + l 2 h ) ) O(n(lh^2+l^2h)) O(n(lh2+l2h)) |
| Embedding | V h Vh Vh | —— | O ( l ) O(l) O(l) |
| Output | V h Vh Vh | 2 l b h V 2lbhV 2lbhV | O ( l h V ) O(lhV) O(lhV) |
| Transformer-Complete | n ( 28 h 2 + 32 h ) + ( 4 + 2 V ) h n(28h^2+32h)+(4+2V)h n(28h2+32h)+(4+2V)h | 4 n l b h ( 14 h + 3 l ) + 2 l b h V 4nlbh(14h+3l)+2lbhV 4nlbh(14h+3l)+2lbhV | O ( n ( l h 2 + l 2 h ) + l h V ) O(n(lh^2+l^2h)+lhV) O(n(lh2+l2h)+lhV) |
据此,可以总结出:
- 参数量方面: FFN > MHA > LN,且单个FFN的参数量约为单个MHA的两倍。Decoder参数量略大于Encoder的参数量。 在整个Transformer中,FFN占 57.1 % 57.1\% 57.1%,MHA占 42.8 % 42.8\% 42.8%,LN占 0.1 % 0.1\% 0.1%。
- 耗时方面: MHA > FFN > LN,Transformer的计算主要都花在了MHA上。
- 计算量方面: 在整个Transformer的FLOPs中,当 h < 3 2 l h<\frac{3}{2}l h<23l 时,MHA的占比超过FFN,否则相反。
如有错误欢迎在评论区指出!
Ref
[1] https://zhuanlan.zhihu.com/p/264749298
[2] https://zhuanlan.zhihu.com/p/624740065