LeetCode每日一练 —— 88. 合并两个有序数组

前言

Wassup guys！我是Edison

今天是 LeetCode 上的 leetcode 88. 合并两个有序数组

Let’s get it！

---

---

1. 题目分析

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

示例 1：

示例 2：

示例 3：

2. 题目图解

非递减 的意思说明：不完全递增，数组后面的值不会比前面的值小。
 
并且当 nums1 和 nums2 合并以后，同样是 非递减顺序 的数组；
 
并且是把 nums2 合并到 nums1 中的，因为 num1 已经为 nums2 开好了的空间。

思路一

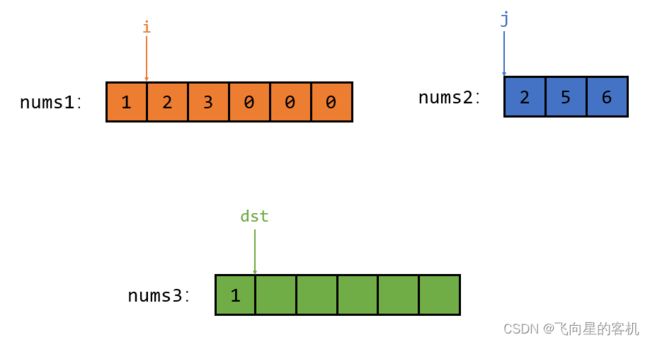
今天要介绍的第一种思路叫 归并，首先 nums1 和 nums2 数组如下

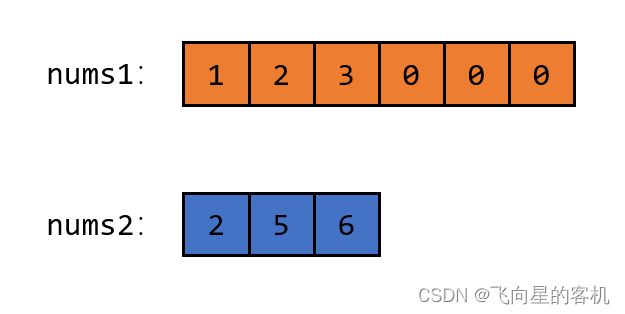
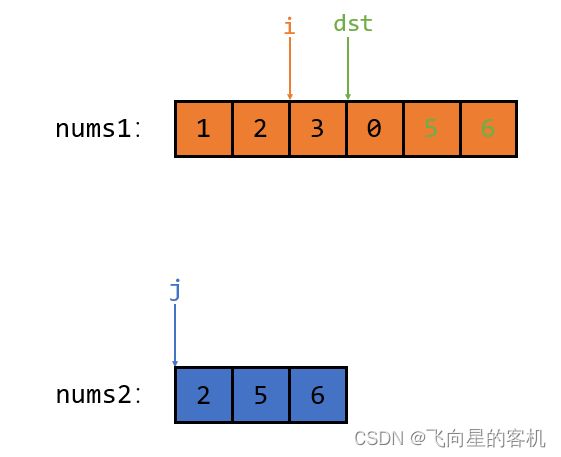
然后我们用 下标充当指针，指针 i 指向 nums1 的第一个元素，指针 j 指向 nums2 的第一个元素；

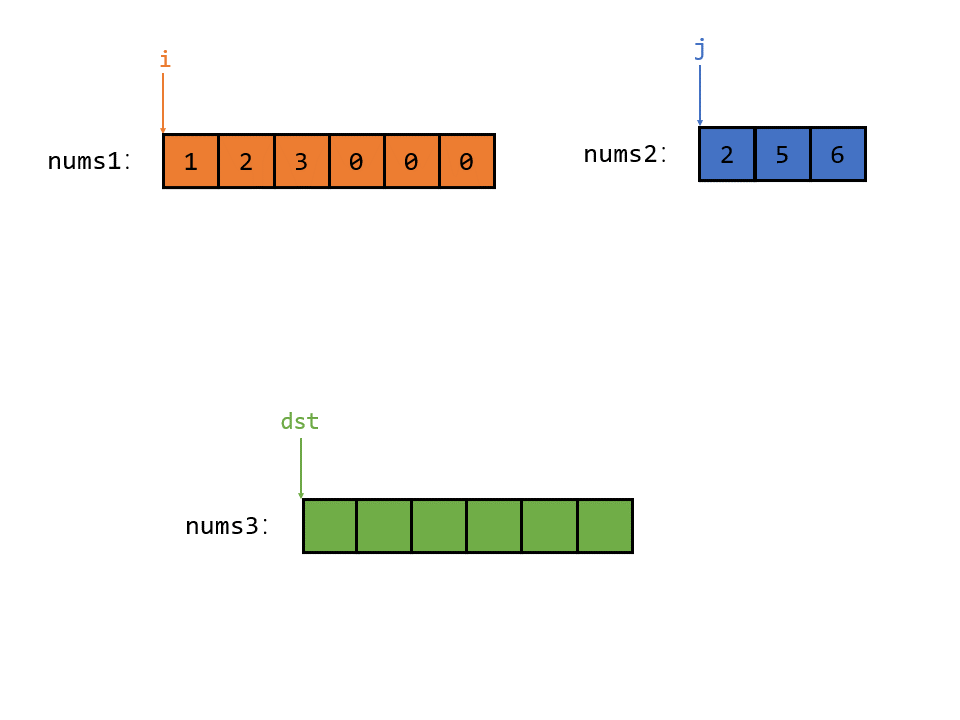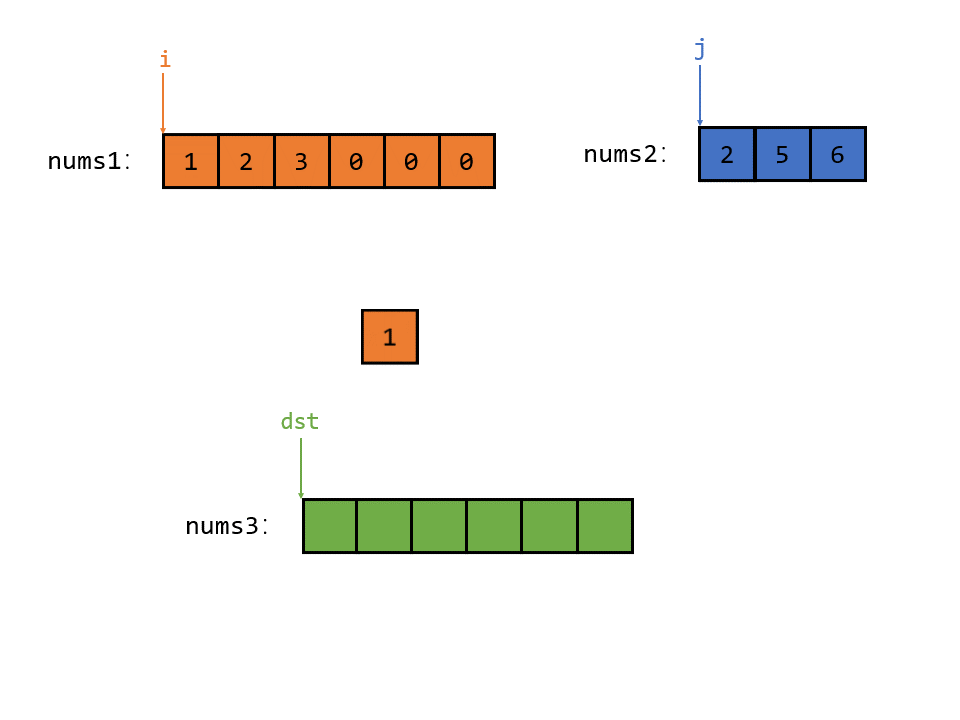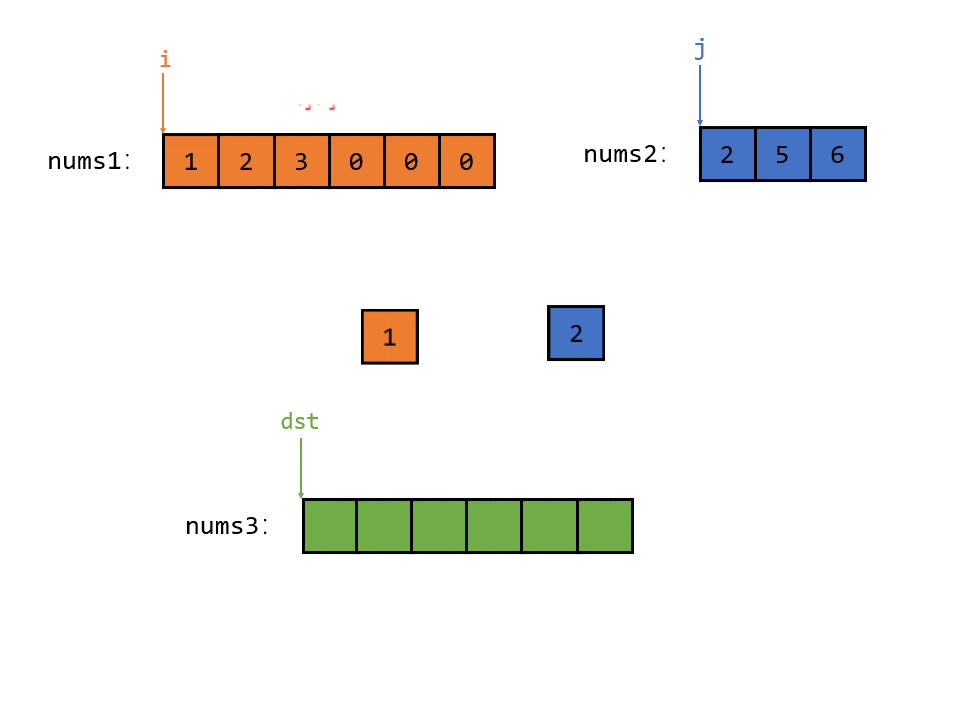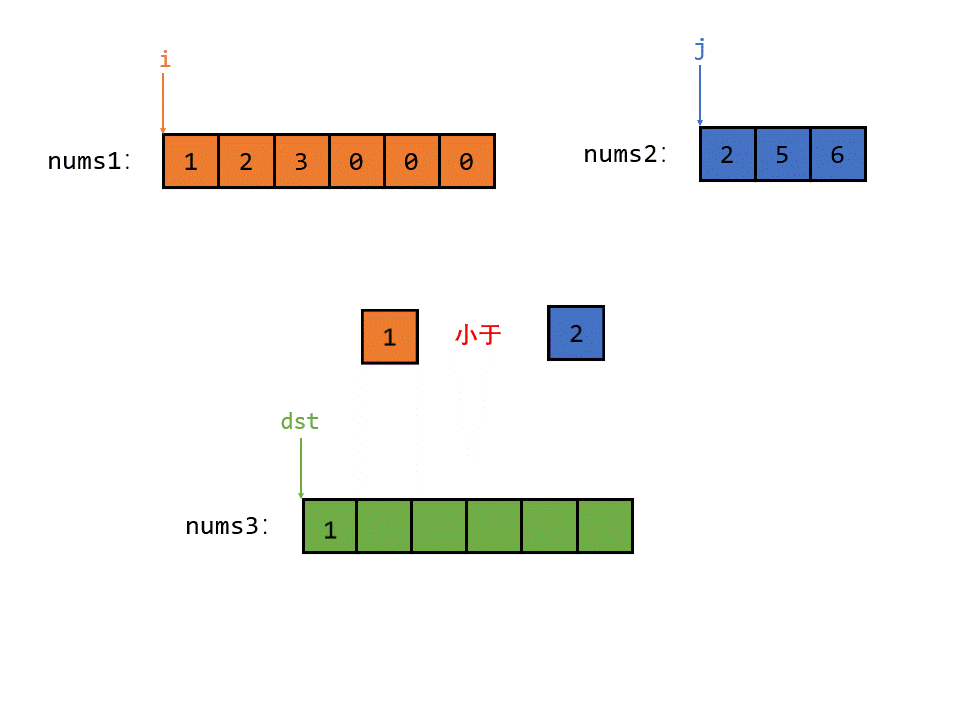
然后再开辟一个新的数组 nums3，并且 nums3 的大小和 nums1 一样，并且指针 dst 指向 nums3 的第一个元素；如图所示

首先 i 指向的元素小于 j 指向的元素，那么就把 i 指向的较小的元素放入 num3 中，如图所示

然后指针 i 和 dst 同时向后挪动

接着 i 与 j 指向的元素相等，那么随便把其中一个元素放入 nums3 中，假设把 j 放入 num3 中，如图所示

然后把指针 j 和 dst 同时向后挪动

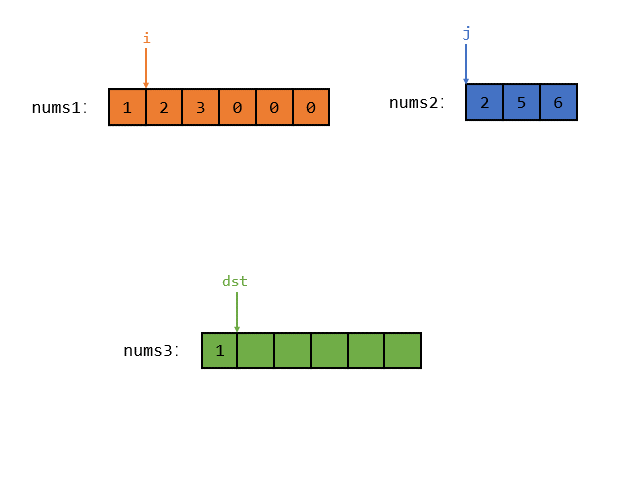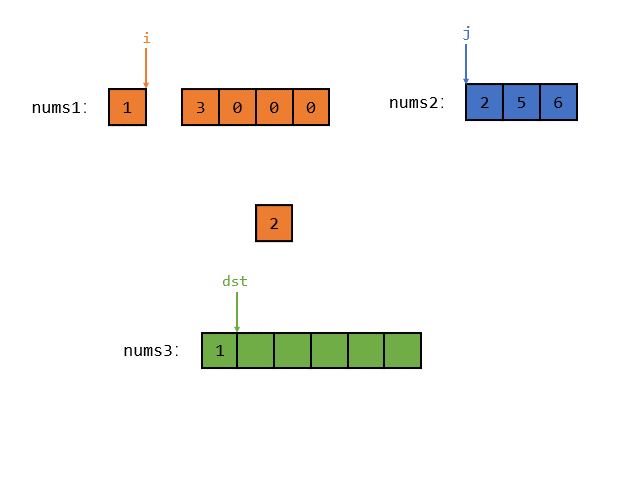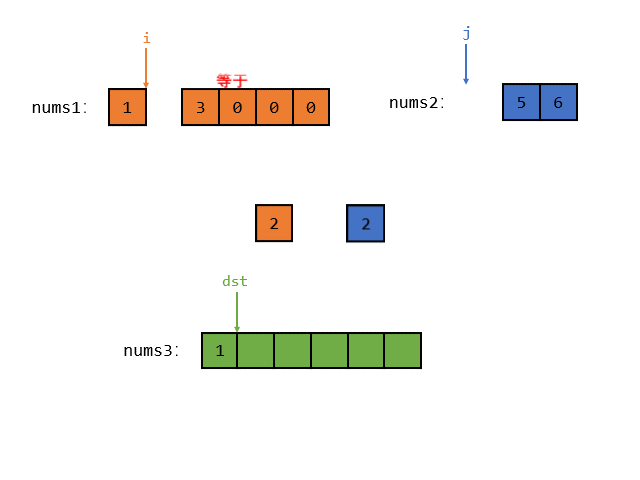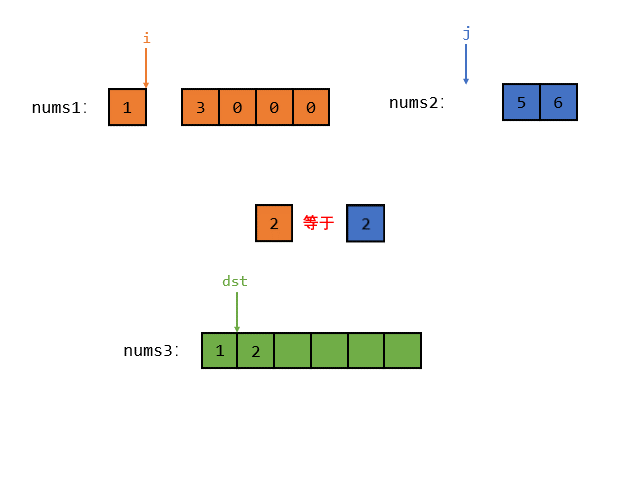
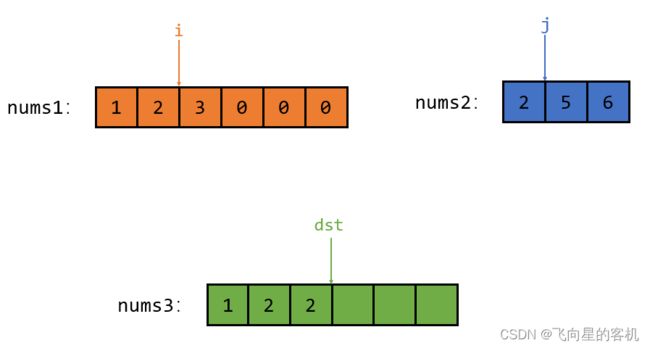
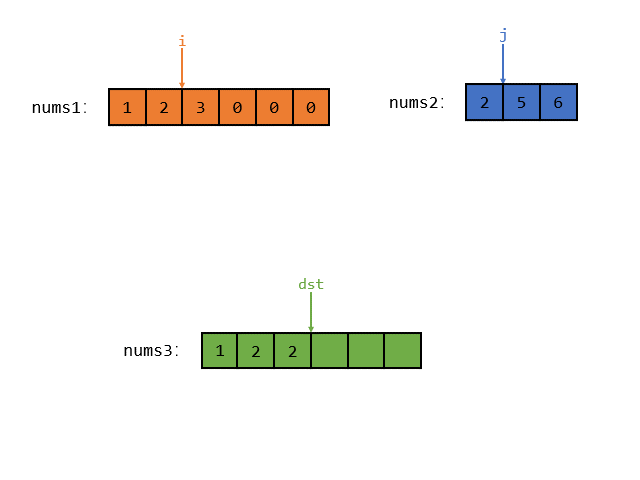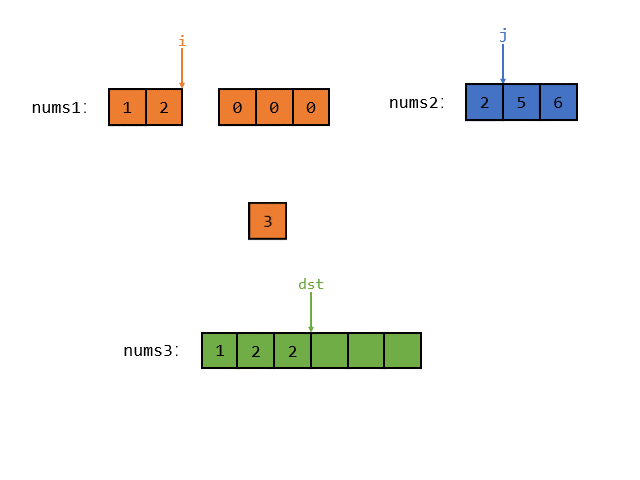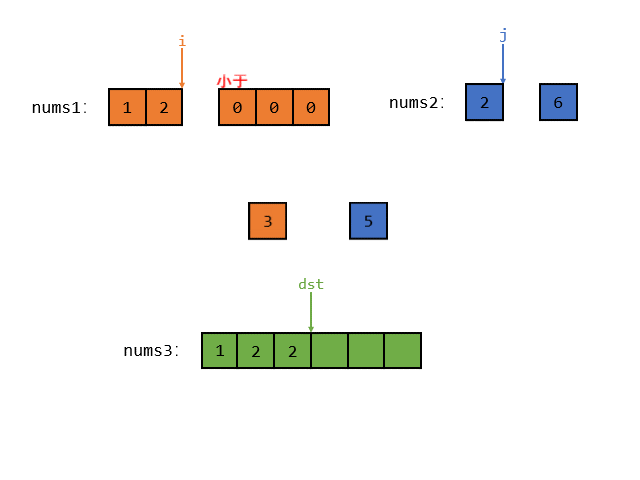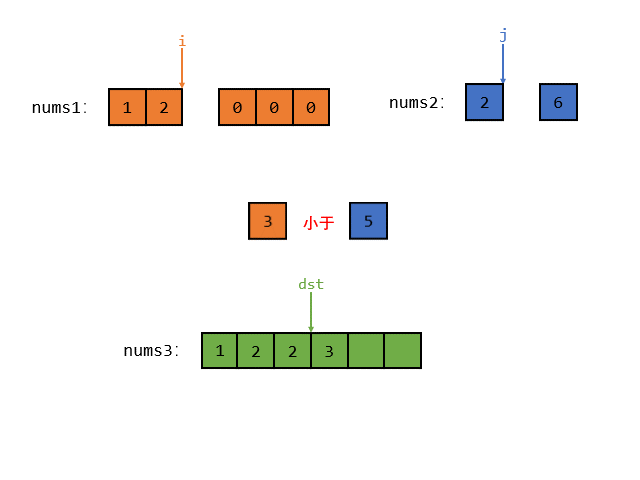
接着 i 指向的元素小于 j 指向的元素，那么就把 i 指向的较小的元素放入 num3 中，如图所示

然后指针 i 和 dst 同时向后挪动

接着 i 指向的元素还是小于 j 指向的元素，那么就把 i 指向的较小的元素放入 num3 中，如图所示

然后指针 i 和 dst 同时向后挪动

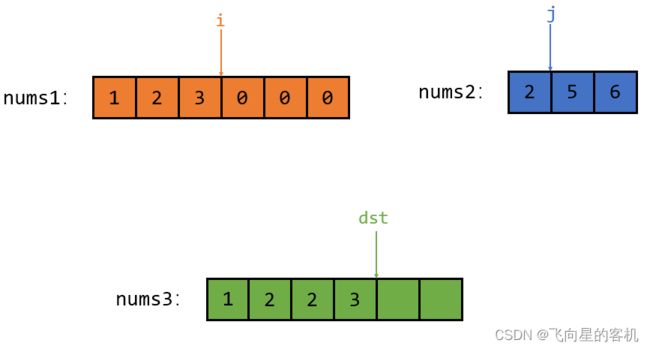
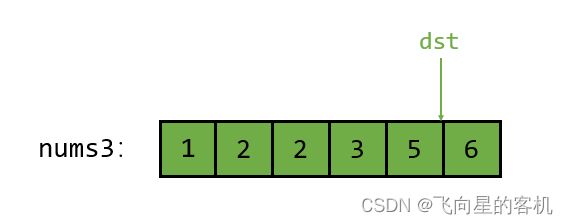
此时 nums1 中的元素已经走完了，那么直接把 nums2 中剩下的元素拿到 nums3 中去；

先把 j 指向的元素 5 拿过去，然后 j 和 dst 同时向后挪动

最后再把 j 指向的元素 6 拿过去

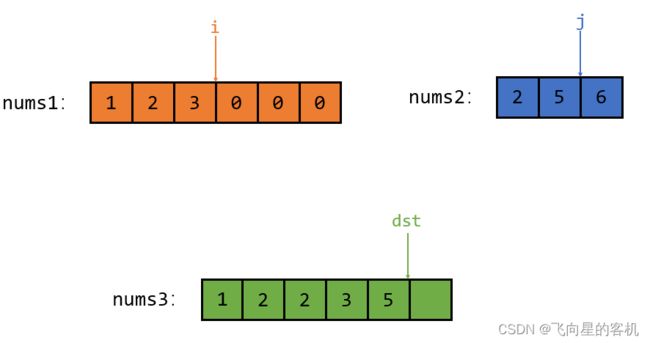
这种思路就是：依次比较，每次把小的放到归并数组中。

但是这种方法最大的问题在于：需要开一个额外的数组，那么就不符合题意要求了

思路二

思路一的方法是：从左向右依次遍历数组，取小的值；
 
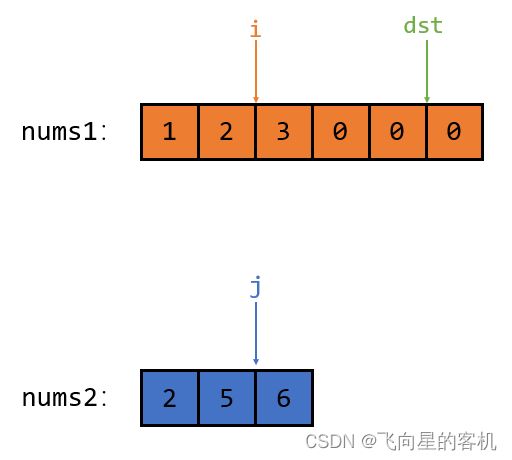
那么我可以选择 从右向左 取大的值，然后拿到 nums1 数组里面去，因为 nums1 数组已经开辟好了，有它俩合并到一起的空间；

还是用 下标充当指针，指针 i 指向 nums1 的最后一个 有效 元素，指针 j 指向 nums2 的最后一个 有效 元素；然后指针 dst 指向 nums1 的 最后一个空间的位置；

如图所示

首先 j 指向的元素大于 i 指向的元素，那么就把 j 指向的元素放入 dst 指向的位置中去，如图所示

然后指针 dst 和 j 同时向前挪动一位（谁指向的元素大，指针就减减）

接着 j 指向的元素还是大于 i 指向的元素，那么就把 j 指向的元素放入 dst 指向的位置中去，如图所示

然后指针 dst 和 j 同时向前挪动一位

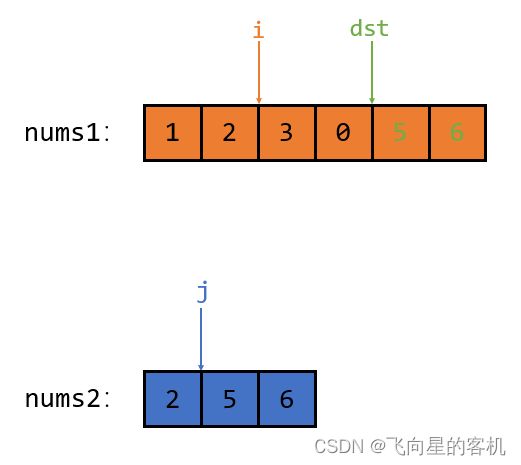
此时 i 指向的元素大于 j 指向的元素，那么就把 i 指向的元素放入 dst 指向的位置中去，如图所示

然后指针 dst 和 i 同时向前挪动一位

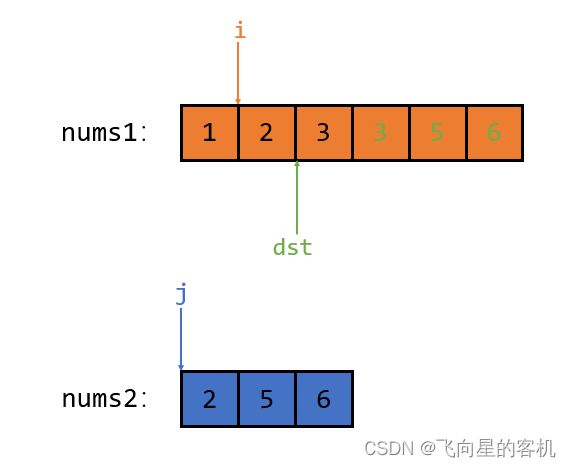
此时 i 指向的元素等于 j 指向的元素，那么就随便放一个元素到 dst 指向的位置中去；

假设就把 j 指向的元素放过去，然后指针 dst 和 j 同时向前挪动一位

可以看到此时指针 j 已经把 nums2 中的元素遍历完了，再往前走就形成 越界访问 了；

所以当 j 遍历完以后，就可以结束了；

但是还有下面这种情况

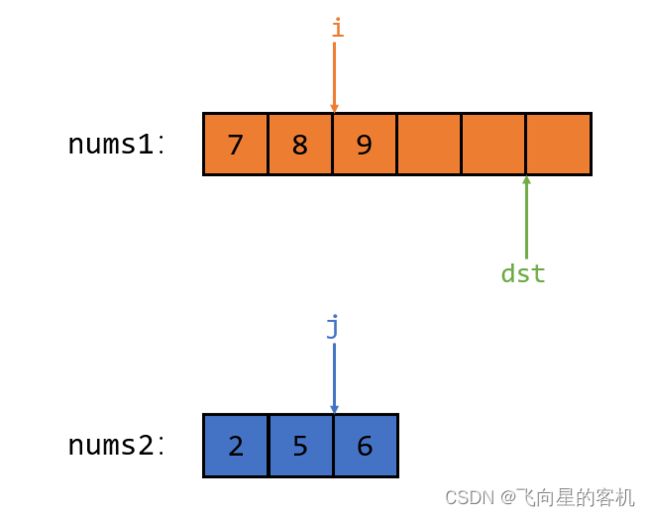
因为 nums1 数组中的值每一个都大于 nums2的，所以指针 i 肯定会提前把 nums1 遍历完，那么此时我们就需要把 num2 中的每一个元素都拿到 nums1 的前 3 个位置上去

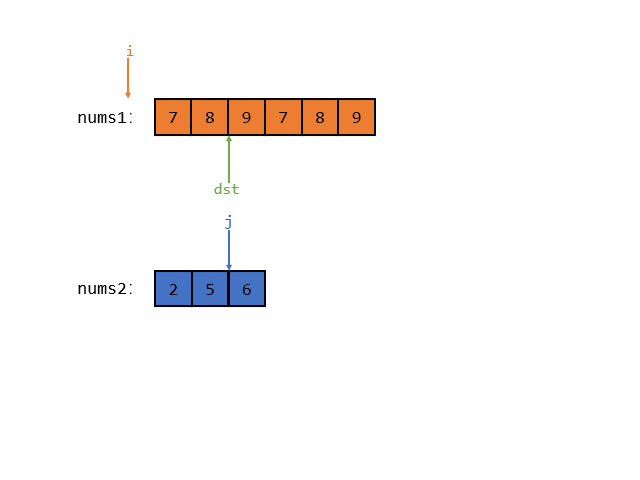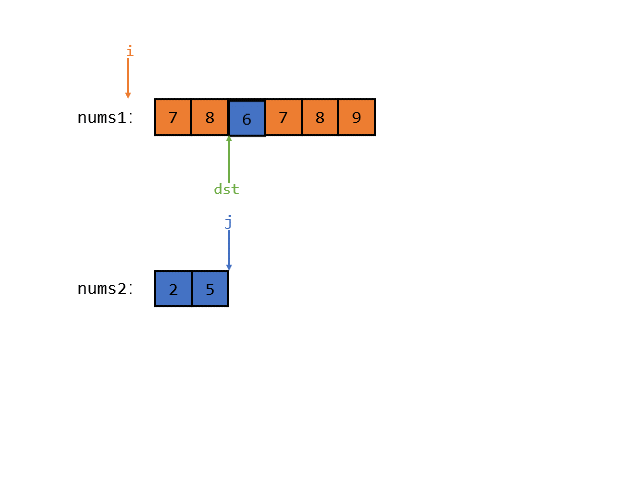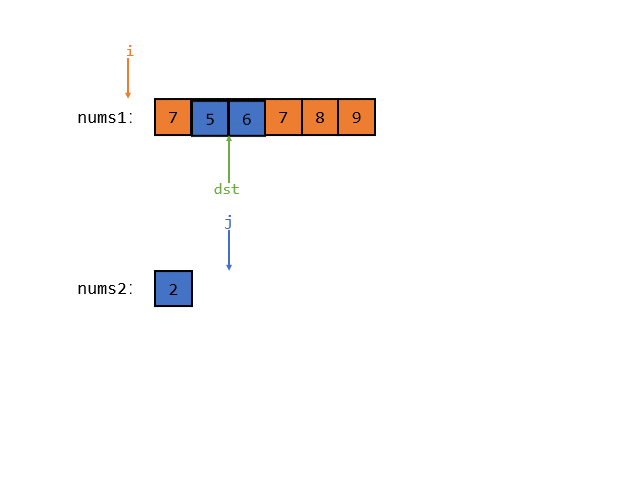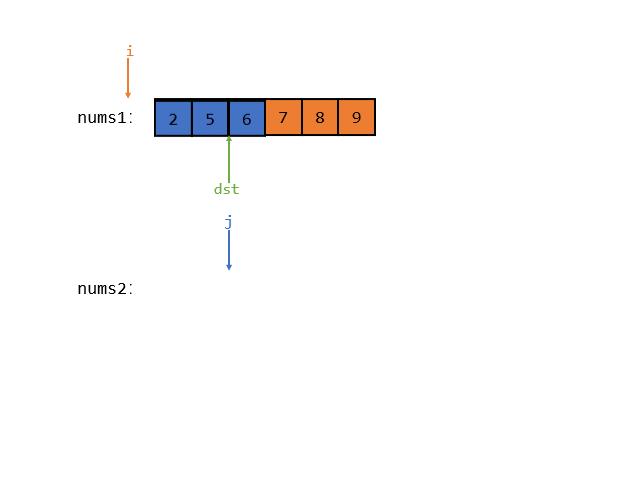
所以核心就是看哪个数组先遍历完！

这种方法没有开辟额外的空间，所以时间复杂度为 $O(M+N)$
 
m 为 nums 1 中的有效元素个数；
 
n 为 nums 2 中的有效元素个数。

3. 代码实现

接口代码

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){
    int i = m - 1;
    int j = n - 1;
    int dst = m + n - 1;
    // nums2 先走完的情况
    while (i >= 0 && j >= 0) {
        if (nums1[i] > nums2[j]) {
            nums1[dst] = nums1[i];
            --dst;
            --i;
        }
        else {
            nums1[dst] = nums2[j];
            --dst;
            --j;
        }
    }
    
    // nums1 先走完的情况
    while (j >= 0) {
        nums1[dst] = nums2[j];
        --dst;
        --j;
    }
}

其实还可以再简化一下

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){
    int i = m - 1;
    int j = n - 1;
    int dst = m + n - 1;
    // nums2 先走完的情况
    while (i >= 0 && j >= 0) {
        if (nums1[i] > nums2[j]) {
            nums1[dst--] = nums1[i--];
        }
        else {
            nums1[dst--] = nums2[j--];
        }
    }
    // nums1 先走完的情况
    while (j >= 0) {
        nums1[dst--] = nums2[j--];
    }
}

提交结果