二维背包问题（二维0-1背包）

问题描述

给定$n$种物品和一背包。物品$i$的重量是$w_i$，体积是$b_i$，其价值为$v_i$，背包的容量为$c$，容积为$d$。问应如何选择装入背包中的物品，使得装入背包中物品的总价值最大？在选择装入背包的物品是，对每种物品i只能有两种选择，即装入背包和不装入背包。不能将物品i装入背包多次，也不能只装入部分的物品$i$。尝试设计一个解决此问题的动态规划算法。

算法思路与代码实现

为了描述的方便（同时贴合我自己的代码），对一些表示符号稍作修改
物品i的重量表示为wi, 体积表示为bi，价值为vi
背包总容量为W，容积为B。（比较对应）

方法一：普通动归方法

从n个物品中的第n个物品开始考虑。设dp[i] [j] [k]是可选物品为i,i+1,…,n；背包容量为j，背包容积为k时的二维0-1背包问题的最优值（即最大价值数）

则状态转移方程如下：
$$dp[i][j][k]=\{\begin{array}{rlr}& max\{dp[i+1][j][k],dp[i+1][j-w_i][k-b_i]+v_i\}& j\ge w_i,0\le i\le n-1\\ & dp[i+1][j][k]& 0\le j<w_i,0\le i\le n-1\\ & v_n& j\ge w_n,i=n\\ & 0& 0\le j<w_n,i=n\end{array}$$

在该问题下，i∈[1,n]；j∈[0,W]；k∈[0,B]；最终问题转化为求dp[1] [W] [B]

至于得到具体背包内的物品，可以根据计算得出的dp[i] [j] [k]求出。具体做法是i从1到n变化，对比dp[i] [j] [k]和dp[i+1] [j] [k]的值，如果相同说明第i个物品没有被放入包中，让i=i+1继续做对比；如不相同则说明该物品放入包中，让j和k中的值减去第i个物品的重量和体积，再让i=i+1继续做对比，最终得到背包内装的所有物品。

从n个物品中的第1个物品开始考虑。设dp[i] [j] [k]是可选物品为1,2,…,i；背包容量为j，背包容积为k时的二维0-1背包问题的最优值（即最大价值数）

则状态转移方程如下：
$$dp[i][j][k]=\{\begin{array}{rlr}& max\{dp[i-1][j][k],dp[i-1][j-w_i][k-b_i]+v_i\}& j\ge w_i,1\le i\le n\\ & dp[i-1][j][k]& 0\le j<w_i,1\le i\le n\\ & v_1& j\ge w_1,i=1\\ & 0& 0\le j<w_1,i=1\end{array}$$

在该问题下，i∈[1,n]；j∈[0,W]；k∈[0,B]；最终问题转化为求dp[n] [W] [B]

如果我们让i=0表示没有可选物品，则可以进一步化简状态转移方程，变为如下形式：
$$dp[i][j][k]=\{\begin{array}{rlr}& max\{dp[i-1][j][k],dp[i-1][j-w_i][k-b_i]+v_i\}& j\ge w_i,0\le i\le n\\ & dp[i-1][j][k]& 0\le j<w_i,0\le i\le n\end{array}$$
显然，这样可以为后面的程序编写带来方便。

至于得到具体背包内的物品，可以根据计算得出的dp[i] [j] [k]求出。具体做法是i从n到0变化，对比dp[i] [j] [k]和dp[i-1] [j] [k]的值，如果相同说明第i个物品没有被放入包中，让i=i-1继续做对比；如不相同则说明该物品放入包中，让j和k中的值减去第i个物品的重量和体积，再让i=i-1继续做对比，最终得到背包内装的所有物品。

方法二：空间优化法

在上一种方法的基础上，容易发现每次的dp[i] [j] [k]只与dp[i-1] [j] [k]有关（或者dp[i+1] [j] [k]），这样只要每次重复利用上一轮的计算结果，就可以计算这次的dp[i] [j] [k]，也就可以通过循环控制去掉i这一维的空间，循环利用dp[j] [k]的二维空间。从而达到降低空间消耗的目的。

但这么做的会导致难以获取到背包最后具体装的物品。（因为每次计算的dp[i] [j] [k]被覆盖了）

代码1：方法一

从n个物品中的第1个物品开始考虑（从前往后考虑）。

#include
#include // standard_library
//  O(n*W*B) + O(n)
int max(int a,int b){
    if(a>b)return a;
    else return b;
} // 比较大小的函数
int main(){

	//声明参数和数据输入
	int n; // 物品个数
	printf("物品个数 n = "); scanf("%d",&n);
	int W; // 背包最大承受重量
	int B; // 背包最大容积
	int *w = (int*)malloc(sizeof(int)*(n+1)); // 记录物品重量,首位不用
	int *b = (int*)malloc(sizeof(int)*(n+1)); // 记录物品体积,首位不用
	int *v = (int*)malloc(sizeof(int)*(n+1)); // 记录物品价值,首位不用
	int *x = (int*)malloc(sizeof(int)*(n+1)); // 记录背包内存放了哪些物品。0表示没有放，1表示放了。首位不用。
	printf("背包最大承受重量 W = "); scanf("%d",&W);
	printf("背包最大容积 B = "); scanf("%d",&B);
	printf("每个物品的重量wi: ");for(int i=1;i<=n;i++)scanf("%d",&w[i]);
	printf("每个物品的体积bi: ");for(int i=1;i<=n;i++)scanf("%d",&b[i]);
	printf("每个物品的价值vi: ");for(int i=1;i<=n;i++)scanf("%d",&v[i]);

    // 动态规划找最优解 
    int i,j,k;
    	//声明并初始化dp[n+1][W+1][B+1]
    int ***dp = (int***)malloc(sizeof(int**)*(n+1));
	for(int i=0;i<=n;i++){
		dp[i] = (int**)malloc(sizeof(int*)*(W+1));
		for(int j=0;j<=W;j++){
			dp[i][j] = (int*)malloc(sizeof(int)*(B+1));
			for(int k=0;k<=B;k++)dp[i][j][k]=0; // 其内元素都置为零，这里同时也完成了第一行的初始化
		}
	}
    for(i=1;i<=n;i++){
        for(j=0;j<=W;j++){ //会出现j=w[i]的情况，所以遍历包含必须有j=0，下面k同理 
			for(k=0;k<=B;k++){
				if(j>=w[i] && k>=b[i]){
                	dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j-w[i]][k-b[i]]+v[i]);
            	}else{
               	 	dp[i][j][k] = dp[i-1][j][k];
           		}
			} 
        }
    }
		// 打印dp[n][W][B],即问题的最优值
    printf("maxValue = %d\n",dp[n][W][B]);

	// 计算x[i]，即分析最终背包内有哪些物品 
    for(i=n,j=W,k=B; i>0; i--){
    	if(dp[i][j][k]==dp[i-1][j][k]){ // 没有变化，说明没有选取 
    		x[i]=0;
		}else{
			x[i]=1; // 有变化，说明该物品被选取了  
			j -= w[i];
			k -= b[i];
		}
	}
	printf("x[i] = ");
	for(int i=1;i<=n;i++){
		printf("%d ",x[i]);
	}puts("");
	
return 0;
}

/* 一个测试用例如下
5
10
10
2 2 6 5 4
2 2 6 5 4
6 3 5 4 6

*/

从n个物品中的第n个物品开始考虑（从后往前考虑）。

#include
#include // standard_library
//  O(n*W*B) + O(n)
int max(int a,int b){
    if(a>b)return a;
    else return b;
}// 比较大小的函数
int main(){

	//声明参数和数据输入
	int n; // 物品个数
	printf("物品个数 n = "); scanf("%d",&n);
	int W; // 背包最大承受重量
	int B; // 背包最大容积
	int *w = (int*)malloc(sizeof(int)*(n+1)); // 记录物品重量,首位不用
	int *b = (int*)malloc(sizeof(int)*(n+1)); // 记录物品体积,首位不用
	int *v = (int*)malloc(sizeof(int)*(n+1)); // 记录物品价值,首位不用
	int *x = (int*)malloc(sizeof(int)*(n+1)); // 记录背包内存放了哪些物品。0表示没有放，1表示放了。首位不用。
	printf("背包最大承受重量 W = "); scanf("%d",&W);
	printf("背包最大容积 B = "); scanf("%d",&B);
	printf("每个物品的重量wi: ");for(int i=1;i<=n;i++)scanf("%d",&w[i]);
	printf("每个物品的体积bi: ");for(int i=1;i<=n;i++)scanf("%d",&b[i]);
	printf("每个物品的价值vi: ");for(int i=1;i<=n;i++)scanf("%d",&v[i]);

    // 动态规划找最优解 
    int i,j,k;
		//声明并初始化dp[n+1][W+1][B+1]
    int ***dp = (int***)malloc(sizeof(int**)*(n+1));
	for(int i=0;i<=n;i++){
		dp[i] = (int**)malloc(sizeof(int*)*(W+1));
		for(int j=0;j<=W;j++){
			dp[i][j] = (int*)malloc(sizeof(int)*(B+1));
			for(int k=0;k<=B;k++)dp[i][j][k]=0; // 其内元素都置为零
		}
	} 
		// 初始化i=n的情况
	for(j=0;j<=W;j++){
		for(k=0;k<=B;k++){
			if(j>=w[n] && k>=b[n]){
				dp[n][j][k] = v[n];
			}else {
				dp[n][j][k] = 0;
			}
		}
	}
    for(i=n-1;i>=1;i--){ // 从i=n-1 ... 1
        for(j=0;j<=W;j++){ // 会出现j=w[i]的情况，所以遍历包含必须有j=0，下面k同理 
			for(k=0;k<=B;k++){
				if(j>=w[i] && k>=b[i]){
                	dp[i][j][k] = max(dp[i+1][j][k], dp[i+1][j-w[i]][k-b[i]]+v[i]);
            	}else{
               	 	dp[i][j][k] = dp[i+1][j][k];
           		}
			} 
        }
    }
		// 打印dp[1][W][B],即问题的最优值
    printf("maxValue = %d\n",dp[1][W][B]); // 不是dp[n][W][B]
	
   	// 计算x[i]，即分析最终背包内有哪些物品 
    for(i=1,j=W,k=B; i<n; i++){ //由上到下
    	if(dp[i][j][k]==dp[i+1][j][k]){ // 没有变化，说明没有选取 
    		x[i]=0;
		}else{ // 有变化，说明该物品被选取了  
			x[i]=1; 
			j -= w[i];
			k -= b[i];
		}
	} // 以下考虑i=n情况
	x[n] = (dp[n][W][B])?1:0;
		// 打印x[i]
	printf("x[i] = ");
	for(int i=1;i<=n;i++){
		printf("%d ",x[i]);
	}puts("");
	
    
return 0;
}

代码2：空间优化法

#include
#include // standard_library
//  O(n*W*B) + O(n)

int max(int a,int b){
    if(a>b)return a;
    else return b;
}
int main(){
    
	//声明参数和数据输入
	int n; // 物品个数
	printf("物品个数 n = "); scanf("%d",&n);
	int W; // 背包最大承受重量
	int B; // 背包最大容积
	int *w = (int*)malloc(sizeof(int)*(n+1)); // 记录物品重量,首位不用
	int *b = (int*)malloc(sizeof(int)*(n+1)); // 记录物品体积,首位不用
	int *v = (int*)malloc(sizeof(int)*(n+1)); // 记录物品价值,首位不用
	int *x = (int*)malloc(sizeof(int)*(n+1)); // 记录背包内存放了哪些物品。0表示没有放，1表示放了。首位不用。
	printf("背包最大承受重量 W = "); scanf("%d",&W);
	printf("背包最大容积 B = "); scanf("%d",&B);
	printf("每个物品的重量wi: ");for(int i=1;i<=n;i++)scanf("%d",&w[i]);
	printf("每个物品的体积bi: ");for(int i=1;i<=n;i++)scanf("%d",&b[i]);
	printf("每个物品的价值vi: ");for(int i=1;i<=n;i++)scanf("%d",&v[i]);

    // 动态规划找最优解 
    int i,j,k;
    	//声明并初始化dp[n+1][W+1][B+1]
    int **dp = (int**)malloc(sizeof(int*)*(W+1));
	for(int i=0;i<=W;i++){
		dp[i] = (int*)malloc(sizeof(int)*(B+1));
		for(int j=0;j<=B;j++){
			dp[i][j]=0; // 其内元素都置为零
		}
	}
    for(i=1;i<=n;i++){
        for(j=W;j>=0;j--){ //会出现j=w[i]的情况，所以遍历包含必须有j=0，下面k同理 
			for(k=B;k>=0;k--){
				if(j>=w[i] && k>=b[i]){
                	dp[j][k] = max(dp[j][k], dp[j-w[i]][k-b[i]]+v[i]);
            	}else{
           		}
			} 
        }
    }

    printf("maxValue = %d\n",dp[W][B]);

    
return 0;
}

代码测试

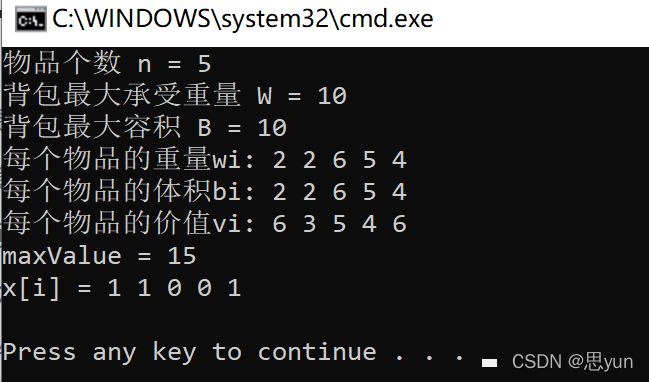
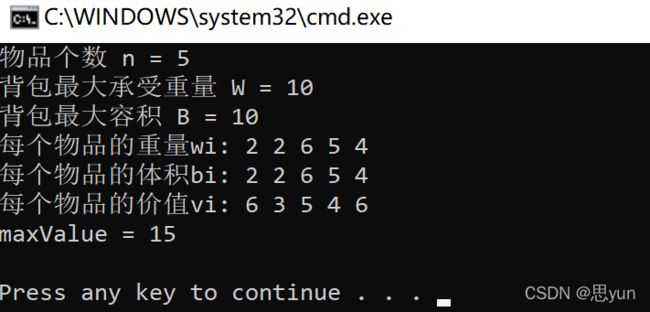
测试用例如下
n = 5; W = 10；B = 10;
wi = {2,2,6,5,4}; // 记录重量
bi = {2,2,6,5,4}; // 记录体积
vi = {6,3,5,4,6}; // 记录价值

方法一：

方法二：

算法心得和复杂度分析

算法复杂度分析:

对于以上的方法，求得最终结果dp[n] [W] [B]（或者dp[1] [W] [B]，或dp[W] [B]）,都经过了求其前面dp[][][] [] []的过程，所以算法复杂度来源于计算状态转移方程dp[i] [j] [k]的次数和计算一次状态转移方程的时间复杂度。计算次数受到物品个数，背包容量和容积的影响，为n*W*B次，而一次计算的时间复杂度显然是是常数级别的。

所以算法总的时间复杂度为O(n*W*B)，n为物品个数，W为背包容量（最大承受重量），B为背包容积。

空间复杂度分析：
在优化空间消耗前，需要使用三维数组，空间复杂度为O(n*W*B)，优化空间后降低为O(W*B)。

心得体会：
不同的选择考虑方式会有时会带来对编写程序方便。这个问题中，从n个物品中的第1个物品开始考虑（从前往后考虑），可以化简状态转移方程，让程序更加简单。

当每次一组数据的计算方法只依靠上一次的计算数据时，可以不开辟能够保存所有数据的空间大小，而是取每一次所序的空间大小，以此达到减少空间消耗的目的（滚动数组）。并且在算法设计时，必须防止要用于计算的数据被覆盖，在这个问题中体现的就是j必须逆向遍历。同时这么做也会导致计算过程中中间数据的丢失，难以获得到背包最后具体装的物品。

要想让程序能处理动态的数据，需要采用动态分配内存的方法声明dp数组

分享的同时记录学习，有问题欢迎交流指正。
觉得有用的话就点个赞吧！