逻辑推理与集合

逻辑推理与集合操作可以看做是同一个过程的不同展示方式，这两者具有不同的特点。

逻辑推理通常是一种思维过程、语言文本的形式。

而集合则很容易采用一种可视化的方式进行展示，并且集合很容易进行交集、并集、补集、差集等计算。

把语言的逻辑推理过程转换为集合操作，可以使得推理过程更加简单、更容易理解、更不容易出错。

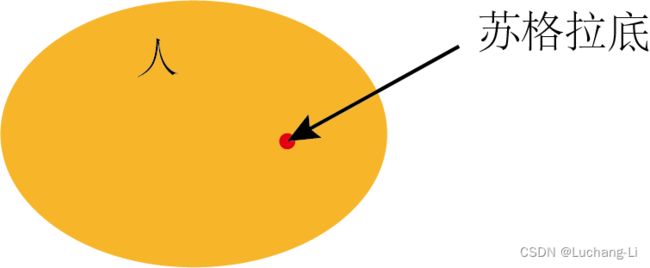
一个常见的三段论的逻辑推理例子：

人终有一死；
苏格拉底是人；
苏格拉底终有一死。

对应到集合操作可视化为下图

但是怎么根据集合操作得到或者检验最终的结论呢？

这只需要根据：

1. 集合整体成立的条件，其子集成员均成立。

2. 子集满足的特性其父/母集合中其他成员并不一定满足。

上面的例子中，因为苏格拉底是人的子集，因此人的集合整体满足的任何特性，作为人子集的苏格拉底都会满足。但是反过来就不成立：

苏格拉底是人;
苏格拉底终有一死;
人终有一死；

那么具体怎么把自然语言的逻辑推理转换为集合操作呢：

1. 把每个前提条件转换为相应的集合以及集合的交并补差等计算。

2. 得到结论所属的集合。

3. 把结论所属集合作为子集，检验其被包含的更大集合的性质得到该集合的性质。

充分、必要条件与集合

充分、必要条件定义参考： 

The Concept of Necessary Conditions and Sufficient Conditions

充分条件定义：

Definition: A condition A is said to be sufficient for a condition B, if (and only if) the truth (/existence /occurrence) [as the case may be] of A guarantees (or brings about) the truth (/existence /occurrence) of B.

如果A成立，那么B成立。

Definition: A condition A is said to be necessary for a condition B, if (and only if) the falsity (/nonexistence /non-occurrence) [as the case may be] of A guarantees (or brings about) the falsity (/nonexistence /non-occurrence) of B.

如果A不成立，则B不成立。

充分条件用集合来理解就是，因为A为B的子集，因此A满足B的特性，B所拥有的特性成立。

 

举两个例子，我们在中午或晚上会睡觉，那么如果中午可以推导出睡觉，晚上也可以推导出睡觉。

但是睡觉不能推导出中午。

a,b,c=3,4,5 -> a^2+b^2=c^2，但是a^2+b^2=c^2不能推出a,b,c=3,4,5

这里看上去跟第一部分内容是矛盾的，但实际上含义都是子集满足父集的特性。逻辑推理最重要的是找到结论所在的集合，以及所属的父集以及其成立的特性。

必要条件用集合理解是，因为父集的特性没有被满足，因此该成员不是子集成员。

例如：不睡觉->不是中午、晚上。a^2+b^2不等于c^2 -> a,b,c不等于3,4,5。

充分、必要条件与集合的关系简而言之：子集为充分条件，父集为必要条件，等集为充要条件。