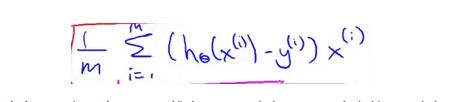多变量线性回归(二)
b站学习链接:传送门,学习视频第4、5章
学习目录索引:吴恩达2014课程简介
知识补充
思考一个问题:什么时候适合用线性回归?什么时候适合用多项式回归?
线性回归模型适合用于以下情况:
1. 数据具有线性关系:线性回归模型假设自变量和因变量之间存在线性关系,即当自变量发生变化时,因变量以线性方式相应变化。如果数据在散点图上呈现出明显的线性趋势,那么线性回归模型可能是一个合适的选择。
2. 数据的误差项满足正态分布和同方差性:线性回归模型假设误差项满足正态分布,并且具有相同的方差(同方差性)。这种假设在统计学中被称为线性回归模型的经典假设。如果数据的误差项满足这些假设,线性回归模型可以提供有效的参数估计和假设检验。
3. 特征之间具有较低的多重共线性:线性回归模型对于特征之间的多重共线性(高度相关性)是敏感的。多重共线性可能导致参数估计不准确或不稳定。因此,在应用线性回归模型之前,需要确保特征之间具有较低的共线性。
4. 预测变量与响应变量之间的关系可以通过线性函数进行很好地建模:如果预测变量与响应变量之间的关系可以很好地用线性函数进行近似,并且没有明显的非线性关系,线性回归模型可以提供一个简单且解释性强的模型。
需要注意的是,线性回归模型是一种简单但常用的回归方法。对于复杂的数据和非线性关系,线性回归可能无法提供准确的预测。在这种情况下,可能需要考虑其他更复杂的模型或采用非线性回归技术。
多项式回归适合用于以下情况:
1. 数据具有非线性关系:当数据在散点图上显示出明显的非线性趋势时,多项式回归可以提供更灵活的建模能力。通过引入多项式特征,可以捕捉到数据中的非线性关系,从而更好地拟合数据。
2. 预测变量与响应变量之间的关系可以通过多项式函数进行近似:多项式回归将预测变量的多项式项作为特征,使模型能够更好地拟合数据。如果预测变量与响应变量之间的关系可以用多项式函数进行近似,并且存在高阶项的影响,那么多项式回归可以提供更准确的建模。
3. 存在交互项和非线性效应:多项式回归还可以捕捉到特征之间的交互作用和非线性效应。通过引入交互项和高阶项,可以捕捉到特征之间的相互作用和非线性效应,从而更全面地描述数据。
需要注意的是,多项式回归可以在一定程度上增加模型的复杂性,特别是在引入高阶项时。过度复杂的模型可能会导致过拟合问题,因此在应用多项式回归之前,需要仔细考虑模型的复杂性和数据的规模。此外,当数据量较少时,高阶多项式回归可能会过度拟合数据,因此需要谨慎选择多项式的阶数。
课堂笔记
多维特征
参考视频: 4 - 1 - Multiple Features (8 min).mkv
目前为止,我们探讨了单变量/特征的回归模型,现在我们对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为 ( x 1 , x 2 , . . . , x n ) \left( {x_{1}},{x_{2}},...,{x_{n}} \right) (x1,x2,...,xn)。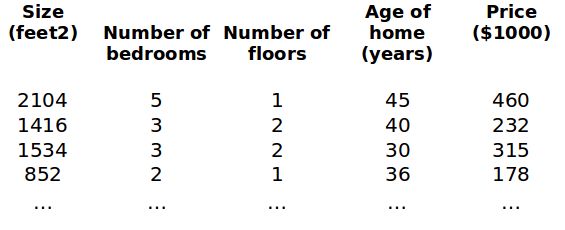
增添更多特征后,我们引入一系列新的注释:
n n n 代表特征的数量
x ( i ) {x^{\left( i \right)}} x(i)代表第 i i i 个训练实例,是特征矩阵中的第 i i i行,是一个向量(vector)。
比方说,上图的
x ( 2 ) = [ 1416 3 2 40 ] {x}^{(2)}\text{=}\begin{bmatrix} 1416\\\ 3\\\ 2\\\ 40 \end{bmatrix} x(2)= 1416 3 2 40 ,
x j ( i ) {x}_{j}^{\left( i \right)} xj(i)代表特征矩阵中第 i i i 行的第 j j j 个特征,也就是第 i i i 个训练实例的第 j j j 个特征。
如上图的 x 2 ( 2 ) = 3 , x 3 ( 2 ) = 2 x_{2}^{\left( 2 \right)}=3,x_{3}^{\left( 2 \right)}=2 x2(2)=3,x3(2)=2,
支持多变量的假设 h h h 表示为: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}} hθ(x)=θ0+θ1x1+θ2x2+...+θnxn,
这个公式中有 n + 1 n+1 n+1个参数和 n n n个变量,为了使得公式能够简化一些,引入 x 0 = 1 x_{0}=1 x0=1,则公式转化为: h θ ( x ) = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h_{\theta} \left( x \right)={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}} hθ(x)=θ0x0+θ1x1+θ2x2+...+θnxn
此时模型中的参数是一个 n + 1 n+1 n+1维的向量,任何一个训练实例也都是 n + 1 n+1 n+1维的向量,特征矩阵 X X X的维度是 m ∗ ( n + 1 ) m*(n+1) m∗(n+1)。
X = [ x 0 x 1 x 2 . . . x n ] {X}\text{=}\begin{bmatrix} x_0\\\ x_1\\\ x_2\\\ ...\\\ x_n \end{bmatrix} X= x0 x1 x2 ... xn θ = [ θ 0 θ 1 θ 2 . . . θ n ] {\theta}\text{=}\begin{bmatrix} \theta_0\\\ \theta_1\\\ \theta_2\\\ ...\\\ \theta_n \end{bmatrix} θ= θ0 θ1 θ2 ... θn
因此公式可以简化为: h θ ( x ) = θ T X h_{\theta} \left( x \right)={\theta^{T}}X hθ(x)=θTX,其中上标 T T T代表矩阵转置。
多变量梯度下降
参考视频: 4 - 2 - Gradient Descent for Multiple Variables (5 min).mkv
与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,则这个代价函数是所有建模误差的平方和,损失函数即: J ( θ 0 , θ 1 . . . θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( {\theta_{0}},{\theta_{1}}...{\theta_{n}} \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( h_{\theta} \left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}} J(θ0,θ1...θn)=2m1i=1∑m(hθ(x(i))−y(i))2 ,
其中模型为: h θ ( x ) = θ T X = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h_{\theta}\left( x \right)=\theta^{T}X={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}} hθ(x)=θTX=θ0+θ1x1+θ2x2+...+θnxn ,这里引入 x 0 = 1 x_0=1 x0=1
模型参数为: θ 0 θ 1 . . . θ n \theta_0 \ \ \theta_1 ...\theta_n θ0 θ1...θn
我们的目标和单变量线性回归问题中一样,是要找出使得代价函数最小的一系列参数。
多变量线性回归的批量梯度下降算法为:
即:
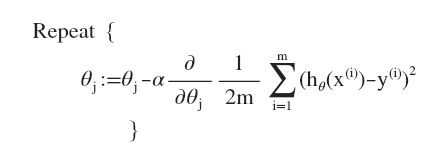
当 n > = 1 n>=1 n>=1时,
θ 0 : = θ 0 − a 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) {{\theta }_{0}}:={{\theta }_{0}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}x_{0}^{(i)} θ0:=θ0−am1i=1∑m(hθ(x(i))−y(i))x0(i)
θ 1 : = θ 1 − a 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 1 ( i ) {{\theta }_{1}}:={{\theta }_{1}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}x_{1}^{(i)} θ1:=θ1−am1i=1∑m(hθ(x(i))−y(i))x1(i)
θ 2 : = θ 2 − a 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 2 ( i ) {{\theta }_{2}}:={{\theta }_{2}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}})}x_{2}^{(i)} θ2:=θ2−am1i=1∑m(hθ(x(i))−y(i))x2(i)
我们开始随机选择一系列的参数值,计算所有的预测结果后,再给所有的参数一个新的值,如此循环直到收敛。
代码示例:
计算代价函数
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {h_{\theta}}\left( {x^{(i)}} \right)-{y^{(i)}} \right)}^{2}}} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
其中: h θ ( x ) = θ T X = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n {h_{\theta}}\left( x \right)={\theta^{T}}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}} hθ(x)=θTX=θ0x0+θ1x1+θ2x2+...+θnxn
Python 代码:
def computeCost(X, y, theta):
inner = np.power(((X * theta.T) - y), 2)
return np.sum(inner) / (2 * len(X))
梯度下降法实践1-特征缩放
参考视频: 4 - 3 - Gradient Descent in Practice I - Feature Scaling (9 min).mkv
在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0-2000平方英尺,而房间数量的值则是0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。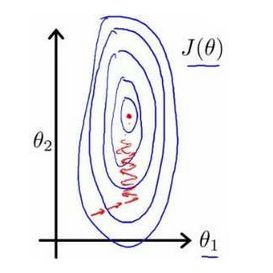
这里理解为横纵坐标差距太大导致的等高线形状为上图这样。
解决的方法是尝试将所有特征的尺度都尽量缩放到-1到1之间。如图: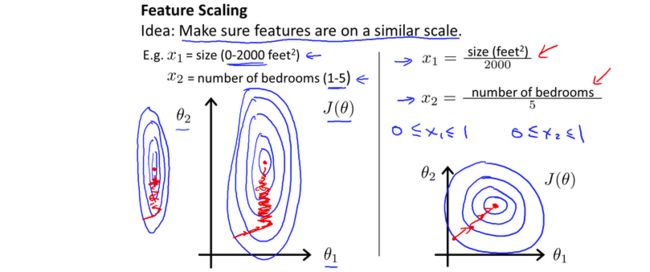
最简单的方法是令: x n = x n − μ n s n {{x}_{n}}=\frac{{{x}_{n}}-{{\mu}_{n}}}{{{s}_{n}}} xn=snxn−μn,其中 μ n {\mu_{n}} μn是平均值, s n {s_{n}} sn是标准差。
sn为特征值的范围
梯度下降法实践2-学习率
参考视频: 4 - 4 - Gradient Descent in Practice II - Learning Rate (9 min).mkv
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同,我们不能提前预知,我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。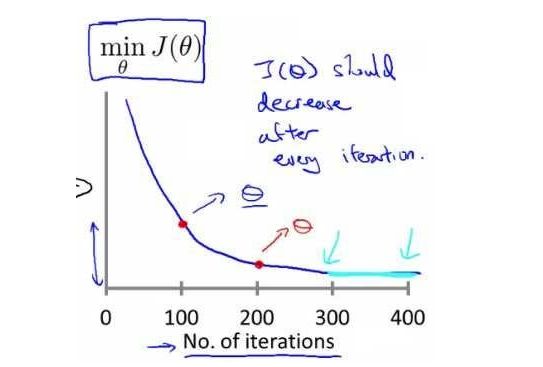
也有一些自动测试是否收敛的方法,例如将代价函数的变化值与某个阀值(例如0.001)进行比较,但通常看上面这样的图表更好。
梯度下降算法的每次迭代受到学习率的影响,如果学习率 a a a过小,则达到收敛所需的迭代次数会非常高;如果学习率 a a a过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。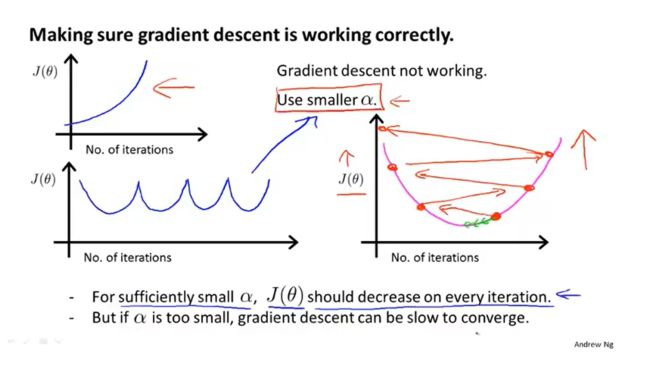
通常可以考虑尝试些学习率:
α = 0.01 , 0.03 , 0.1 , 0.3 , 1 , 3 , 10 \alpha=0.01,0.03,0.1,0.3,1,3,10 α=0.01,0.03,0.1,0.3,1,3,10
特征和多项式回归
参考视频: 4 - 5 - Features and Polynomial Regression (8 min).mkv
如房价预测问题,
h θ ( x ) = θ 0 + θ 1 × f r o n t a g e + θ 2 × d e p t h h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}\times{frontage}+{\theta_{2}}\times{depth} hθ(x)=θ0+θ1×frontage+θ2×depth
x 1 = f r o n t a g e {x_{1}}=frontage x1=frontage(临街宽度), x 2 = d e p t h {x_{2}}=depth x2=depth(纵向深度), x = f r o n t a g e ∗ d e p t h = a r e a x=frontage*depth=area x=frontage∗depth=area(面积),则: h θ ( x ) = θ 0 + θ 1 x {h_{\theta}}\left( x \right)={\theta_{0}}+{\theta_{1}}x hθ(x)=θ0+θ1x。
线性回归并不适用于所有数据,有时我们需要曲线来适应我们的数据,比如一个二次方模型: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 2 h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}^2} hθ(x)=θ0+θ1x1+θ2x22
或者三次方模型: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 2 + θ 3 x 3 3 h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}^2}+{\theta_{3}}{x_{3}^3} hθ(x)=θ0+θ1x1+θ2x22+θ3x33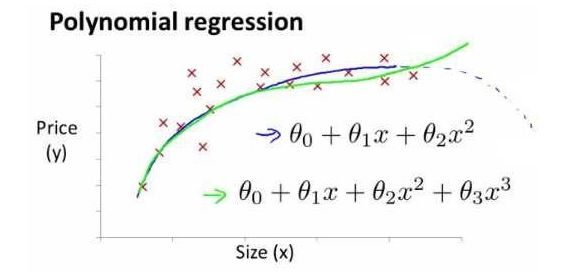
通常我们需要先观察数据然后再决定准备尝试怎样的模型(有时我们通过创建新的特征可能会得到一个更好的模型)。 另外,我们可以令:
x 2 = x 2 2 , x 3 = x 3 3 {{x}_{2}}=x_{2}^{2},{{x}_{3}}=x_{3}^{3} x2=x22,x3=x33,从而将模型转化为线性回归模型。
根据函数图形特性,我们还可以使:
h θ ( x ) = θ 0 + θ 1 ( s i z e ) + θ 2 ( s i z e ) 2 {{{h}}_{\theta}}(x)={{\theta }_{0}}\text{+}{{\theta }_{1}}(size)+{{\theta}_{2}}{{(size)}^{2}} hθ(x)=θ0+θ1(size)+θ2(size)2
或者:
h θ ( x ) = θ 0 + θ 1 ( s i z e ) + θ 2 s i z e {{{h}}_{\theta}}(x)={{\theta }_{0}}\text{+}{{\theta }_{1}}(size)+{{\theta }_{2}}\sqrt{size} hθ(x)=θ0+θ1(size)+θ2size
注:如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。可以使用算法决定使用什么特征,这里我想说的是你可自由选择特征。
正规方程
参考视频: 4 - 6 - Normal Equation (16 min).mkv
到目前为止,我们都在使用梯度下降算法,但是对于某些线性回归问题,正规方程方法是更好的解决方案。如:
正规方程是通过求解下面的方程来找出使得代价函数最小的参数的: ∂ ∂ θ j J ( θ j ) = 0 \frac{\partial}{\partial{\theta_{j}}}J\left( {\theta_{j}} \right)=0 ∂θj∂J(θj)=0 ,这里就是偏导数使其为0,求取局部最优解。
假设我们的训练集特征矩阵为 X X X(包含了 x 0 = 1 {{x}_{0}}=1 x0=1)并且我们的训练集结果为向量 y y y,则利用正规方程解出向量 θ = ( X T X ) − 1 X T y \theta ={{\left( {X^T}X \right)}^{-1}}{X^{T}}y θ=(XTX)−1XTy 。
上标T代表矩阵转置,上标-1 代表矩阵的逆。设矩阵 A = X T X A={X^{T}}X A=XTX,则: ( X T X ) − 1 = A − 1 {{\left( {X^T}X \right)}^{-1}}={A^{-1}} (XTX)−1=A−1
以下表示数据为例: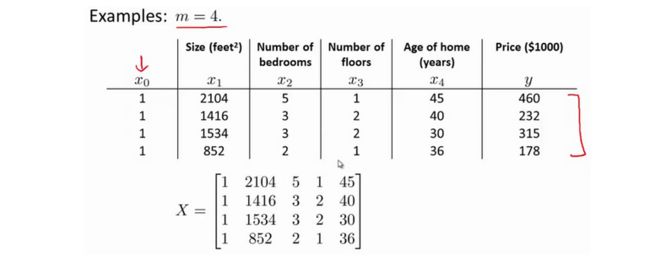
即:
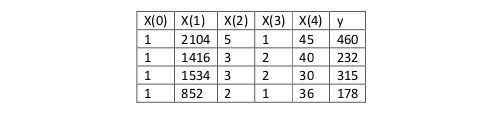
这里X=m*(n+1)矩阵,y为m的向量,m为训练样本数,n为特征数
运用正规方程方法求解参数:
在 Octave 中,正规方程写作:
pinv(X'*X)*X'*y
注:对于那些不可逆的矩阵(通常是因为特征之间不独立,如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征,也有可能是特征数量大于训练集的数量),正规方程方法是不能用的。
梯度下降与正规方程的比较:
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 α \alpha α | 不需要 |
| 需要多次迭代 | 一次运算得出 |
| 当特征数量 n n n大时也能较好适用 | 需要计算 ( X T X ) − 1 {{\left( {{X}^{T}}X \right)}^{-1}} (XTX)−1 如果特征数量n较大则运算代价大,因为矩阵逆的计算时间复杂度为 O ( n 3 ) O\left( {{n}^{3}} \right) O(n3),通常来说当 n n n小于10000 时还是可以接受的 |
| 适用于各种类型的模型 | 只适用于线性模型,不适合逻辑回归模型等其他模型 |
总结一下,只要特征变量的数目并不大,标准方程是一个很好的计算参数$\theta $的替代方法。具体地说,只要特征变量数量小于一万,我通常使用标准方程法,而不使用梯度下降法。
随着我们要讲的学习算法越来越复杂,例如,当我们讲到分类算法,像逻辑回归算法,我们会看到,实际上对于那些算法,并不能使用标准方程法。对于那些更复杂的学习算法,我们将不得不仍然使用梯度下降法。因此,梯度下降法是一个非常有用的算法,可以用在有大量特征变量的线性回归问题。或者我们以后在课程中,会讲到的一些其他的算法,因为标准方程法不适合或者不能用在它们上。但对于这个特定的线性回归模型,标准方程法是一个比梯度下降法更快的替代算法。所以,根据具体的问题,以及你的特征变量的数量,这两种算法都是值得学习的。
正规方程的python实现:
import numpy as np
def normalEqn(X, y):
theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X等价于X.T.dot(X)
return theta
正规方程及不可逆性(可选)
参考视频: 4 - 7 - Normal Equation Noninvertibility (Optional) (6 min).mkv
在这段视频中谈谈正规方程 ( normal equation ),以及它们的不可逆性。
由于这是一种较为深入的概念,并且总有人问我有关这方面的问题,因此,我想在这里来讨论它,由于概念较为深入,所以对这段可选材料大家放轻松吧,也许你可能会深入地探索下去,并且会觉得理解以后会非常有用。但即使你没有理解正规方程和线性回归的关系,也没有关系。
我们要讲的问题如下: θ = ( X T X ) − 1 X T y \theta ={{\left( {X^{T}}X \right)}^{-1}}{X^{T}}y θ=(XTX)−1XTy
备注:本节最后我把推导过程写下。
有些同学曾经问过我,当计算 θ \theta θ=inv(X'X ) X'y ,那对于矩阵 X ′ X X'X X′X的结果是不可逆的情况咋办呢?
如果你懂一点线性代数的知识,你或许会知道,有些矩阵可逆,而有些矩阵不可逆。我们称那些不可逆矩阵为奇异或退化矩阵。
问题的重点在于 X ′ X X'X X′X的不可逆的问题很少发生,在Octave里,如果你用它来实现 θ \theta θ的计算,你将会得到一个正常的解。在Octave里,有两个函数可以求解矩阵的逆,一个被称为pinv(),另一个是inv(),这两者之间的差异是些许计算过程上的,一个是所谓的伪逆,另一个被称为逆。使用pinv() 函数可以展现数学上的过程,这将计算出 θ \theta θ的值,即便矩阵 X ′ X X'X X′X是不可逆的。
在pinv() 和 inv() 之间,又有哪些具体区别呢 ?
其中inv() 引入了先进的数值计算的概念。例如,在预测住房价格时,如果 x 1 {x_{1}} x1是以英尺为尺寸规格计算的房子, x 2 {x_{2}} x2是以平方米为尺寸规格计算的房子,同时,你也知道1米等于3.28英尺 ( 四舍五入到两位小数 ),这样,你的这两个特征值将始终满足约束: x 1 = x 2 ∗ ( 3.28 ) 2 {x_{1}}={x_{2}}*{{\left( 3.28 \right)}^{2}} x1=x2∗(3.28)2。
实际上,你可以用这样的一个线性方程,来展示那两个相关联的特征值,矩阵 X ′ X X'X X′X将是不可逆的。
第二个原因是,在你想用大量的特征值,尝试实践你的学习算法的时候,可能会导致矩阵 X ′ X X'X X′X的结果是不可逆的。
具体地说,在 m m m小于或等于n的时候,例如,有 m m m等于10个的训练样本也有 n n n等于100的特征数量。要找到适合的 ( n + 1 ) (n +1) (n+1) 维参数矢量 θ \theta θ,这将会变成一个101维的矢量,尝试从10个训练样本中找到满足101个参数的值,这工作可能会让你花上一阵子时间,但这并不总是一个好主意。因为,正如我们所看到你只有10个样本,以适应这100或101个参数,数据还是有些少。
稍后我们将看到,如何使用小数据样本以得到这100或101个参数,通常,我们会使用一种叫做正则化的线性代数方法,通过删除某些特征或者是使用某些技术,来解决当 m m m比 n n n小的时候的问题。即使你有一个相对较小的训练集,也可使用很多的特征来找到很多合适的参数。
总之当你发现的矩阵 X ′ X X'X X′X的结果是奇异矩阵,或者找到的其它矩阵是不可逆的,我会建议你这么做。
首先,看特征值里是否有一些多余的特征,像这些 x 1 {x_{1}} x1和 x 2 {x_{2}} x2是线性相关的,互为线性函数。同时,当有一些多余的特征时,可以删除这两个重复特征里的其中一个,无须两个特征同时保留,将解决不可逆性的问题。因此,首先应该通过观察所有特征检查是否有多余的特征,如果有多余的就删除掉,直到他们不再是多余的为止,如果特征数量实在太多,我会删除些 用较少的特征来反映尽可能多内容,否则我会考虑使用正规化方法。
如果矩阵 X ′ X X'X X′X是不可逆的,(通常来说,不会出现这种情况),如果在Octave里,可以用伪逆函数pinv() 来实现。这种使用不同的线性代数库的方法被称为伪逆。即使 X ′ X X'X X′X的结果是不可逆的,但算法执行的流程是正确的。总之,出现不可逆矩阵的情况极少发生,所以在大多数实现线性回归中,出现不可逆的问题不应该过多的关注 X T X {X^{T}}X XTX是不可逆的。
增加内容:
θ = ( X T X ) − 1 X T y \theta ={{\left( {X^{T}}X \right)}^{-1}}{X^{T}}y θ=(XTX)−1XTy 的推导过程:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {h_{\theta}}\left( {x^{(i)}} \right)-{y^{(i)}} \right)}^{2}}} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
其中: h θ ( x ) = θ T X = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n {h_{\theta}}\left( x \right)={\theta^{T}}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}} hθ(x)=θTX=θ0x0+θ1x1+θ2x2+...+θnxn
将向量表达形式转为矩阵表达形式,则有 J ( θ ) = 1 2 ( X θ − y ) 2 J(\theta )=\frac{1}{2}{{\left( X\theta -y\right)}^{2}} J(θ)=21(Xθ−y)2 ,其中 X X X为 m m m行 n n n列的矩阵( m m m为样本个数, n n n为特征个数), θ \theta θ为 n n n行1列的矩阵, y y y为 m m m行1列的矩阵,对 J ( θ ) J(\theta ) J(θ)进行如下变换
J ( θ ) = 1 2 ( X θ − y ) T ( X θ − y ) J(\theta )=\frac{1}{2}{{\left( X\theta -y\right)}^{T}}\left( X\theta -y \right) J(θ)=21(Xθ−y)T(Xθ−y)
= 1 2 ( θ T X T − y T ) ( X θ − y ) =\frac{1}{2}\left( {{\theta }^{T}}{{X}^{T}}-{{y}^{T}} \right)\left(X\theta -y \right) =21(θTXT−yT)(Xθ−y)
= 1 2 ( θ T X T X θ − θ T X T y − y T X θ − y T y ) =\frac{1}{2}\left( {{\theta }^{T}}{{X}^{T}}X\theta -{{\theta}^{T}}{{X}^{T}}y-{{y}^{T}}X\theta -{{y}^{T}}y \right) =21(θTXTXθ−θTXTy−yTXθ−yTy)
接下来对 J ( θ ) J(\theta ) J(θ)偏导,需要用到以下几个矩阵的求导法则:
d A B d B = A T \frac{dAB}{dB}={{A}^{T}} dBdAB=AT
d X T A X d X = 2 A X \frac{d{{X}^{T}}AX}{dX}=2AX dXdXTAX=2AX
所以有:
∂ J ( θ ) ∂ θ = 1 2 ( 2 X T X θ − X T y − ( y T X ) T − 0 ) \frac{\partial J\left( \theta \right)}{\partial \theta }=\frac{1}{2}\left(2{{X}^{T}}X\theta -{{X}^{T}}y -{}({{y}^{T}}X )^{T}-0 \right) ∂θ∂J(θ)=21(2XTXθ−XTy−(yTX)T−0)
= 1 2 ( 2 X T X θ − X T y − X T y − 0 ) =\frac{1}{2}\left(2{{X}^{T}}X\theta -{{X}^{T}}y -{{X}^{T}}y -0 \right) =21(2XTXθ−XTy−XTy−0)
= X T X θ − X T y ={{X}^{T}}X\theta -{{X}^{T}}y =XTXθ−XTy
令 ∂ J ( θ ) ∂ θ = 0 \frac{\partial J\left( \theta \right)}{\partial \theta }=0 ∂θ∂J(θ)=0,
则有 θ = ( X T X ) − 1 X T y \theta ={{\left( {X^{T}}X \right)}^{-1}}{X^{T}}y θ=(XTX)−1XTy
需要用到的知识:
1.向量e的平方等于 e T e e^Te eTe
2.当两个矩阵相乘时,结果矩阵的对称性取决于原始矩阵的对称性。具体地说,如果矩阵 A 和矩阵 B 相乘得到矩阵 C,即 C = A * B,那么如果矩阵 A 是对称矩阵(Aᵀ = A),则矩阵 C 也是对称矩阵(Cᵀ = C)。
向量化
参考视频: 5 - 6 - Vectorization (14 min).mkv
在这段视频中,我将介绍有关向量化的内容,无论你是用Octave,还是别的语言,比如MATLAB或者你正在用Python、NumPy 或 Java C C++,所有这些语言都具有各种线性代数库,这些库文件都是内置的,容易阅读和获取,他们通常写得很好,已经经过高度优化,通常是数值计算方面的博士或者专业人士开发的。
而当你实现机器学习算法时,如果你能好好利用这些线性代数库,或者数值线性代数库,并联合调用它们,而不是自己去做那些函数库可以做的事情。如果是这样的话,那么通常你会发现:首先,这样更有效,也就是说运行速度更快,并且更好地利用你的计算机里可能有的一些并行硬件系统等等;其次,这也意味着你可以用更少的代码来实现你需要的功能。因此,实现的方式更简单,代码出现问题的有可能性也就越小。
举个具体的例子:与其自己写代码做矩阵乘法。如果你只在Octave中输入 a a a乘以 b b b就是一个非常有效的两个矩阵相乘的程序。有很多例子可以说明,如果你用合适的向量化方法来实现,你就会有一个简单得多,也有效得多的代码。
让我们来看一些例子:这是一个常见的线性回归假设函数: h θ ( x ) = ∑ j = 0 n θ j x j {{h}_{\theta }}(x)=\sum\limits_{j=0}^{n}{{{\theta }_{j}}{{x}_{j}}} hθ(x)=j=0∑nθjxj
如果你想要计算 h θ ( x ) h_\theta(x) hθ(x) ,注意到右边是求和,那么你可以自己计算 j = 0 j = 0 j=0 到$ j = n$ 的和。但换另一种方式来想想,把 h θ ( x ) h_\theta(x) hθ(x) 看作 θ T x \theta^Tx θTx,那么你就可以写成两个向量的内积,其中 θ \theta θ就是 θ 0 \theta_0 θ0、 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2,如果你有两个特征量,如果 n = 2 n = 2 n=2,并且如果你把 x x x 看作 x 0 x_0 x0、 x 1 x_1 x1、 x 2 x_2 x2,这两种思考角度,会给你两种不同的实现方式。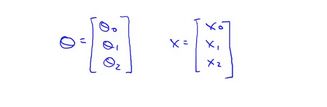
比如说,这是未向量化的代码实现方式:
计算 h θ ( x ) h_\theta(x) hθ(x)是未向量化的,我们可能首先要初始化变量 p r e d i c t i o n prediction prediction 的值为0.0,而这个变量 p r e d i c t i o n prediction prediction 的最终结果就是 h θ ( x ) h_\theta(x) hθ(x),然后我要用一个 for 循环, j j j 取值 0 到 n + 1 n+1 n+1,变量 p r e d i c t i o n prediction prediction 每次就通过自身加上$ theta(j) $乘以 x ( j ) x(j) x(j)更新值,这个就是算法的代码实现。
顺便我要提醒一下,这里的向量我用的下标是0,所以我有 θ 0 \theta_0 θ0、 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2,但因为MATLAB的下标从1开始,在 MATLAB 中 θ 0 \theta_0 θ0,我们可能会用 t h e t a ( 1 ) theta(1) theta(1) 来表示,这第二个元素最后就会变成, t h e t a ( 2 theta(2 theta(2) 而第三个元素,最终可能就用 t h e t a ( 3 ) theta(3) theta(3)表示,因为MATLAB中的下标从1开始,这就是为什么这里我的 for 循环, j j j取值从 1 直到 n + 1 n+1 n+1,而不是从 0 到 n n n。这是一个未向量化的代码实现方式,我们用一个 for 循环对 n n n 个元素进行加和。
作为比较,接下来是向量化的代码实现:
你把x和 θ \theta θ看做向量,而你只需要令变量 p r e d i c t i o n prediction prediction等于 t h e t a theta theta转置乘以 x x x,你就可以这样计算。与其写所有这些for循环的代码,你只需要一行代码,这行代码就是利用 Octave 的高度优化的数值,线性代数算法来计算两个向量 θ \theta θ以及 x x x的内积,这样向量化的实现更简单,它运行起来也将更加高效。这就是 Octave 所做的而向量化的方法,在其他编程语言中同样可以实现。
与此相反,使用较好的**C++数值线性代数库,你可以写出像右边这样的代码,因此取决于你的数值线性代数库的内容。你只需要在C++**中将两个向量相乘,根据你所使用的数值和线性代数库的使用细节的不同,你最终使用的代码表达方式可能会有些许不同,但是通过一个库来做内积,你可以得到一段更简单、更有效的代码。
现在,让我们来看一个更为复杂的例子,这是线性回归算法梯度下降的更新规则: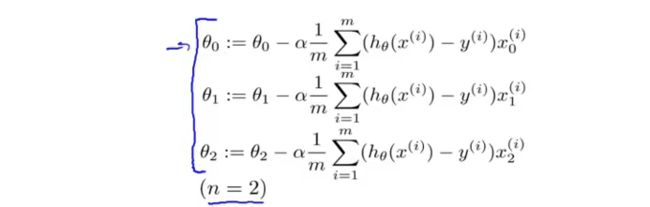
我们用这条规则对$ j$ 等于 0、1、2等等的所有值,更新对象 θ j \theta_j θj,我只是用 θ 0 \theta_0 θ0、 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2来写方程,假设我们有两个特征量,所以 n n n等于2,这些都是我们需要对 θ 0 \theta_0 θ0、 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2进行更新,这些都应该是同步更新,我们用一个向量化的代码实现,这里是和之前相同的三个方程,只不过写得小一点而已。
你可以想象实现这三个方程的方式之一,就是用一个 for 循环,就是让 j j j等于0、等于1、等于2,来更新 θ j \theta_j θj。但让我们用向量化的方式来实现,看看我们是否能够有一个更简单的方法。基本上用三行代码或者一个for 循环,一次实现这三个方程。让我们来看看怎样能用这三步,并将它们压缩成一行向量化的代码来实现。做法如下:
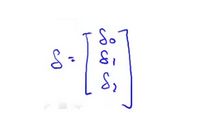
我打算把 θ \theta θ看做一个向量,然后我用 θ \theta θ- α \alpha α 乘以某个别的向量 δ \delta δ 来更新 θ \theta θ。
让我解释一下是怎么回事:我要把 θ \theta θ看作一个向量,有一个 n + 1 n+1 n+1 维向量, α \alpha α 是一个实数, δ \delta δ在这里是一个向量。
所以这个减法运算是一个向量减法,因为 α \alpha α 乘以 δ是一个向量,所以 θ \theta θ就是 θ \theta θ - α δ \alpha \delta αδ得到的向量。
那么什么是向量 δ \delta δ 呢 ?
X ( i ) X^{(i)} X(i)是一个向量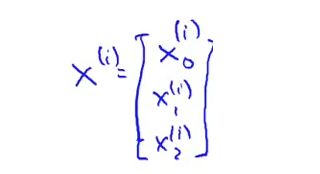
你就会得到这些不同的式子,然后作加和。
实际上,在以前的一个小测验,如果你要解这个方程,我们说过为了向量化这段代码,我们会令u = 2v +5w因此,我们说向量 u u u等于2乘以向量 v v v加上5乘以向量 w w w。用这个例子说明,如何对不同的向量进行相加,这里的求和是同样的道理。
这就是为什么我们能够向量化地实现线性回归。
所以,我希望步骤是有逻辑的。请务必看视频,并且保证你确实能理解它。如果你实在不能理解它们数学上等价的原因,你就直接实现这个算法,也是能得到正确答案的。所以即使你没有完全理解为何是等价的,如果只是实现这种算法,你仍然能实现线性回归算法。如果你能弄清楚为什么这两个步骤是等价的,那我希望你可以对向量化有一个更好的理解,如果你在实现线性回归的时候,使用一个或两个以上的特征量。
有时我们使用几十或几百个特征量来计算线性归回,当你使用向量化地实现线性回归,通常运行速度就会比你以前用你的for循环快的多,也就是自己写代码更新 θ 0 \theta_0 θ0、 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2。
因此使用向量化实现方式,你应该是能够得到一个高效得多的线性回归算法。而当你向量化我们将在之后的课程里面学到的算法,这会是一个很好的技巧,无论是对于Octave 或者一些其他的语言 如C++、Java 来让你的代码运行得更高效。
作业练习
知识补充
作业描述
多元线性回归
如果你已经成功地完成了上面的材料,祝贺你!你现在了解了线性回归,应该能够开始在您的
自己的数据集。对于本编程练习的其余部分,我们包括以下内容可选练习。这些练习将帮助你更深入地了解如果您有能力,我们鼓励您完成他们也是。
在本部分中,您将使用多个变量实现线性回归,以预测房价。假设你正在出售你的房子,而你想知道什么是好的市场价格。一种方法是首先收集最近出售的房屋的信息,并制作房屋模型价格。
文件ex1data2.txt包含俄勒冈州波特兰市的房价培训集。第一列是房子的大小(平方英尺)第二列是卧室数量,第三列是价格房子的一部分。
特征标准化
ex1 multi.m脚本将从加载并显示一些值开始来自该数据集。通过查看这些值,请注意房屋大小约为
卧室数量的1000倍。当特征相差几个数量级时,首先进行特征缩放可以使梯度下降收敛更快。
您在这里的任务是完成featureNormalize.m中的代码以
•从数据集中减去每个特征的平均值。
•减去平均值后,再对特征值进行缩放(除法)
通过它们各自的\标准偏差。标准偏差是一种衡量变化程度的方法,在特定特征的值范围内(大多数数据点将位于
平均值的±2个标准偏差);这是一个替代范围的值(最大值-最小值)。在Octave/MATLAB中,您可以使用\std“函数计算标准偏差。例如,在featureNormalize.m内部,数量X(:,1)包含训练中x1(房屋大小)的所有值设置,所以std(X(:,1))计算房屋尺寸的标准偏差。调用featureNormalize.m时,1的额外列对应于x0=1尚未被添加到X(参见ex1 multi.m详细信息)。
以前,您在单变量回归问题上实现了梯度下降。现在唯一的区别是矩阵X中还有一个特征。假设函数和批量梯度下降更新规则保持不变。
注意随着学习率的变化收敛曲线的变化。在学习率很低的情况下,你应该会发现梯度下降需要收敛到最优值的时间很长。相反,通过大学习速率、梯度下降可能不会收敛,甚至可能发散!
使用您发现的最佳学习率,运行ex1 multi.m脚本运行梯度下降直到收敛,以找到θ的最终值。下一个用这个θ值来预测1650平方英尺的房子的价格3间卧室。稍后将使用值检查正规方程。制作时不要忘记规范化功能这个预测!
在讲座视频中,您了解到线性的闭式解回归是:
θ = ( X T X ) − 1 X T y ⃗ θ = (X^T X)^{−1} X^T\vec{y} θ=(XTX)−1XTy
使用此公式不需要任何特征缩放,您将得到一次计算的精确解:在收敛之前没有循环在梯度下降中。
完成normalEqn.m中的代码,使用上面的公式计算θ。请记住,虽然您不需要缩放功能,但我们仍然需要将一列1添加到X矩阵以具有截距项(θ0)。ex1.m中的代码将为您将1的列添加到X中。
可选(未分级)练习:现在,一旦你找到θ,就用这个方法,用它来预测一栋1650平方英尺的房子的价格3间卧室。你应该会发现,它给出的预测价格与价值相同.您使用具有梯度下降的模型拟合获得(见第3.2.1节)。
作业提交路径
这个作业集成到上篇笔记的路径了
作业思路
相关内容
- ML-AndrewNg-Notes