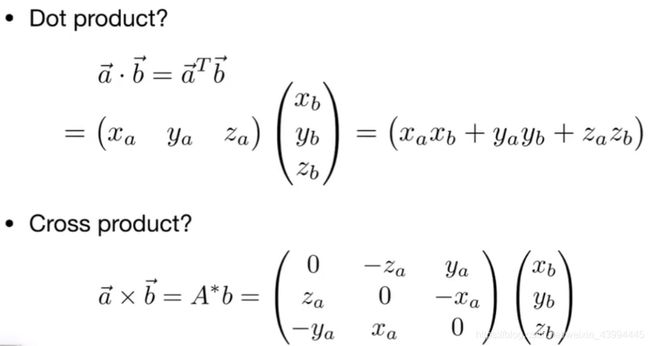向量的点乘 a·b 和叉乘 a×b

点乘:

点乘, 即|a|·|b|·cosθ, (结果是一个数字)
即: a的长度 * b的长度 * ab的夹角

夹角<90°, 则cosθ>0, 则结果>0
夹角>90°, 则cosθ<0, 则结果<0

那有什么用呢?

答: 判断敌人在我前面还是后面

我向前方发一条射线, 作为向量a
我向敌人发一条射线, 作为向量b
计算点乘结果
如果是正, 即夹角小于90°, 即敌人在我面前180°内
如果是负, 即夹角大于90°, 即敌人在我身后180°内

Vector3 a = me.forward;
Vector3 b = enemy.position - me.position;
float dot = Vector3.Dot(a, b);
if(dot > 0)
{
	//敌人在我前边
}

还有什么用处呢?

1.求b在a上的投影长度
因为: a·b = |a|·|b|·cosθ
又因为: 投影长度 = |b|·cosθ
则: 投影长度 = a·b ÷ |a|

2.求θ的角度
已知a·b的情况下
cosθ = a·b ÷ |a| ÷ |b|
再用反余弦, 就能求θ的角度

叉乘:

叉乘的结果是个向量
此向量垂直于ab向量所在的平面
冲上或者冲下

用来判断敌人在我左边还是右边

我向前方发一条射线, 作为向量a
我向敌人发一条射线, 作为向量b
叉乘的结果要么冲上, 要么冲下
看y轴的正负就知道是左边还是右边了

Vector3 a = me.forward;
Vector3 b = enemy.position - me.position;
Vector3 cross = Vector3.Cross(a, b);
if(cross.y > 0)
{
	//敌人在我的......左还是右来着, 忘了
}

叉乘是按照右手定则算的, 而Unity是左手坐标系, 所以结果是相反的, 所以正就是负, 负就是正
(右手定则, 如图, 3个向量相互垂直, 已知其中2个就能确定第3个, 具体是怎么算的, 自己去看百度百科)

其实点乘也可以判左右

//区别就是这次以我的右手方向(me.right)作为向量a

Vector3 a = me.right;
Vector3 b = enemy.position - me.position;
float dot = Vector3.Dot(a, b);
if(dot > 0)
{
	//敌人在我右边
}
else
{
    //敌人在我左边
}

在不能转身的2D游戏里一般用不到这些点乘叉乘什么的

如果你在我左边, 则, 你的x必然小于我的x

if(you.position.x < me.position.x)
{
	//你在我左边
}

---

以下是从哔哩哔哩<现代计算机图形学入门>看到的

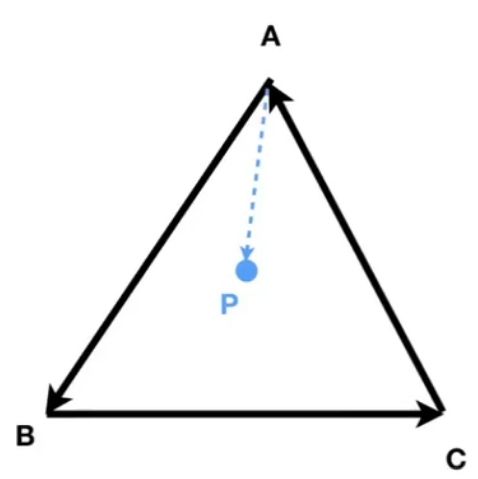
用来判断点是否在三角内

判断点P是否在三角形ABC内:

先做成3个首尾相交的向量AB, BC, CA
先AB×AP, 好, AP在左侧
再BC×BP, 好, 还是BP在左侧
再CA×CP, 好, 还是CP在左侧
好, 都在左侧
证得: P在三角形内

问: 那如果ABC 3个点是顺时针排布的呢?
答: 那就看是否都在右侧
问: 那我们怎么知道他是顺时针还是逆时针呢?
答: 我们不需要知道, 只要是同左或者同右, 就可以判定: 点在三角形内

注意: 还有点P刚好在三角形边上的情况, 那种另外算
注意: 该方法可适用于所有的"凸多边形"

点乘和点乘的矩阵表示: