动手学深度学习(一)预备知识
目录
一、数据操作
1. N维数组样例
2. 访问元素
3. 基础函数
(1) 创建一个行向量
(2)通过张量的shape属性来访问张量的形状和元素总数
(3)reshape()函数
(4)创建全0、全1、其他常量或从特定分布中随机采样的数字组成的张量
(5)标准运算(张量间的标准运算,都是按元素运算)
(6)拼接函数cat
(7)求和函数sum
(8)矩阵的转置
(9)复制张量
(10)点积,矩阵-向量积和矩阵乘法
(11)范数
4.广播机制
5.转化为Numpy张量
课程推荐:跟李沐学AI的个人空间-跟李沐学AI个人主页-哔哩哔哩视频
一、数据操作
1. N维数组样例
(1)0-d 标量
1.0(2)1-d 向量
[1.0, 2.7, 3.4](3)2-d 矩阵
[[1.0, 2.7, 3.4]
[5.0, 0.2, 4.6]
[4.3, 8.5, 0.2]](4)3-d RGB图片(CxHxW)
[[[1.0,2.7,3.4]
[5.0,0.2,4.6]
[4.3,8.5,0.2]]
[[3.2, 5.7, 3.4]
[5.4, 6.2, 3.2]
[4.1, 3.5, 6.2]]](5)4-d 一个RGB图片批量(BxCxHxW)
(6)5-d 一个视频批量(TxBxCxHxW)
2. 访问元素
切片规则:[start : end : step]
start : 起始索引,从0开始,-1表示结束。
end:结束索引,不包含。
step:步长,即范围内每次取值的间隔;步长为正时,从左向右取值。步长为负时,反向取值。
(1)访问一个元素
[1, 2]
>>> x = torch.arange(1, 17).reshape(4, 4)
>>> x[1, 2]
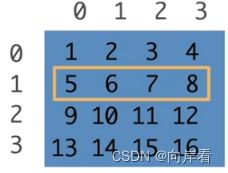
tensor(7)(2)访问一行
[1,:]
>>> x[1,:]
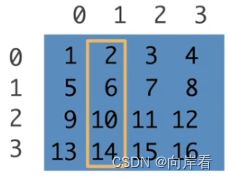
tensor([5, 6, 7, 8])(3)访问一列
[:,1]
>>> x[:,1]
tensor([ 2, 6, 10, 14])(4)子区域
[1:3,1:]
>>> x[1:3,1:]
tensor([[ 6, 7, 8],
[10, 11, 12]])[::3,::2]
>>> x[::3,::2]
tensor([[ 1, 3],
[13, 15]])3. 基础函数
(1) 创建一个行向量
x = torch.arange(12)
x #tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])(2)通过张量的shape属性来访问张量的形状和元素总数
x.shape # torch.Size([12])
x.size() # torch.Size([12])(3)reshape()函数
改变一个张量的形状 。
X = x.reshape(3,4)
X
# tensor([[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11]])(4)创建全0、全1、其他常量或从特定分布中随机采样的数字组成的张量
全0: 第一个参数为张量的shape。
torch.zeros((2,3,4))
# tensor([[[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]],
# [[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]]])
全1:
torch.ones((1,3,4))
# tensor([[[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]]])
其他常量(指定值):
torch.tensor([[1,2],[2,1]])
# tensor([[1, 2],
# [2, 1]])(5)标准运算(张量间的标准运算,都是按元素运算)
x = torch.tensor([1.0, 2, 3, 4])
y = torch.tensor([5, 6, 7, 8])
x+y,x-y,x*y,x/y,x**y
# (tensor([ 6., 8., 10., 12.]), tensor([-4., -4., -4., -4.]), tensor([ 5., 12., 21., 32.]), tensor([0.2000, 0.3333, 0.4286, 0.5000]), tensor([1.0000e+00, 6.4000e+01, 2.1870e+03, 6.5536e+04]))
比较运算符,按位比较
x == y
# tensor([False, False, False, False]) * 按位相乘,称为哈达玛乘(数学符号![]() )。
)。
>>> A = torch.arange(9).reshape(3,3)
>>> A
tensor([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
>>> B = torch.arange(9,18).reshape(3,3)
>>> B
tensor([[ 9, 10, 11],
[12, 13, 14],
[15, 16, 17]])
>>> A * B
tensor([[ 0, 10, 22],
[ 36, 52, 70],
[ 90, 112, 136]])(6)拼接函数cat
torch.cat(inputs, dim=?)
- inputs : 待连接的张量序列,可以是任意相同
Tensor类型的python 序列- dim : 选择的扩维, 必须在
0到len(inputs[0])之间,沿着此维连接张量序列。
dim=0,表示按第0维方向拼接,即按行方向拼接;dim=1,表示按第0维方向拼接,即按列方向拼接;dim=3……
y = torch.tensor(([[4, 1],[3, 5]]))
x = torch.arange(4, dtype=torch.float32).reshape(2, 2)
torch.cat((x, y), dim=0)
# tensor([[0., 1.],
# [2., 3.],
# [4., 1.],
# [3., 5.]])
torch.cat((x, y), dim=1)
# tensor([[0., 1., 4., 1.],
# [2., 3., 3., 5.]])
(7)求和函数sum
参数1,axis:指定求和维度,张量按该维度求和,并将该维度消去。
如,张量形状为[2, 5, 4],axis=0时,求和后,张量形状为[5, 4]。
参数2,keepdims:默认为False,是否保留axis要消去的维度。keepdims=True时,将要消去的维度长度置为1。
如,张量形状为[2, 5, 4],axis=0,keepdims=True时,求和后,张量形状为[1,5, 4]。
1)张量中的所有元素求和:
x = torch.tensor([1.0, 2, 3, 4])
x.sum()
# tensor(10.)2)按行(第0维)求和:
>>> A = torch.arange(9).reshape(3,3)
>>> A
tensor([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
>>> A.sum(axis=0)
tensor([ 9, 12, 15])3)按列(第1维)求和:
>>> A.sum(axis=1)
tensor([ 3, 12, 21])2维求和,3维……
4)keepdims(保留维度):
按某一维度求和时,保留该维度,该维度长度置为1。
>>> A
tensor([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
>>> A.sum(axis=1).size()
torch.Size([3])
>>> A.sum(axis=1,keepdims=True).size()
torch.Size([3, 1])
>>> A.sum(axis=1,keepdims=True)
tensor([[ 3],
[12],
[21]])
# 按列求均值
>>> A/A.sum(axis=1,keepdims=True)
tensor([[0.0000, 0.3333, 0.6667],
[0.2500, 0.3333, 0.4167],
[0.2857, 0.3333, 0.3810]])5)指定多维度求和
A.sum(axis=[n, m]),按n和m维度求和,求和结果中其他维度不变,将n,m维度消去。
>>> A = torch.arange(8).reshape(2,2,2)
>>> A
tensor([[[0, 1],
[2, 3]],
[[4, 5],
[6, 7]]])
# 保留第1维度
>>> A.sum(axis=[0,2]).size()
torch.Size([2])
# 使用keepdims保留要消去的维度,将维度长度置为1
>>> A.sum(axis=[0,2],keepdims=True).size()
torch.Size([1, 2, 1])
# 输出
>>> A.sum(axis=[0,2])
tensor([10, 18])
(8)矩阵的转置
>>> import torch
>>> B = torch.tensor(([1,2,3],[4,5,6],[7,8,9]))
>>> B
tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
>>> B.T
tensor([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]])(9)复制张量
“=”,复制之后的两个张量共用一个内存地址。
>>> A = B
>>> id(B)
1950198475976
>>> id(A)
1950198475976
>>> B[0]=10
>>> B
tensor([10, 2, 3, 4, 5, 6, 7, 8, 9])
>>> A
tensor([10, 2, 3, 4, 5, 6, 7, 8, 9])clone(),重新分配内存地址。
>>> A=B.clone()
>>> id(A)
1950198519512
>>> id(B)
1950198475976(10)点积,矩阵-向量积和矩阵乘法
向量点积—dot函数(1维):
>>> A = torch.arange(4)
>>> A
tensor([0, 1, 2, 3])
>>> B
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
>>> B = torch.arange(4, 8)
>>> B
tensor([4, 5, 6, 7])
>>> torch.dot(A, B)
tensor(38)矩阵点积(2维):
按位相乘求和。
>>> A = torch.arange(9).reshape(3,3)
>>> B = torch.arange(9,18).reshape(3,3)
>>> torch.sum(A * B)
tensor(528)矩阵-向量积(mv函数):
>>> B = torch.arange(9,18).reshape(3,3)
>>> C = torch.arange(3)
>>> torch.mv(B, C)
tensor([32, 41, 50])矩阵乘法(mm函数):
>>> torch.mm(A, B)
tensor([[ 42, 45, 48],
[150, 162, 174],
[258, 279, 300]])(11)范数
L1范数:
向量元素的绝对值之和。
>>> u = torch.tensor([3.0, -4.0])
>>> torch.abs(u).sum()
tensor(7.)L2范数:
向量元素平方和的平方根。
>>> u = torch.tensor([3.0, -4.0])
>>> torch.norm(u)
tensor(5.)弗罗贝尼乌斯-范数(F-范数):
矩阵元素的平方和的平方根。
>>> torch.norm(torch.ones(4, 9))
tensor(6.)4.广播机制
1.通过适当复制元素来扩展一个或两个数组,以便在转换之后,两个张量具有相同的形状。
2.对于生成的数组执行按元素操作。
y = torch.arange(12).reshape(3,2,2)
y
# tensor([[[ 0, 1],
# [ 2, 3]],
#
# [[ 4, 5],
# [ 6, 7]],
# [[ 8, 9],
# [10, 11]]])
x = torch.tensor([[1,2],[3,4]])
x
# tensor([[1, 2],
# [3, 4]])
x + y
# tensor([[[ 1, 3],
# [ 3, 5]],
# [[ 5, 7],
# [ 7, 9]],
# [[ 9, 11],
# [11, 13]]])5.转化为Numpy张量
A = x.numpy()
type(A)
#