【卷积神经网络--卷积/池化后特征图大小计算公式】
【卷积神经网络–卷积/池化后特征图大小计算公式】
参考链接: 卷积神经网络系列之卷积/池化后特征图大小怎么计算??
torch中的Conv2d卷积的输入的Tensor张量是:[batch, channel, height, width]),Conv2d卷积包含的参数如下:
class Conv2d(_ConvNd):
def __init__(
self,
in_channels: int, # 输入通道数
out_channels: int, # 输出通道数
kernel_size: _size_2_t, # 卷积核尺寸
stride: _size_2_t = 1, # 移动步长
padding: Union[str, _size_2_t] = 0, # 填充0的个数
dilation: _size_2_t = 1, # 在Pytorch中,dilation = 1等同于没有dilation的标准卷积
groups: int = 1,
bias: bool = True,
padding_mode: str = 'zeros', # TODO: refine this type
device=None,
dtype=None
)
dilation(扩张):
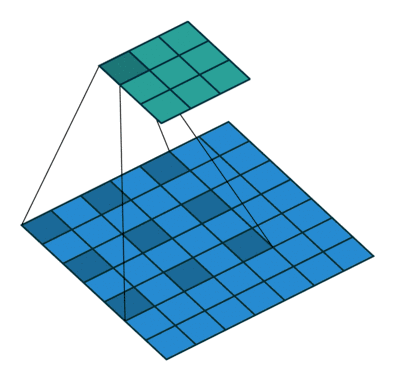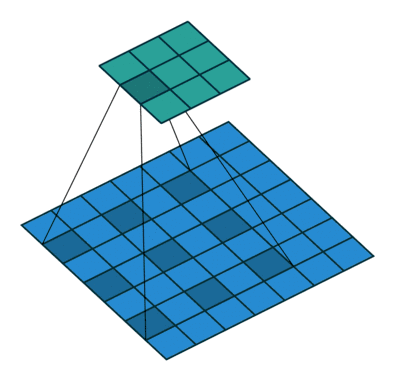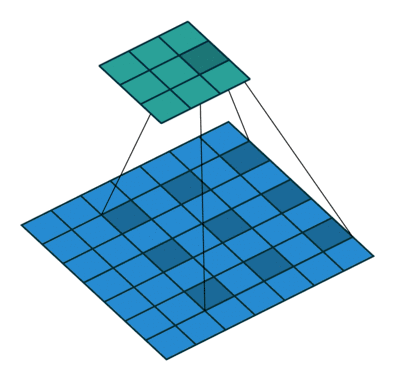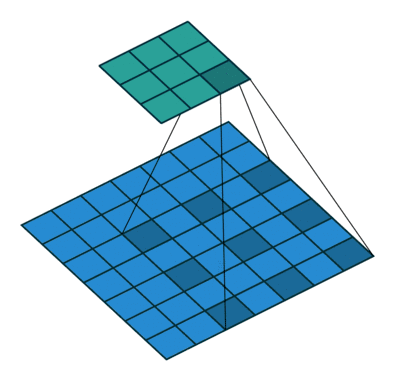
在Pytorch中,dilation = 1等同于没有dilation的标准卷积,观察下方动态图可以发现,原来的3x3卷积核,上下左右各插入2个空格,扩张成5x5的卷积核,
空洞卷积(atrous convolutions)又名扩张卷积(dilated convolutions),向卷积层引入了一个称为“ 扩张率(dilation rate)”的新参数,该参数定义了卷积核处理数据时各值的间隔。
在相同的计算条件下,空洞卷积提供了更大的感受野。空洞卷积经常用在实时图像分割中。当网络层需要较大的感受野,但计算资源有限而无法提高卷积核数量或大小时,可以考虑空洞卷积。
groups:
当groups=1的时候,假设此时 输入的通道数为n,输出的通道数为m,那么理解为把输入的通道分成1组(不分组),每一个输出通道需要在所有的输入通道上做卷积,也就是一种参数共享的局部全连接。
如果把groups改成2,可以理解为把 输入的通道分成两组,此时每一个输出通道只需要在其中一组上做卷积。
如果groups=in_channels,也就是把 输入的通道分成in_channels组(每一组也就一个通道),此时每一个输出通道只需要在其中一个输入通道上做卷积。
1、卷积后的特征图大小公式:
o u t p u t s i z e = [ ( i n p u t s i z e − k e r n e l s i z e + 2 ∗ p a d d i n g ) / s t r i d e ] + 1 output_{size}=[(input_{size}-kernel_{size}+2*padding)/stride]+1 outputsize=[(inputsize−kernelsize+2∗padding)/stride]+1,
(向下取整)
如:28x28的手写数字图片,input_size=28,kernel_size=3,padding=1,stride=3,output_size=[(28-3+2*1)/3]+1=10
引入dilation(扩张)后,特征图的尺寸计算公式变为:
o u t p u t s i z e = [ ( i n p u t s i z e − ( d i l a t i o n ∗ ( k e r n e l s i z e − 1 ) + 1 ) + 2 ∗ p a d d i n g ) / s t r i d e ] + 1 output_{size}=[(input_{size}-(dilation *(kernel_{size}-1)+1)+2 *padding )/stride ]+1 outputsize=[(inputsize−(dilation∗(kernelsize−1)+1)+2∗padding)/stride]+1 ,
(向下取整)
新的 k e r n e l s i z e kernel_{size} kernelsize就变成了:
n e w k e r n e l s i z e = d i l a t i o n ∗ ( k e r n e l s i z e − 1 ) + 1 newkernel_{size}=dilation *(kernel_{size}-1)+1 newkernelsize=dilation∗(kernelsize−1)+1
所以,
o u t p u t s i z e = [ ( i n p u t s i z e − n e w k e r n e l s i z e + 2 ∗ p a d d i n g ) / s t r i d e ] + 1 output_{size}=[(input_{size}-newkernel_{size}+2 *padding )/stride ]+1 outputsize=[(inputsize−newkernelsize+2∗padding)/stride]+1 ,
(向下取整)
2、池化后的特征图大小计算公式:
class MaxPool2d(_MaxPoolNd):
kernel_size: _size_2_t
stride: _size_2_t
padding: _size_2_t
dilation: _size_2_t
def forward(self, input: Tensor):
return F.max_pool2d(input, self.kernel_size, self.stride,
self.padding, self.dilation, ceil_mode=self.ceil_mode,
return_indices=self.return_indices)
计算公式如下:
o u t p u t s i z e = ( i n p u t s i z e − k e n e l s i z e ) / s t r i d e + 1 output_{size} = (input_{size} - kenel_{size})/ stride + 1 outputsize=(inputsize−kenelsize)/stride+1,(向下取整)
如:前面输出10的尺寸再池化,input_size=10,kernel_size=2,stride=2,output_size=(10-2)/2+1=5
3、转置卷积(反卷积)输出尺寸:
转置卷积俗称反卷积,但正规叫法是转置卷积。是上采样方式中的一种。
转置卷积用来增大特征图的分辨率。
o u t p u t s i z e = ( i n p u t s i z e − 1 ) ∗ s t r i d e − 2 ∗ p a d d i n g + k e r n e l s i z e output_{size} = (input_{size}-1)*stride -2* padding+kernel_{size} outputsize=(inputsize−1)∗stride−2∗padding+kernelsize
如:前面卷积输出10的尺寸,再反卷积,input_size=5,kernel_size=3,stride=3,padding=1,output_size=(10-1)*3-2*1+3=28回到原来的28尺寸。
1. 在tensorflow中:如果你想要输出等于输入,padding="SAME"即可,如果你想要输出别的尺寸的特征图,使用padding=‘VALID’,conv2d会自动计算输出特征图大小。
2. 在pytorch中:pytorch里面没有same和valid,所以你想要保持输出等于输入,要利用pad=t,t为填充尺寸,以保持输入输出特征图相等。