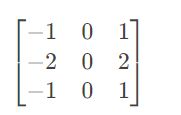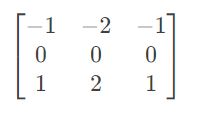Sobel边缘检测算法

1、算法概述

        Sobel边缘检测算法比较简单，实际应用中效率比canny边缘检测效率要高，但是边缘不如Canny检测的准确，然而在很多实际应用的场合，sobel边缘却是首选，Sobel算子是高斯平滑与微分操作的结合体，所以其抗噪声能力很强，用途较多。尤其是在对效率要求较高，而对细纹理不太关系的时候。
   使用Sobel算子提取图像边缘分3个步骤：

1.提取X方向的边缘，X方向一阶Sobel边缘检测算法为：

2.提取Y方向的边缘，Y方向一阶Sobel边缘检测算法为：

 3.综合两个方向的边缘信息得到整幅图像的边缘。

2、主要函数

Sobel_x_or_y = cv2.Sobel(src, ddepth, dx, dy, dst, ksize, scale, delta, borderType)

• src：传入的图像
• ddepth：图像的深度
• dx、dy：指的是求导的阶数，0表示这个方向上没有求导，所填的数一般为0、1、2。
• ksize：是Sobel算子的大小，即卷积核的大小，必须为奇数1、3、5、7。如果ksize=-1，就演变成为3x3的Scharr算子，scale是缩放导数的比例常数，默认情况为没有伸缩系数。
• borderType：是判断图像边界的模式，这个参数默认值为cv2.BORDER_DEFAULT。
• dst及dst之后的参数都是可选参数。

3、代码展示 

#!/usr/bin/env python
#coding=utf-8

import cv2
import numpy as np

img = cv2.imread("../img/lrn.jpg", 0)
'''
Sobel函数求完导数后会有负值，还有会大于255的值。
而原图像是uint8，即8位无符号数(范围在[0,255])，所以Sobel建立的图像位数不够，会有截断。
因此要使用16位有符号的数据类型，即cv2.CV_16S。
''' 
x = cv2.Sobel(img, cv2.CV_16S, 1, 0)
y = cv2.Sobel(img, cv2.CV_16S, 0, 1)
'''
在经过处理后，别忘了用convertScaleAbs()函数将其转回原来的uint8形式。
否则将无法显示图像，而只是一副灰色的窗口。
dst = cv2.convertScaleAbs(src[, dst[, alpha[, beta]]])  
其中可选参数alpha是伸缩系数，beta是加到结果上的一个值。结果返回uint8类型的图片。
'''
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
'''
由于Sobel算子是在两个方向计算的，最后还需要用cv2.addWeighted(...)函数将其组合起来
。其函数原型为：
dst = cv2.addWeighted(src1, alpha, src2, beta, gamma[, dst[, dtype]])  
其中alpha是第一幅图片中元素的权重，beta是第二个的权重，
gamma是加到最后结果上的一个值。
'''
dst = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
cv2.imshow("absX,absY,Result", np.hstack([absX,absY,dst]))
cv2.waitKey(0)

效果展示：

代码展示： 

#!/usr/bin/env python
# encoding=gbk

import cv2
from matplotlib import pyplot as plt  

img = cv2.imread("../img/lrn.jpg",1)
img_gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
'''
Sobel算子
Sobel算子函数原型如下：
dst = cv2.Sobel(src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]]) 
前四个是必须的参数：
第一个参数是需要处理的图像；
第二个参数是图像的深度，-1表示采用的是与原图像相同的深度。目标图像的深度必须大于等于原图像的深度；
dx和dy表示的是求导的阶数，0表示这个方向上没有求导，一般为0、1、2。
其后是可选的参数：
dst是目标图像；
ksize是Sobel算子的大小，必须为1、3、5、7。
scale是缩放导数的比例常数，默认情况下没有伸缩系数；
delta是一个可选的增量，将会加到最终的dst中，同样，默认情况下没有额外的值加到dst中；
borderType是判断图像边界的模式。这个参数默认值为cv2.BORDER_DEFAULT。
'''

img_sobel_x = cv2.Sobel(img_gray, cv2.CV_64F, 1, 0, ksize=3)  # 对x求导
img_sobel_y = cv2.Sobel(img_gray, cv2.CV_64F, 0, 1, ksize=3)  # 对y求导

# Laplace 算子  
img_laplace = cv2.Laplacian(img_gray, cv2.CV_64F, ksize=3)  

# Canny 算子  
img_canny = cv2.Canny(img_gray, 100 , 150)  

plt.subplot(231), plt.imshow(img_gray, "gray"), plt.title("Original"), plt.axis('off')
plt.subplot(232), plt.imshow(img_sobel_x, "gray"), plt.title("Sobel_x"), plt.axis('off')
plt.subplot(233), plt.imshow(img_sobel_y, "gray"), plt.title("Sobel_y"), plt.axis('off')
plt.subplot(234), plt.imshow(img_laplace,  "gray"), plt.title("Laplace"), plt.axis('off')
plt.subplot(235), plt.imshow(img_canny, "gray"), plt.title("Canny"), plt.axis('off')
plt.show()  

 效果展示：