【学习笔记】支配树
文章目录
- 0.概述
- 1.有关 d f s \rm dfs dfs 树
-
- 1.1.定义
- 1.2.性质
-
- 1.2.1.非树边
- 1.2.2. dfn \text{dfn} dfn 推论
- 2.有关支配树
-
- 2.1.半支配点与 s e m i semi semi
-
- 2.1.1.性质
- 2.1.2.求 s e m i semi semi
- 2.2.支配点
- 2.3.支配树
-
- 2.3.1.定义
- 2.3.2.存在性
- 2.3.3.建支配树
- 2.4.代码实现
- 3.例题
-
- 3.1.板题
- 4.后记
0.概述
用来求一张图中,从某个定点 s s s 出发,到达某一点 e e e 的路径上,必须经过哪些点。
这玩意儿有什么用呢?没什么用。 我只是个普及组选手啊
1.有关 d f s \rm dfs dfs 树
1.1.定义
在一个图中,以某一点为起点,进行深度优先遍历,将所有走过的边当作树边,形成的 树
。
注意:边可能是有向的。所以这并非一个传统意义上的树。
1.2.性质
记 dfn ( u ) \operatorname{dfn}(u) dfn(u) 为 u u u 是第几个被访问的(回溯不计入访问次数)。
1.2.1.非树边
在有向图中,对于任意非树边 ⟨ u , v ⟩ \langle u,v\rangle ⟨u,v⟩,要么 u u u 是 v v v 的祖先,要么 dfn ( u ) > dfn ( v ) \text{dfn}(u)>\text{dfn}(v) dfn(u)>dfn(v) 。
证明是轻松的。在 u u u 回溯时,对于所有已经访问的节点 x x x,要么 dfn ( x ) < dfn ( u ) \text{dfn}(x)<\text{dfn}(u) dfn(x)<dfn(u),要么 x x x 为 u u u 的子树内一点。而 v v v 都不满足,则此时必将 d f s \rm dfs dfs 到 v v v,进而 ( u , v ) (u,v) (u,v) 为树边,出现矛盾。
1.2.2. dfn \text{dfn} dfn 推论
对于任意两个点 u , v ( u ≠ v ) u,v\;(u\ne v) u,v(u=v),不妨设 dfn ( u ) < dfn ( v ) \text{dfn}(u)<\text{dfn}(v) dfn(u)<dfn(v),记 l c a ( u , v ) = x lca(u,v)=x lca(u,v)=x 。
- 对于 v v v 到 x x x 的树上路径中一点 y y y,一定有 dfn ( u ) < dfn ( y ) \text{dfn}(u)<\text{dfn}(y) dfn(u)<dfn(y) 。
- 对于 u u u 到 x x x 的树上路径中一点 y y y,一定有 dfn ( y ) < dfn ( v ) \text{dfn}(y)<\text{dfn}(v) dfn(y)<dfn(v) 。
其正确性是显然的;只需要画一张图就可以领会其中真谛了。用大白话来说就是,两个点的 d f n \rm dfn dfn 比较,在不超过 l c a lca lca 的位置都是一样的。
2.有关支配树
如果图是无向图,无向边转化为两条有向边。故以下内容均讨论有向图。
为了表述方便, u ⇒ v u\Rightarrow v u⇒v 表示 u u u 通过一条原图中存在的有向边 ⟨ u , v ⟩ \langle u,v\rangle ⟨u,v⟩ 到达 v v v,即二者直接相连。而 u → v u\rightarrow v u→v 表示 u ⇒ ⋯ ⇒ v u\Rightarrow \cdots \Rightarrow v u⇒⋯⇒v 或 u ⇒ v u\Rightarrow v u⇒v 。
2.1.半支配点与 s e m i semi semi
对于一个点 u u u,若存在一条路径 v → u ( v ≠ u ) v\rightarrow u\;(v\ne u) v→u(v=u),使得路径上除 u u u 和 v v v 的点 x x x 都满足 dfn ( x ) > dfn ( u ) \text{dfn}(x)>\text{dfn}(u) dfn(x)>dfn(u),则 v v v 为 u u u 的半支配点。
规定 s e m i ( x ) semi(x) semi(x) 为 x x x 的所有半支配点中 dfn \text{dfn} dfn 最小的一个。
2.1.1.性质
s e m i ( x ) semi(x) semi(x) 是 x x x 在 d f s \rm dfs dfs 树上的祖先。我尽量用简洁的方式证明它。
首先, x x x 的父节点是 x x x 的半支配点,故
dfn [ s e m i ( x ) ] ≤ dfn ( f a x ) < dfn ( x ) \text{dfn}[semi(x)]\le\text{dfn}(fa_x)<\text{dfn}(x) dfn[semi(x)]≤dfn(fax)<dfn(x)
这是比较核心的关系。有了这个,考虑 s e m i ( x ) → x semi(x)\rightarrow x semi(x)→x 路径上经过的第一个点 y y y(即路径为 s e m i ( x ) ⇒ y → x semi(x)\Rightarrow y\rightarrow x semi(x)⇒y→x,显然 y y y 是存在的,否则 s e m i ( x ) semi(x) semi(x) 已经是 x x x 的祖先),显然有 d f n ( y ) > d f n ( x ) {\rm dfn}(y)>{\rm dfn}(x) dfn(y)>dfn(x) 。
仔细思考一下, d f n ( y ) > d f n ( x ) > d f n [ s e m i ( x ) ] {\rm dfn}(y)>{\rm dfn}(x)>{\rm dfn}[semi(x)] dfn(y)>dfn(x)>dfn[semi(x)],那么 s e m i ( x ) ⇒ y semi(x)\Rightarrow y semi(x)⇒y 应当为祖先到儿子的边。即 s e m i ( x ) semi(x) semi(x) 是 y y y 的祖先。
根据 1.2.2.dfn推论, s e m i ( x ) semi(x) semi(x) 至少要达到 l c a ( x , y ) lca(x,y) lca(x,y) 才可以满足 d f n [ s e m i ( x ) ] < d f n ( x ) {\rm dfn}[semi(x)]<{\rm dfn}(x) dfn[semi(x)]<dfn(x),于是它就是 x x x 的祖先了。
2.1.2.求 s e m i semi semi
求 s e m i ( x ) semi(x) semi(x) 其实就是求半支配点。更新的时候,用 s e m i semi semi 更新(而非集合取并集)即可。
枚举 s e m i ( x ) → x semi(x)\rightarrow x semi(x)→x 中 x x x 的前驱 y y y,如果 d f n ( y ) < d f n ( x ) {\rm dfn}(y)<{\rm dfn}(x) dfn(y)<dfn(x),那就只能直接用 y y y 更新 s e m i ( x ) semi(x) semi(x) 了。否则,假设第一次走到 l c a ( x , y ) → y lca(x,y)\rightarrow y lca(x,y)→y 的点为 z z z,显然所有不到 l c a ( x , y ) lca(x,y) lca(x,y) 的 y y y 的祖先都可以作为 z z z,也都可以用 s e m i ( z ) semi(z) semi(z) 更新 s e m i ( x ) semi(x) semi(x) 。
形式化的,候选 s e m i semi semi 点的集合为 S x S_x Sx,那么有
S x = ⋃ ⟨ y , x ⟩ ⋃ z ∈ p a t h ( y , r o o t ) d f n ( z ) > d f n ( x ) S z S_x=\bigcup_{\langle y,x\rangle}\bigcup_{z\in path(y,root)}^{{\rm dfn}(z)>{\rm dfn}(x)}S_z Sx=⟨y,x⟩⋃z∈path(y,root)⋃dfn(z)>dfn(x)Sz
显然 S z S_z Sz 是合法的,因为 s e m i ( z ) semi(z) semi(z) 到 z z z 的路径上的点的 d f n > d f n ( z ) > d f n ( x ) {\rm dfn}>{\rm dfn}(z)>{\rm dfn}(x) dfn>dfn(z)>dfn(x) 。不过它是否有所遗漏呢?即 d f n \rm dfn dfn 介于 d f n ( x ) {\rm dfn}(x) dfn(x) 和 d f n ( z ) {\rm dfn}(z) dfn(z) 之间的点?
并没有呢。那些点想要走到 z z z,那就是让 d f n \rm dfn dfn 增加,那么这样的点必须是 z z z 的祖先。而 z z z 的祖先是不会先于 z z z 走到的!——比 l c a ( x , z ) lca(x,z) lca(x,z) 更深的,根据定义,不应该在 z z z 之前访问;比那更浅的,不能出现在路径上,因为其 d f n \rm dfn dfn 小于 d f n ( x ) {\rm dfn}(x) dfn(x) 了。
2.2.支配点
在一张图中设立一个源点 s s s 。
若对于某一点 e ( e ≠ s ) e\;(e\ne s) e(e=s) 满足所有从 s s s 到 e e e 的路径中都经过 u u u(即,在图中删去 u u u 之后,不存在 s s s 到 e e e 的路径),则称 u u u 为 e e e 的支配点,或 u u u 支配 e e e 。
显然一个点的支配点可能有很多个。一个生动形象的例子是链。
2.3.支配树
2.3.1.定义
对于一张图和其源点 s s s,支配树是满足该条件的树:
- 包含图中的每一个节点。
- 对于任意一点 u ( u ≠ s ) u\;(u\ne s) u(u=s),其祖先(包括 u u u 本身)均为其支配点。
- 对于任意一点 u ( u ≠ s ) u\;(u\ne s) u(u=s),其支配点均为其祖先(包括 u u u 本身)。
s s s 会是树的根节点。
2.3.2.存在性
我们要说明,为什么它会是一颗树?就像 S A M \tt SAM SAM 要说明,为什么存在合法的自动机状态转移。
先证明一个小结论:若 v v v 到 u u u 的每一条路径都经过 x x x,则存在一条从 x x x 到 u u u 的路径不含 v v v 。
证明很简单。用一点 C++ \text{C++} C++ 的想法。反证法,若不成立,其函数应该像这样:
void x_goto_u(){
x_goto_v(); // 由假设,必须先到达v
v_goto_u(); // 调用下面的函数
}
void v_goto_u(){
v_goto_x(); // 由假设,必须先到达x
x_goto_u(); // 调用上面的函数
}
这样就死递归了呀!而路径是客观存在的,所以归谬了。类似的,两个点互相支配也是不可能的。
现在,我们可以说明一些支配点之间的性质。若 u u u 有两个支配点 v v v 和 x x x,但是 v v v 和 x x x 没有支配关系(即支配关系非 “树形”),则存在两条从 s s s 到 u u u 的路径,一个是 s → v → u s\rightarrow v\rightarrow u s→v→u,另一个是 s → x → u s\rightarrow x\rightarrow u s→x→u 。
对于前者,令 s → v s\rightarrow v s→v 不经过 x x x(由于 v v v 和 x x x 没有支配关系,该路径必然存在)。为了使 x x x 支配 u u u,必须让 v → u v\rightarrow u v→u 总是经过 x x x 。根据上面的结论, x → u x\rightarrow u x→u 可以不经过 v v v,同理, s → x s\rightarrow x s→x 可以不经过 v v v,于是 s → x → u s\rightarrow x\rightarrow u s→x→u 完全不会经过 v v v,说明 v v v 不支配 u u u 啦,矛盾!
有了这一条,你会发现,一个点的所有支配点的导出子图是完全图。这个完全图又不能存在有向环(否则存在两个点互相支配,这是荒谬的),所以存在一个点被其他所有点支配。那么当前点就以这个点作为支配树上的父节点即可。
有点归纳法的感觉,对吗?对。按照 支配关系有向图
的拓扑序建树即可。
2.3.3.建支配树
据说又是 t a r j a n tarjan tarjan 发明的算法……
我们要 s e m i semi semi 有什么用? 去掉所有非树边,连边 ⟨ s e m i ( x ) , x ⟩ \langle semi(x),x\rangle ⟨semi(x),x⟩,支配关系不改变!
其实这个原因挺简单的。理解一下 s e m i semi semi 到底是什么:越过树边上的点。如果 u u u 是 v v v 的祖先,并且 u → v u\rightarrow v u→v,路径上 不需要 有 d f n < d f n ( v ) {\rm dfn}<{\rm dfn}(v) dfn<dfn(v) 的点——如果有,那其实还是 v v v 的祖先,没有飞越树上的点。
支配点肯定是 d f s \rm dfs dfs 树上的祖先(否则树边构成一条路径)。其树上祖先,如果不是支配点,只可能是被跨过了。而跨过就是 s e m i semi semi 嘛。如果感性的理解一下, s e m i semi semi 已经建好了所有桥,不需要更多的边了。
这样有什么好处呢?至少有一个:原图变为了 D A G DAG DAG!
其实 D A G DAG DAG 已经可以搞定了。对于所有前驱,求支配点交集,在支配树上体现为 l c a lca lca 的祖先。按照 d f n \rm dfn dfn 排序后,使用带权并查集,倍增维护 l c a lca lca 。时间复杂度 O ( n log n ) O(n\log n) O(nlogn) 。
可是人总是精益求精的。令 i d o m ( x ) idom(x) idom(x) 为 x x x 的支配点中 dfn \text{dfn} dfn 最大的点,寻找 i d o m ( x ) idom(x) idom(x) 的方法是:
记 P P P 为从 s e m i ( x ) semi(x) semi(x) 到 x x x 的树上路径点集(不包括 s e m i ( x ) semi(x) semi(x) 本身),找一个 z ∈ P z\in P z∈P 满足 dfn [ s e m i ( z ) ] \text{dfn}[semi(z)] dfn[semi(z)] 最小。
若 s e m i ( z ) = s e m i ( x ) semi(z)=semi(x) semi(z)=semi(x),则有 i d o m ( x ) = s e m i ( x ) idom(x)=semi(x) idom(x)=semi(x);否则有 i d o m ( x ) = i d o m ( z ) idom(x)=idom(z) idom(x)=idom(z) 。
对于前半句性感的证明就是,没有 s e m i ( x ) semi(x) semi(x) 的祖先连到 P P P 中的边,则删去 s e m i ( x ) semi(x) semi(x) , x x x 就不可达。毕竟 P P P 以内的所有点都连接 ⟨ s e m i ( p ) , p ⟩ \langle semi(p),p\rangle ⟨semi(p),p⟩ 之后也不能跨过 s e m i ( x ) semi(x) semi(x) 。别忘了 z z z 的定义哦!
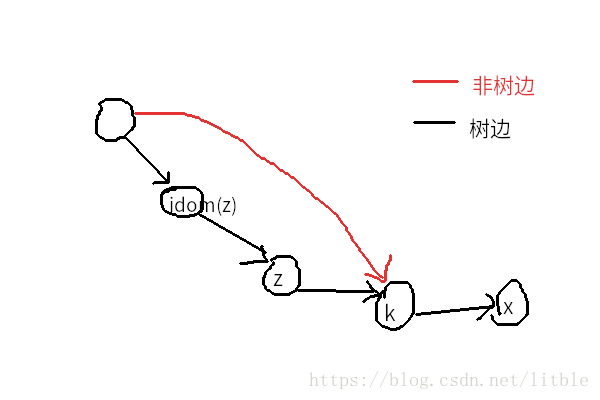
对于后半句性感的证明(见下图)就是:
假设删掉 i d o m ( z ) idom(z) idom(z) , x x x 依旧可达,则说明在 d f s dfs dfs 树上, i d o m ( z ) idom(z) idom(z) 有一个祖先,可以走一条非树边(也就是通过 s e m i semi semi 连出来的边,图中红边)到达 x x x 到 i d o m ( z ) idom(z) idom(z) 中间的一个点 k k k 。
若 z z z 不是 k k k 的祖先,则删掉 i d o m ( z ) idom(z) idom(z) 后 z z z 仍可达,与支配点定义不符,所以 z z z 是 k k k 的祖先。那么因为 z ∈ P z\in P z∈P ,所以 k ∈ P k\in P k∈P 。因为删除 i d o m ( z ) idom(z) idom(z) 后 s e m i ( z ) semi(z) semi(z) 不可达,所以 dfn [ s e m i ( k ) ] < dfn [ i d o m ( z ) ] < dfn [ s e m i ( z ) ] \text{dfn}[semi(k)]<\text{dfn}[idom(z)]<\text{dfn}[semi(z)] dfn[semi(k)]<dfn[idom(z)]<dfn[semi(z)],与 z z z 的定义矛盾,所以该假设不可能成立。
版权声明:本文为CSDN博主「litble」的原创文章,遵循CC 4.0 by-sa版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/litble/article/details/83019578
这一小节是摘录的,进行了部分修改。
2.4.代码实现
我们要 i d o m idom idom 来干嘛呢?在支配树上, x x x 的父亲就是 i d o m ( x ) idom(x) idom(x) 呗。
发现 s e m i semi semi 需要用到 dfn \text{dfn} dfn 值更大的点的 s e m i semi semi 。那就按照 dfn \text{dfn} dfn 从大到小处理。
用 带权并查集 好像可以做。用 m i ( x ) mi(x) mi(x) 存该点到根节点的路径中, dfn [ s e m i ( z ) ] \text{dfn}[semi(z)] dfn[semi(z)] 值最小的一个 z z z 。毕竟也就用 y y y 的祖先中比 x x x 的 dfn \text{dfn} dfn 大的点呗!
求 i d o m idom idom 该怎么办呢?它要用到 s e m i ( x ) semi(x) semi(x) 与 x x x 之间的信息。那就等到 s e m i ( x ) semi(x) semi(x) 处理完的时候处理吧!——那个时候,中间的所有点都处理了。
很巧的是,恰好此时 s e m i ( x ) semi(x) semi(x) 的祖先还没处理!可以一并使用并查集,因为根节点就是 s e m i ( x ) semi(x) semi(x) 。
3.例题
3.1.板题
传送门 to HDU
#include4.后记
再次鸣谢:litble的感性理解支配树,提供了思路与代码!
支配树为作者自学,如有错误之处,还请大佬斧正!