最小生成树算法(Prim Kruskal)
目录
- 最小生成树算法总览
- 最小生成树的定义及性质
- Prim(普利姆)算法
-
- 1.朴素Prim算法
-
- 算法步骤
- 2.堆优化Prim算法
-
- 算法步骤
- 3.算法运用
-
- Prim算法求最小生成树
-
- 流程实现
- 朴素Prim的代码实现
- 堆优化Prim的代码实现
- Kruskal(克鲁斯卡尔)算法
-
- 1.算法步骤
- 2.算法运用
-
- Kruskal算法求最小生成树
最小生成树算法总览
最小生成树的定义及性质
最小生成树(Minimum Spanning Tree,简称MST)是图论中的一个概念。给定一个连通的无向图,最小生成树是指包含图中所有顶点的一棵树,且该树的所有边的权重之和最小。
最小生成树的基本定义和性质:
- 连通性:最小生成树必须包含图中的所有顶点,并且通过边将它们连接起来,确保整个图是连通的,即任意两个顶点之间都有路径。(一颗有 n 个顶点的生成树有且仅有 n−1 条边,如果生成树中再添加一条边,则必定成环。)
- 无环:最小生成树是一棵树,所以不能包含任何环(即回路)。
- 最小权重:最小生成树的边权重之和应当尽可能地小。在有多个满足条件的最小生成树时,它们的权重之和是相同的。
实际的场景:
最小生成树在现实生活和计算机科学中有广泛的实际运用场景。以下是一些常见的应用场景:
-
网络设计与通信:在通信网络、电信和计算机网络的设计中,最小生成树用于确定连接所有节点的最优路径,以确保数据传输的高效性和稳定性。
-
电力传输:在电力系统中,最小生成树可用于确定电力线路的布置,确保所有地区都能得到电力供应,同时最小化电力线路的长度和损耗。
-
交通规划:在城市交通规划中,最小生成树可以用来规划公交线路或道路网络,以实现最短路径和最小交通拥堵。
-
管道布置:在石油、天然气等管道网络的布置中,最小生成树可用于确定最优的管道布置,以最小化材料和成本的使用。
-
无线传感器网络:在无线传感器网络中,传感器节点需要有效地传输数据到基站,通过最小生成树可以构建出最优的通信路径,延长网络寿命。
-
图像分割:在计算机视觉领域,图像分割问题可以转化为最小生成树问题,用于将图像分成连通的区域,有助于图像处理和分析。
-
电路板设计:在电路板布线时,最小生成树可用于确定元件之间的最优连接方式,以最小化电路的面积和布线的复杂性。
-
聚类分析:在数据挖掘和机器学习中,最小生成树可以用于聚类分析,将相似的数据点连接在一起形成簇。
Prim(普利姆)算法
1.朴素Prim算法
朴素Prim算法(Naive Prim Algorithm),也称为简单Prim算法,是用于求解无向图的最小生成树的一种基本而直观的算法。该算法是以其发明者之一、计算机科学家Jarník的名字来命名的,也被称为Jarník算法。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
算法步骤
- 选择一个起始节点作为最小生成树的起点。
- 将该起始节点加入最小生成树集合,并将其标记为已访问。
- 在所有与最小生成树集合相邻的边中,选择权重最小的边和它连接的未访问节点。
- 将该边和节点加入最小生成树集合,并将该节点标记为已访问。
- 重复步骤3和步骤4,直到最小生成树集合包含了图中的所有节点。
2.堆优化Prim算法
时间复杂度: O ( m log n ) O(m \log n) O(mlogn)
算法步骤
- 初始化 d i s t dist dist 数组为 I N F INF INF,表示所有节点到集合的距离为无穷大。
- 创建一个小根堆,堆中的元素为( d i s t dist dist 值, 节点编号)。
- 堆中先插入 ( 0 , 1 ) (0, 1) (0,1) 表示节点1进入集合, d i s t dist dist 值为 0 0 0。
- 每次从堆中取出 d i s t dist dist 值最小的元素 ( d , u ) (d, u) (d,u),将u加入集合。
- 对 u u u 相邻的所有节点 v v v,更新 d i s t [ v ] = m i n ( d i s t [ v ] , g [ u ] [ v ] ) dist[v] = min(dist[v], g[u][v]) dist[v]=min(dist[v],g[u][v]),并更新堆中的相应元素。
- 重复步骤 4 、 5 4、5 4、5,直到所有节点都加入集合。
- 最后根据取出的 d i s t dist dist 值之和求得最小生成树权重。
3.算法运用
Prim算法求最小生成树
题目描述:
给定一个 n n n 个点 m m m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 i m p o s s i b l e impossible impossible。
给定一张边带权的无向图 G = ( V , E ) G=(V,E) G=(V,E),其中 V V V 表示图中点的集合, E E E 表示图中边的集合, n = ∣ V ∣ n=|V| n=∣V∣, m = ∣ E ∣ m=|E| m=∣E∣。
由 V V V 中的全部 n n n 个顶点和 E E E 中 n − 1 n−1 n−1 条边构成的无向连通子图被称为 G G G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G G G 的最小生成树。
输入格式:
第一行包含两个整数 n n n 和 m m m。
接下来 m m m 行,每行包含三个整数 u , v , w u,v,w u,v,w,表示点 u u u 和点 v v v 之间存在一条权值为 w w w 的边。
输出格式:
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围:
1 ≤ n ≤ 500 , 1 ≤ m ≤ 1 0 5 1≤n≤500,1≤m≤10^5 1≤n≤500,1≤m≤105,图中涉及边的边权的绝对值均不超过 10000 10000 10000。
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例:
6
流程实现
我们将图中各个节点用数字 1 ∼ n 1∼n 1∼n 编号。

要将所有景点连通起来,并且边长之和最小,步骤如下:
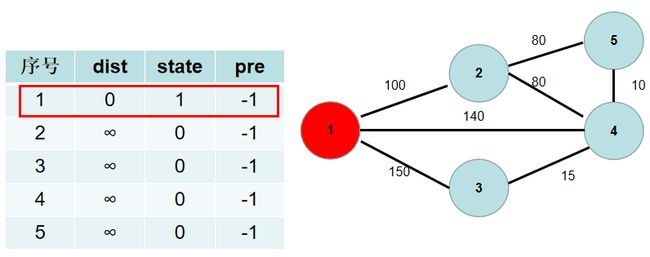
①用一个 s t st st 数组表示节点是否已经连通。 s t [ i ] st[i] st[i] 为真,表示已经连通, s t [ i ] st[i] st[i] 为假,表示还没有连通。初始时, s t st st 各个元素为假。即所有点还没有连通。用一个 d i s t dist dist 数组保存各个点到连通部分的最短距离, d i s t [ i ] dist[i] dist[i] 表示 i 节点到连通部分的最短距离。初始时, d i s t dist dist 数组的各个元素为无穷大。用一个 pre 数组保存节点的是和谁连通的。 p r e [ i ] = k pre[i]=k pre[i]=k 表示节点 i i i 和节点 k k k 之间需要有一条边。初始时, p r e pre pre 的各个元素置为 −1。
②从 1 1 1 号节点开始扩充连通的部分, 1 1 1 号节点与连通部分的最短距离为 0 0 0,即 d i s t [ i ] dist[i] dist[i] 值为 0 0 0。
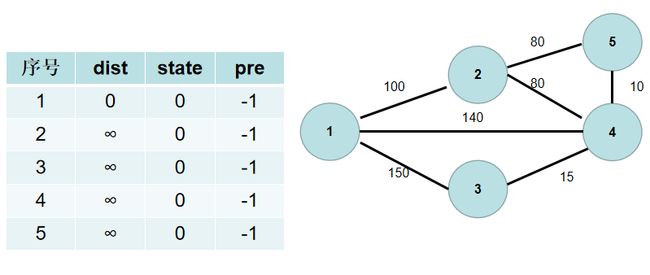
③遍历 d i s t dist dist 数组,找到一个还没有连通起来,但是距离连通部分最近的点,假设该节点的编号是 t t t。 t t t 节点就是下一个应该加入连通部分的节点, s t [ t ] st[t] st[t] 置为 t r u e true true。用青色点表示还没有连通起来的点,红色点表示连通起来的点。这里青色点中距离最小是 d i s t [ 1 ] dist[1] dist[1],因此 s t [ 1 ] st[1] st[1] 置为 t r u e true true。
④遍历所有与 t t t 相连但没有加入到连通部分的点 j j j,如果 j j j 距离连通部分的距离大于 t ∼ j t∼j t∼j 之间的距离,即 d i s t [ j ] > g [ t ] [ j ] dist[j]>g[t][j] dist[j]>g[t][j]( g [ t ] [ j ] g[t][j] g[t][j] 为 t ∼ j t∼j t∼j 节点之间的距离),则更新 d i s t [ j ] dist[j] dist[j] 为 g [ t ] [ j ] g[t][j] g[t][j]。这时候表示, j j j 到连通部分的最短方式是和 t t t 相连,因此更新 p r e [ j ] = t pre[j]=t pre[j]=t。
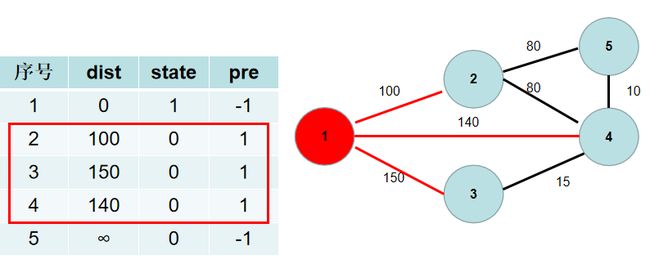
与节点 1 1 1 相连的有 2 , 3 , 4 2, 3, 4 2,3,4 号节点。 1 − > 2 1−>2 1−>2 的距离为 100 100 100,小于 d i s t [ 2 ] dist[2] dist[2], d i s t [ 2 ] dist[2] dist[2] 更新为 100 100 100, p r e [ 2 ] pre[2] pre[2] 更新为 1 1 1。 1 − > 4 1−>4 1−>4 的距离为 140 140 140,小于 d i s t [ 4 ] dist[4] dist[4], d i s t [ 4 ] dist[4] dist[4]更新为 140 140 140, p r e [ 4 ] pre[4] pre[4] 更新为 1 1 1。 1 − > 3 1−>3 1−>3 的距离为 150 150 150,小于 d i s t [ 3 ] dist[3] dist[3], d i s t [ 3 ] dist[3] dist[3] 更新为 150 150 150, p r e [ 3 ] pre[3] pre[3] 更新为 1 1 1。
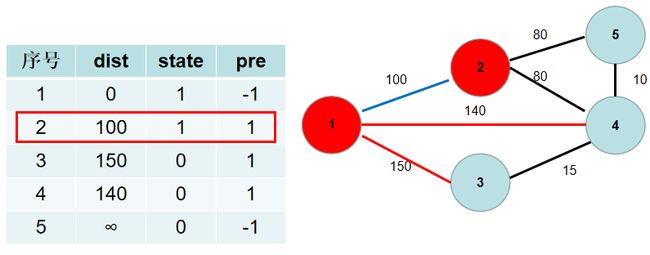
重复 3 − 4 3-4 3−4 步骤,直到所有节点的状态都被置为 1 1 1。这里青色点中距离最小的是 d i s t [ 2 ] dist[2] dist[2],因此 s t [ 2 ] st[2] st[2] 置为 1 1 1。
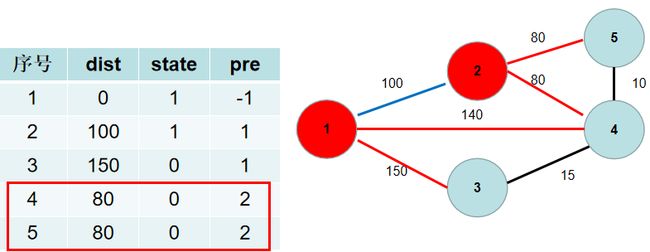
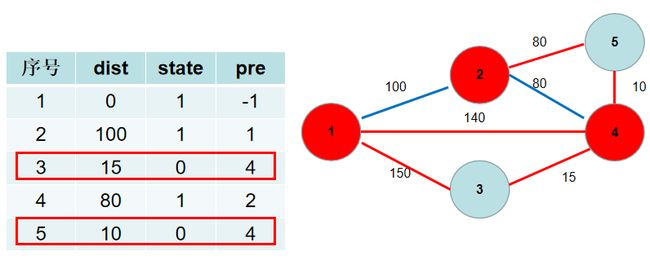
与节点 2 2 2 相连的有 5 5 5, 4 4 4号节点。 2 − > 5 2−>5 2−>5 的距离为 80 80 80,小于 d i s t [ 5 ] dist[5] dist[5],dist[5] 更新为 80 80 80, p r e [ 5 ] pre[5] pre[5] 更新为 2 2 2。 2 − > 4 2−>4 2−>4 的距离为 80 80 80,小于 d i s t [ 4 ] dist[4] dist[4], d i s t [ 4 ] dist[4] dist[4] 更新为 80 80 80, p r e [ 4 ] pre[4] pre[4] 更新为 2 2 2。
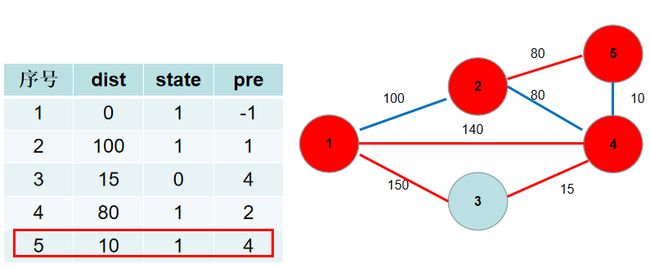
选 d i s t [ 4 ] dist[4] dist[4],更新 d i s t [ 3 ] dist[3] dist[3], d i s t [ 5 ] dist[5] dist[5], p r e [ 3 ] pre[3] pre[3], p r e [ 5 ] pre[5] pre[5]。
选 d i s t [ 5 ] dist[5] dist[5],没有可更新的。
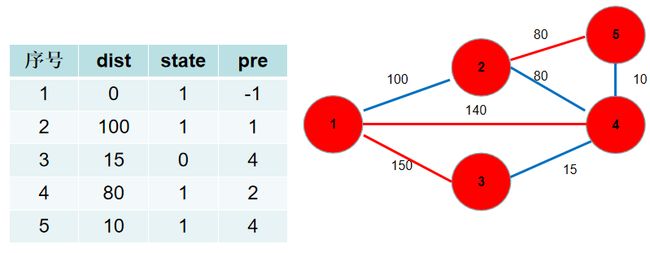
选 d i s t [ 3 ] dist[3] dist[3],没有可更新的。

6.此时 d i s t dist dist 数组中保存了各个节点需要修的路长,加起来就是。 p r e pre pre 数组中保存了需要选择的边。
朴素Prim的代码实现
#define _CRT_SECURE_NO_WARNINGS
#include注意:
累加记得提前,防止负权自环。
- 与
Dijkstra可迭代 n − 1 n-1 n−1 次不同,Prim需要迭代 n n n 次。 - 最小生成树是针对无向图的,所以在读入边的时候,需要赋值两次。
- 要先累加再更新,避免 t t t 有自环,影响答案的正确性。后更新不会影响后面的结果么?不会的,因为 d i s t [ i ] dist[i] dist[i] 为 i i i 到集合 S S S 的距离,当 t t t 放入集合后,其 d i s t [ t ] dist[t] dist[t] 就已经没有意义了,再更新也不会影响答案的正确性。
- 需要特判一下第一次迭代,在我们没有做特殊处理时,第一次迭代中所有点到集合S的距离必然为无穷大,而且不会进行更新(也没有必要),所以不需要将这条边(第一次迭代时,找到的距离集合 S S S 最短的边)累加到答案中,也不能认定为图不连通。
- 如果需要设置起点为 i i i 的话,在初始化 d i s t dist dist 数组之后, d i s t [ i ] = 0 dist[i] = 0 dist[i]=0 即可,这样也可以省去每轮迭代中的两个 i f if if 判断。
附加:
带路径输出的Prim算法
#define _CRT_SECURE_NO_WARNINGS
#include堆优化Prim的代码实现
#define _CRT_SECURE_NO_WARNINGS
#includeKruskal(克鲁斯卡尔)算法
Kruskal算法是计算无向连通加权图的最小生成树的经典贪心算法。
时间复杂度: O ( m log m ) O(m \log m) O(mlogm)
1.算法步骤
- 创建一个空的最小生成树 T T T。
- 将图中的所有边按权重从小到大排序。【 O ( m log m ) O(m \log m) O(mlogm) Kruskal算法时间复杂度的瓶颈】
- 从权重最小的边开始,如果当前边连接的两个节点不在 T T T 中,则将当前边加入 T T T,否则跳过当前边。【 O ( m ) O(m) O(m)】
- 重复步骤 3 3 3,直到T包含图中的所有节点为止。
- 最后得到的 T T T 即为该图的最小生成树。
2.算法运用
Kruskal算法求最小生成树
题目描述:
给定一个 n n n 个点 m m m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G = ( V , E ) G=(V,E) G=(V,E),其中 V V V 表示图中点的集合, E E E 表示图中边的集合, n = ∣ V ∣ n=|V| n=∣V∣, m = ∣ E ∣ m=|E| m=∣E∣。
由 V V V 中的全部 n n n 个顶点和 E E E 中 n − 1 n−1 n−1 条边构成的无向连通子图被称为 G G G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G G G 的最小生成树。
输入格式:
第一行包含两个整数 n n n 和 m m m。
接下来 m m m 行,每行包含三个整数 u , v , w u,v,w u,v,w,表示点 u u u 和点 v v v 之间存在一条权值为 w w w 的边。
输出格式:
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围:
1 ≤ n ≤ 1 0 5 , 1 ≤ m ≤ 2 ∗ 1 0 5 1≤n≤10^5,1≤m≤2*10^5 1≤n≤105,1≤m≤2∗105,图中涉及边的边权的绝对值均不超过 1000 1000 1000。
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例:
6
代码实现:
#define _CRT_SECURE_NO_WARNINGS
#include