蓝桥杯上岸必背！！！(并查集补更)

蓝桥杯上岸必背！！！(并查集补更)

大家好 我是寸铁

冲刺蓝桥杯省一模板大全来啦

蓝桥杯4月8号就要开始了

距离蓝桥杯省赛倒数第3天 ❗️ ❗️ ❗️

还没背熟模板的伙伴们背起来

真题千千万万遍，蓝桥省一自然现！ ✌️

日更3000里，蓝桥眷顾你

暴力出奇迹，打表过样例

祝大家4月8号蓝桥杯上岸 ☀️

不清楚蓝桥杯考什么的点点下方

考点秘籍

想背纯享模版的伙伴们点点下方

蓝桥杯省一你一定不能错过的模板大全(第一期)

蓝桥杯省一你一定不能错过的模板大全（第二期）

蓝桥杯省一你一定不能错过的模板大全（第三期）

蓝桥杯省一你一定不能错过的模板大全（第四期）！！！

想背注释模版的伙伴们点点下方

蓝桥杯必背第一期

蓝桥杯必背第二期

往期精彩回顾

蓝桥杯上岸每日N题 第一期(一)！！！

蓝桥杯上岸每日N题第一期(二)！！！

蓝桥杯上岸每日N题第一期(三)！！！

蓝桥杯上岸每日N题第二期(一)！！！

蓝桥杯上岸每日N题第三期(一)！！！

蓝桥杯上岸每日N题 第四期(最少刷题数)！！！

蓝桥杯上岸每日N题 第五期(山)！！！

蓝桥杯上岸每日N题 第六期(求阶乘)！！！

操作系统期末题库 第九期(完结)

LeetCode Hot100 刷题(第三期)

idea创建SpringBoot项目报错解决方案

数据库SQL语句（期末冲刺）

想看JavaB组填空题的伙伴们点点下方

填空题

竞赛干货

算法竞赛字符串常用操作大全

蓝桥杯上岸必刷！！！(模拟/枚举专题)

蓝桥杯上岸必背！！！ (第三期 DP)

蓝桥杯上岸必背！！！(第四期DFS)

蓝桥杯上岸必背！！！(第五期BFS)

蓝桥杯上岸必背！！！(第六期树与图的遍历)

蓝桥杯上岸必背！！！(第七期 最短路算法)

蓝桥杯上岸必背！！！(第八期 简单数论)

---

前言

喜欢的小伙伴可以关注我，关注寸铁，我们一起上岸4.8蓝桥杯！！！

并查集

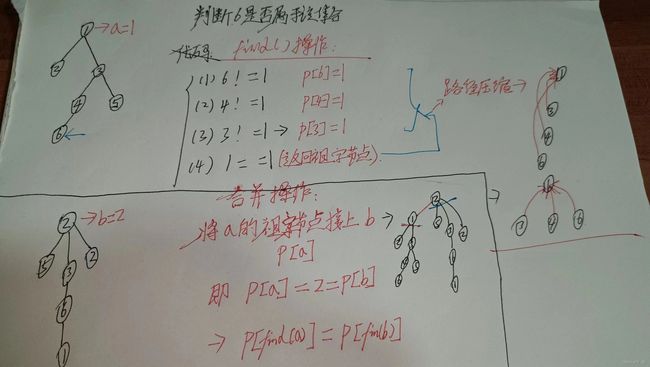
合并集合

基本思想：
每个集合用一颗树来表示，树根的编号就是整个集合的编号。
每个节点存储它的父节点，p[x]表示x的父节点。
#三个问题
P1：如何判断树根
if(p[x]==x)即根节点和输入的集合编号(它本身)相等

P2:如何求x的集合编号
if(p[x]==x) return p[x];

P3：如何合并两个集合
p[x]是x的集合编号，p[y]是y的集合编号
那么，需要让p[x]接上y，即x的祖宗节点为y的一个子节点。

返回祖宗节点：

return p[x];
如果p[x]等于x的话，就返回p[x]即根节点x，此时的返回值为常量x。

路径压缩:

if(p[x]!=x)p[x]=find(p[x]);
代码解读：
如果p[x]不等于x的话，就进行路径压缩操作，即让每个p[x]与自身进行比较，很明显相等，返回的均是x，这样就实现了路径压缩。

分析过程图

#代码

import java.util.*;
public class Main{
    static int N=100010;
    static int p[]=new int[N];
    public static int find(int x){//返回祖宗节点+路径压缩
        //条件：节点的父节点p[x]为x(祖宗节点)
        //换句话来说，即只有祖宗节点等于它本身x
        if(p[x]!=x)p[x]=find(p[x]);//路径压缩
        
        return p[x];//返回祖宗节点
    }
   
    //等同于如下代码：
    public static int  find (int x){
        if(p[x]==x)return x;
        else{
            p[x]=find p[x];
        }
        return p[x];
    }
    
    public static void main(String []args){
        Scanner in = new Scanner(System.in);
        int n=in.nextInt();
        int m=in.nextInt();
        //初始化：即让当前数据的父节点指向其本身，将父节点设置为自己。
        for(int i=1;i<=n;i++)p[i]=i;
        while(m-->0){
            String s=in.next();
            int a=in.nextInt();
            int b=in.nextInt();
            //合并，将a的祖宗节点作为b的一个子节点插入
            if(s.equals("M"))p[find(a)]=find(b);
            else{//查找b和a的集合编号是否一致
                if(find(b)==find(a)){
                    System.out.println("Yes");
                }
                else{
                    System.out.println("No");
                }
            }
        }
    }
}

#参考资源
https://b23.tv/UDjPN9Y
https://b23.tv/13OXh8I

连通块中点的数量

思路

判断两节点是否在同一连通块中,就是看他们的祖宗节点是否相同。
合并操作使用并查集，将两个连通块合并成一个连通块。
还需要多维护一个size[]数组，用于统计节点所在连通块的数目。
我们在求解某个点在连通块中的数量时，由于是连通块，一个点所在的块的点都会被包含在内,我们可以直接找到他的祖宗节点，用祖宗节点记录块中点的个数，再返回他的祖宗节点的个数即可。

注意

size[find(b)]+=size[find(a)];
p[find(a)]=find(b);
顺序是先加后合并，先合并后加可能会造成结果出错！
注：这里的a、b顺序需要反着写
就比如size[]中是find(b)、find(a)
p[]中是find(a)、find(b)
解释：我们在将a的祖宗节点指向b的祖宗节点时，是将a合并到b中。
所以，size数量时，应该是b的数量合并a的数量。
反之，也成立。
不清楚的同学可以看这篇题解：
https://www.acwing.com/activity/content/code/content/5333512/

ACcode

import java.util.*;
public class Main{
    static int N=100010;
    static int size[]=new int[N];
    static int p[]=new int[N];
    public static int find(int x){
        if(p[x]!=x)p[x]=find(p[x]);
        return p[x];
    }
    public static void main(String []args){
        Scanner in = new Scanner(System.in);
        int n=in.nextInt();
        int m=in.nextInt();
        for(int i=1;i<=n;i++){
        
            size[i]=1;
            //初始时自己也算做一个点
            //多维护一个size[]数组，用于记录点的个数。
            p[i]=i;
        }
        while(m-->0){
            String s=in.next();
          if(s.equals("C")){
              int a=in.nextInt();
              int b=in.nextInt();
              if(find(a)!=find(b)){
              //合并两个节点
                  size[find(b)]+=size[find(a)];
            //b的祖宗节点点数加上a的祖宗节点个数
                  p[find(a)]=find(b);
            //a的祖宗节点为b的祖宗节点，合并成一个连通块
          
              }
          }
            else if(s.equals("Q1")){
                int a=in.nextInt();
                int b=in.nextInt();
                if(find(a)==find(b))System.out.println("Yes");
                else System.out.println("No");
            }
            else if(s.equals("Q2")){
                int a=in.nextInt();
                System.out.println(size[find(a)]);
            }
        }
    }
}

食物链

核心思想：

运用并查集，去维护每一个点到根节点的距离，根据同余定理，判断两个点(动物)的关系。
除了维护p[]数组，还需额外维护d[]数组去计算点到根节点的距离，再根据各个点到根节点距离差%3的余数来确定两个点的关系。

余数关系：

余数为1，表示吃根节点。
余数为2，表示可以被根节点吃。
余数为0，表示和根节点是同类。

可以进一步引申出x吃y,则x到根节点的距离比y到根节点的距离多1

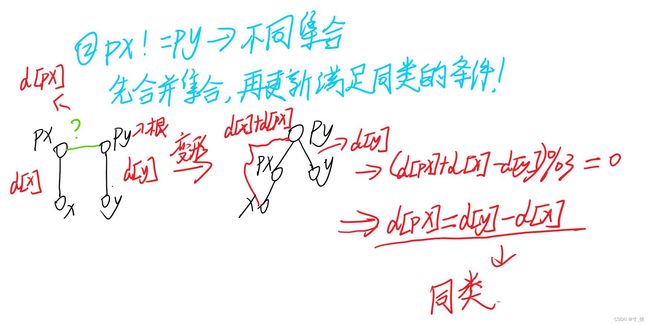
分析图

理解题意

find()方法

询问t为1(x、y同类)

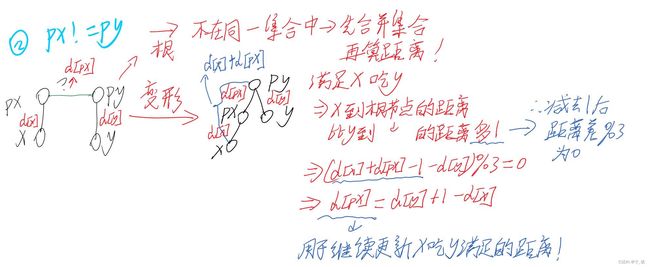
询问t为2（x吃y)

代码

import java.util.*;
import java.io.*;
public class Main{
	static int N=50010;
	static int n,m;
	static int []p=new int[N];
	static int []d=new int[N];	
	public static int find(int x) {
		if(p[x]!=x) {
			int t = find(p[x]);//记录根节点
			d[x]+=d[p[x]];//计算x到根节点的距离
			p[x]=t;//x的父节点直接指向根节点
			
		}
		return p[x];
		
	}
	
	public static void main(String []args) throws IOException {
	BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
		String []str=in.readLine().split(" ");
		 n=Integer.parseInt(str[0]);
		 m=Integer.parseInt(str[1]);
		for(int i=0;i<n;i++) {
			p[i]=i;//初始化每个点
		}
		int res=0;//假话个数
		
		while(m-->0) {
			String []strs=in.readLine().split(" ");
			int t = Integer.parseInt(strs[0]);
			int x = Integer.parseInt(strs[1]);
			int y=Integer.parseInt(strs[2]);
			
			if(x>n||y>n)res++;// >n表示假话
			
			else {//均在1-n这个集合内
				int px=find(x),py=find(y);//先找到x、y的父节点
				//询问是1，同类关系
				if(t==1) {
					//在同一集合内
					if(px==py&&(d[x]-d[y])%3!=0)res++;//不是同类，为假话
					//不在同一集合内
					else if(px!=py) {
						p[px]=py;//先合并两个集合
						//距离相等，为同类
						d[px]=d[y]-d[x];
					}
					
				}
				//询问是2，吃的关系
				else {
				    //在同一集合内，不满足x吃y的关系，即距离差%3不为0
					if(px==py&&(d[x]-d[y]-1)%3!=0)res++;
					//不在同一集合内
					else if(px!=py)
					{
					     p[px]=py;//先合并两个集合
						//p[px]=p[y];
						//满足吃的关系，更新d[px]
						d[px]=d[y]+1-d[x];
					}
				}
			}
		}
		System.out.println(res);
	}
}

亲戚

公共祖先(亲戚):并查集

分析

判断两个人是不是亲戚，直接判断他们的祖宗是不是同一个人即可。
判断公共祖宗/祖先，用并查集即可
运行时间:4458 ms
没有快读快写,会暴 TLE，只能过8个案例。

快读快写后,可以AC,通过全部案例。
注意：flush()放置在整个while循环之外,不然每一次循环就flush()刷新，需要耗费k倍的刷新时间导致TLE,只需要刷新一次即可。

不清楚并查集的同学可以看这篇题解：
https://www.acwing.com/activity/content/code/content/5321411/

import java.io.*;
public class Main{
	static int N=20010;
	static int p[]=new int[N];
	public static int find(int x) {
		if(p[x]!=x)p[x]=find(p[x]);
		return p[x];
	}
	public static void main(String []args)throws IOException {
		BufferedReader re=new BufferedReader(new InputStreamReader(System.in));
		PrintWriter pw=new PrintWriter(new OutputStreamWriter(System.out));
		String str[]=re.readLine().split(" ");
		int n=Integer.parseInt(str[0]);
		int m=Integer.parseInt(str[1]);
		for(int i=1;i<=n;i++) {
			p[i]=i;
		}
		while(m-->0) {
		    String s[]=re.readLine().split(" ");
			int a=Integer.parseInt(s[0]);
			int b=Integer.parseInt(s[1]);
			if(find(a)!=find(b))p[find(a)]=find(b);
		}
		String s1[]=re.readLine().split(" ");
		int k=Integer.parseInt(s1[0]);
		while(k-->0) {
		    String s2[]=re.readLine().split(" ");
			int q1=Integer.parseInt(s2[0]);
			int q2=Integer.parseInt(s2[1]);
			if(find(q1)==find(q2)) {
				pw.println("Yes");
			}
			else {
				pw.println("No");
			}
		}
		pw.flush();//刷新流的位置放在整个while循环外
	}
}

✨ ✨ ✨
看到这里，不妨点个关注