机器学习-随笔（待续）

环境配置

安装python（略）

Anaconda

Anaconda下载网址：Anaconda | The World’s Most Popular Data Science Platform

相关安装配置教程：Anaconda软件安装流程 - 知乎 (zhihu.com)

配置完成后需要将该环境配置到Pycharm中，具体配置步骤较为简单，CSDN一下

Pytorch

Pytorch下载网址：Start Locally | PyTorch

Pytorch下载建议使用Anaconda的conda指令进行安装下载

使用conda进行安装，自行选择CUDA的版本（Compute Platform），注意这里的版本要与自己电脑显卡的CUDA驱动程序版本对应，具体各版本对应关系可以到网上进行查阅。如N卡可以在NVIDIA控制面板查看到如下信息（图中驱动程序版本 527.37）

版本要严格对应，否则会导致无法使用GPU进行训练。Pytorch占用空间比较大，使用conda命令进行Pytorch可能会出现下载失败的情况，建议多尝试几次，或者换个较好的网络环境。

安装好后在Pycharm创建项目并输入如下代码进行验证Pytorch是否安装成功并且可用

import torch
    
A = torch.ones([1, 2])
B = torch.ones([1, 2])
print(A * B)
# 结果：tensor([[1., 1.]])

#测试GPU是否可用：

import torch
    
A = torch.ones([1, 2]).cuda()
B = torch.ones([1, 2]).cuda()
print(A * B)
#  结果同上，不报错即GPU可用

相关库

有些库pytorch中已经带有

1. matplotlib（画图）

2.pandas（csv、xls、xlsx表格读取）

3.PIL（图片读取）

4.torchvision（图像和张量进行转换）

神经网络基础

注：以下所有代码举例均使用pytorch

Pytorch官方文档：PyTorch documentation — PyTorch 1.13 documentation

1. 张量

在Pytorch中张量是tensor，类似于numpy，可以理解为一个list或是数学意义上的矩阵。Pytorch的所有运算全都离不开张量。即使是图像和文字在进入网络前都需要转换成张量。张量配有一系列方法，如where、ones、zeros、reshape、unsqueeze等，学好相关方法可以提高神经网络训练效率。

同list一样，张量支持切片操作

1.1. shape

每一个张量都有一个shape，因为在神经网络中通常都是四维甚至更高维度的数据，无法通过print来进行直观地观察。因此需要一个属性来显示张量的形状。使用方法：t.shape

t = torch.ones([1,2])
print(t.shape)
# 结果：torch.Size([1, 2]) 可以理解为一个1行两列的 “二维数组”

1.2. torch.ones(shape)

可以生成所有值为1的张量

t = torch.ones([1,2])   #最终生成shape为[1,2]的张量

1.3. torch.zeros(shape)

使用方法同torch.ones()，最终生成的张量值为0

1.4. torch.rand(shape)

使用方法同torch.rand()，最终生成[0,1]的随机数张量

1.5. cuda()

张量调用cuda()方法及代表将当前张量存储到显存中，后续的张量运算都会在GPU中计算

注意：两个不同设备的张量不能计算，如一个张量声明了cuda()但另一个张量在cpu中，会报错

t = torch.ones([1,2])
t = t.cuda()

1.6. cpu()

同cuda()，将当前张量从显存移入内存，使用CPU计算

1.7. torch.where()

本方法通常用在对张量进行条件筛选上，如：要筛选张量中所有值大于0.3的元素并置为1，其余置为0，如果对于有几十万个元素的张量(一张500*500像素的RGB图像对应的张量元素数量为75万)来说，鉴于python的解释机制，for循环需要100ms左右（不同配置有所不同）。而torch.where()实现相同功能只需要2ms左右（CPU）

t = torch.ones([3,500,500])
result = torch.where(t>.3,torch.ones(t.shape),torch.zeros(t.shape))
# where中三个参数可以类比三目元，第一个参数是条件，如果条件成立则将当前位置的元素置为第二个元素对应位置的数值，否则置为第三个元素对应位置的数值
    
#注意 torch.where()中的两个参数输入的张量的设备需要与条件表达式中的张量设备相同  设备即CPU或GPU

1.8. torch.unsqueeze(tensor,dim)

用于扩充维度，能够将目标张量的某一维度（dim）前面扩充一个维度

t = torch.ones([3, 500, 500])
t = torch.unsqueeze(t, dim=1)
print(t.shape)
# torch.Size([3, 1, 500, 500])

1.9. torch.reshape(tensor,shape)

用于改变张量的shape

t = torch.ones([3, 500, 500])
t=torch.reshape(t,[-1,10,100])
print(t.shape)
# torch.Size([750, 10, 100])

1.10. torch.save()

用于保存模型、优化器的参数，以便后续对训练好的模型或者正在训练的模型进行配置恢复原状。

Net = ModelName()
torch.save(Net.state_dict(), './modelpath.pth')

1.11. torch.load()

用于加载模型、优化器参数。

Net = ModelName()
Net.load_state_dict(torch.load('./modelpath.pth'))

1.12. eval()

禁掉BN层和Dropout层，通常在预测或验证模型时使用。

Net = ModelName()
Net.eval()

注意：eval()对于采用BN层的神经网络来说，在进行预测的时候是必须的，否则会严重干扰预测结果的准确性。

1.13. torch.mean()

求一个张量（或指定维度）的均值

t = torch.ones([2,3,4])
m = torch.mean(t,dim=0)        #dim不填时，默认为求整个张量的均值，否则为求某一维度的均值

1.14. torch.sum()

求和，与torch.mean()用法相同

1.15. torch.max()

与torch.mean()用法相同，求整个张量（或指定维度）的最大值。同理，有torch.min()

1.16. torch.argmax()

与torch.mean()用法相同，但通常不会不指定dim单独使用argmax()，目的是返回指定维度的最大值索引，该方法通常用于分类模型从最终输出数据中提取置信度最大的类别序号。同理，有torch.argmin()

1.17. torch.tensor()

将list转为张量

a = [1,2,3,4]
b = torch.tensor(a)

1.18. torch.log()

用于对整体张量取对数，以e为底的对数

t = torch.tensor([1,2,3])
b = torch.log(t)

1.19. torch.topk(tensor,k,dim,largest=True)

该方法主要用于提取前k个最值

tensor：输入张量

k：取前k个最值

dim：指定在哪一维度上取最值，默认为最后一维

largest：默认为True，即取最大值，False为取最小值

该方法通常用于TopK Loss。

a=torch.tensor([1,2,3,4,5])
values,indices=torch.topk(a,2)
# print(torch.topk(a,2))
# 最终会返回一个二元组(values,indices)分别对应值和索引

1.20. torch.abs()

对张量的每个元素求绝对值

t = torch.tensor([-1,1,-2,2,-3,3])
t = torch.abs(t)

2. 神经网络基础概念

人工神经网络（Artificial Neural Networks，简写为ANNs）也简称为神经网络（NNs）或称作连接模型（Connection Model），它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。

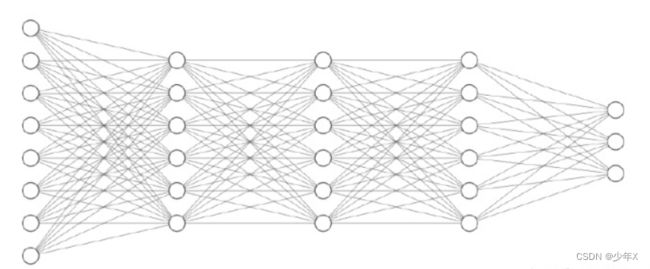
最基础的神经网络模型就是多层全连接，每层的节点之间有“线”相连（y=wx+b），y表示后一层节点，x表示前一层节点，w为权重，b为偏置。如下图：

通常来说神经网络离不开大量的数据，因为其学习的关键步骤就是通过已知样本的输入，进行预测结果的输出，并将预测结果与标签值（即真实值）进行比对，并通过损失函数求得相应的损失值，进而通过损失值进行反向传播，逐层进行梯度更新，并不断循环此过程使得整体模型损失逐渐变小的一个过程。相关过程将在后续介绍。

普通神经网络具体流程：输入 → 模型 → 预测 → 损失函数 → 损失值 → 优化器梯度更新 → 输入 → 模型 → …

3. 反向传播

反向传播即众人所熟知的BP算法，是以梯度下降为基础，通过最终的损失值，通过偏导求得最后一层各节点的下降梯度，并由此向前推出前一层节点的梯度，以此类推，最终实现整个网络每一个节点的梯度求解，并据此进行相关的权重更新以达到向最优解移动的目的。

反向传播的相关实现方法已经进行封装，即使对此过程并不了解也不影响模型的编写和后续的训练，但该理论知识的学习有助于后续对梯度爆炸和梯度消失问题的了解和学习。并且能够更好地理解优化器如SGD的momentum以及学习率lr的概念及作用。

相关的公式推导下面两篇博客已经介绍得很详细了，没必要再进行复述。（两篇博客内容大致相同，可自行选择）

“反向传播算法”过程及公式推导（超直观好懂的Backpropagation）_aift的博客-CSDN博客

一文弄懂神经网络中的反向传播法_神经网络反向传播_爱趣无穷的博客-CSDN博客

视频讲解：【官方双语】深度学习之反向传播算法 上/下 Part 3 ver 0.9 beta_哔哩哔哩_bilibili

相关神经网络可视化学习网站：（可能需要挂梯子）

NNSVG (alexlenail.me)

cbovar.github.io

Jack Cui |Netscope (cuijiahua.com)

CNN Explainer(poloclub.github.io)

ANeural Network Playground (tensorflow.org)

TensorSpacePlayground - LeNet

4. 全连接

如下图所示即为全连接，全连接是指当前层所有节点均与下一层所有节点进行直接相连，每一个节点之间都会有运算。每一个两个节点之间的运算公式为y=wx+b，其中y为后一层节点，x为当前层节点，w为权重，b为偏置。全连接层训练的过程就是不断调整w和b的过程，其中w和b可以手动设置，也可以套用相关的生成算法去进行生成，默认情况下是系统自动生成的。通常来说，一个好的参数初始化模型能够达到更好的效果（但大多数情况下并不需要对模型参数进行手动初始化）。其中偏置可以干掉，但没有特殊需求情况下不建议这么做。

卷积层初始化代码如下：

import torch.nn as nn
LinearName = nn.Linear(in_features,out_features,bias=True)

其中，in_features和out_features为必选参数，分别表示输入和输出特征维度，因此全连接的参数量是in_features*out_features+out_features（前面的乘积是权重，+后面的偏置数量），全连接层的参数不能动态调整（在模型初始化阶段就已经限制好了），因此如果图像识别的网络模型只有全连接结构的话，需要对输入图像进行处理，使之成为预定义大小，如果单纯用全连接限制较多。

5. 卷积

普通的全连接通常用于拟合位置无关或只有在位置上只有一维相关性的数据的神经网络，因此难以学习到二维的特征（理论上来说也并不是学习不到，因为全连接的特性，对于高维特征的提取效果要比卷积好，但对于达到相同效果模型来说，全连接所需要的参数量比卷积核所需要的大得多，很多本身无关的数据之间也有着连接。因此相对来说用全连接代替卷积核去识别图像等，训练时间更长，模型占用空间更大）。视觉学习通常用卷积核来提取图像的特征。具体代码如下：

Conv = nn.Conv2d(in_channels,out_channels,kernel_size,stride,padding,dilation)

通常来说使用Conv2d，即二维卷积核

in_channels：输入通道数，类似全连接的特征维度，这里对应图像的通道数，如RGB的图像是三通道，即channel=3；本参数决定了卷积核深度，必填

out_channels：输出通道数，类比Linear的out_features；本参数决定了卷积核个数，必填

kernel_size：卷积核大小，通常用一个数n来表示一个n*n的二维卷积核（通常来说卷积核是正方形的，并且习惯上用奇数），必填

stride：步长，表示每次卷积核移动的像素数，默认为1

padding：表示填充像素数，会在上下左右每个边填充一列（行）数据（值默认为0），该值默认为0，如果想要在卷积的同时保持图像大小不变可以使该值=kernel_size/2（向下取整，且前提是stride为1，其余情况了解卷积核后可以自行计算）

dilation：默认为0，当该值不为0时为膨胀卷积（也称空洞卷积），并不必须掌握，有兴趣或需求可以了解

5.1 卷积神经网络

卷积神经网络（Convolutional Neural Networks, CNN）是一类包含卷积计算且具有深度结构的前馈神经网络（Feedforward Neural Networks），是深度学习（deep learning）的代表算法之一。卷积神经网络具有表征学习（representation learning）能力，能够按其阶层结构对输入信息进行平移不变分类（shift-invariant classification），因此也被称为“平移不变人工神经网络（Shift-Invariant Artificial Neural Networks, SIANN）

定义：采用监督方式训练的一种面向两维形状不变性识别的特定多层感知机

5.2 卷积核

5.2.1 概念

从计算过程上来理解，卷积核就是对图像像素值的一个区域（kernel_size*kernel_size）大小内的所有值进行加权求和，最终以一个值来代替当前区域的特征值。具体图示如下：

如果单从数据上来看可能不能理解卷积核对于特征提取的作用，下面三张图演示了不同卷积核对原图进行卷积后获得的不同特征图。以下是通过特定的卷积核对图像进行卷积以呈现不同的效果。在实际神经网络训练中，是对卷积核进行随机初始化（同Linear一样也可以手动赋值），并在训练过程中不断调整卷积核的参数以实现不同卷积核对不同特征的提取。

5.2.2 参数计算

对于二维卷积核Conv2d来说，卷积核的输入通道为n，输出通道为m，卷积核大小为k，则其参数量为n*m*kk，通常来说，卷积核个数被认为是输出通道数，即m个卷积核，而卷积核深度（通道）是n（类比一张二维图片，m张二维图片，各有n个通道），每个通道的卷积核都是k*k大小的，因此总的参数量即n*m*kk。具体理解如下图所示：

5.2.3 一维卷积核&三维卷积核

略

5.3 反卷积

如果说卷积是将一张图像抽象成高维特征，那么反卷积就是卷积的逆过程：将高维特征还原为一张图像。但反卷积并不能将卷积后的特征完全复原，只能恢复部分特征。其主要流程是：转置卷积核 → 扩充抽象后的图像 → 卷积 → 原图大小的图像。

Pytorch中声明代码：nn.ConvTranspose2d()

6. 池化

池化过程通常在卷积之后，对卷积后的图像进行下采样，在适度保留特征的前提下减少图像的体积，以加快运算，提高训练、预测速度。

其中常采用的一种方法是最大池化（Max Pooling），代码如下：

pool = nn.MaxPool2d(kernel_size)

其中，池化也可以视为一个卷积核，对图像进行卷积操作。池化的范围为kernel_size，并且与卷积核相似，池化也有stride、padding、dilation，并且作用相同，但默认池化的stride=kernel_size，即每次进行池化原图像在w和h上都会缩小kernel_size倍。

平均池化，用法和初始化与最大池化相同，其将会提取整个区域的平均值作为池化的最终值

pool = nn.AvgPool2d()

思路：全局平均池化

全局平均池化并没有在Pytorch中以单独方法实现，但可以使用torch.mean()来进行。此方法能够将任意尺寸的图像作为输入，并且最终输出相同尺寸的值，该值可用作固定的全连接网络的输入或者直接作为输出使用，能够很好地适配内部网络连接尺寸，从而解决解决CNN和FCN（如果含有Linear的话）必须固定尺寸的问题。

7. 构建神经网络

神经网络是一层层模型堆积而成，一个简单的神经网络模型只需要一个含有两个方法（__init__和forward）的类，其中__init__()用于模型初始化，并对一些参数进行配置；forward(input)用于模型的前向传播。

import torch.nn as nn
    
class SelfModel(nn.Module):
	def __init__(self):
		super(SelfModel, self).__init__()
		#在此处声明各层网络结构
    
	def forward(self, input):
		#在此处进行各层网络调用
    
		#return output 

#模型实例化及调用方法：

net = SelfModel()
pre = net(data)        #data为输入数据，pre为输出数据，该行代码等价于net.forward(data)，
# loss...

#如一个多分类CNN网络：

import torch.nn as nn
    
class SelfModel(nn.Module):
	def __init__(self):
		super(SelfModel, self).__init__()
		self.Conv1 = nn.Conv2d(3, 8, 3, 1, 0)
		self.Conv2 = nn.Conv2d(8, 16, 3, 1, 0)
		self.Conv3 = nn.Conv2d(16, 32, 3, 1, 0)
    
		self.flatten = nn.Flatten()
    
		self.Linear1 = nn.Linear(100, 1000)        # 此处默认认为卷积后的数据元素数量为100
		self.Linear2 = nn.Linear(1000, 10)
    
		self.ReLU = nn.ReLU(inplace=True)
		self.Maxpool = nn.MaxPool2d(2)
		self.Softmax = nn.Softmax()
    
	def forward(self, input):
		x = self.Maxpool(self.ReLU(self.Conv1(input)))
		x = self.Maxpool(self.ReLU(self.Conv2(x)))
		x = self.ReLU(self.Conv3(x))
		x = self.flatten(x)
		x = self.ReLU(self.Linear1(x))
		x = self.Softmax(self.Linear2(x))
		return x

8. 激活函数

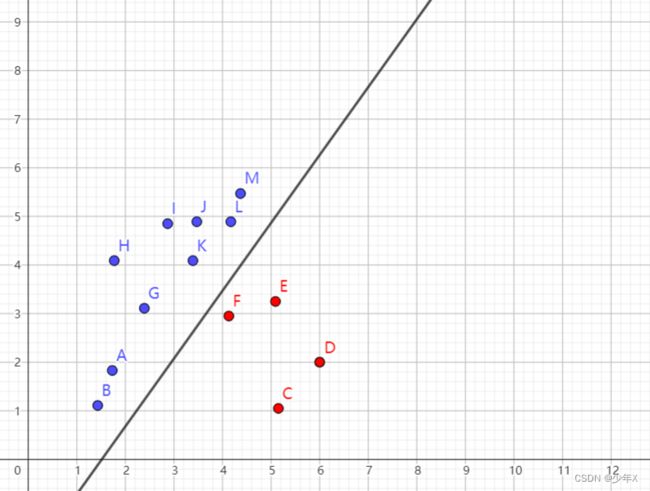
通过上面的学习不难发现，在神经网络中，无论是卷积池化还是全连接，都是大量的线性计算堆积的。因此就会造成一个问题：只能解决线性问题。如对下面图1坐标系中的一些离散点按照颜色切分，使用线性网络可以很好地划分；但如果要求对下面图2的坐标系中的离散点进行划分，则使用线性网络难以实现。即使是多层线性网络堆积的效果还是一样的，依旧是一个线性关系，如节点1 $y_1=w_1{x}_1+b_1$ 和节点2 $y_2=w_2{x}_2+b_2$ 进行叠加计算，最终的公式为$y_2=w_2(w_1{x}_1+b_1)+b_2$ 即 $y_2=w_2{w}_1{x}_1+b_1+b_2$ ，输出$y_2$和输入$x_1$依旧是线性关系。由此引出激活函数，通过非线性运算（激活函数是非线性的，线性与非线性进行运算最终依旧是非线性的）来使得神经网络的计算由原来的线性变为非线性，从而更好地拟合形势复杂多变的数据。

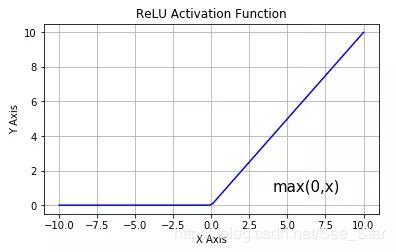
7.1. ReLU

ReLU是神经网络中一种最为基础的激活函数，同时也是最常见的，但随着对模型精度要求的不断提高，传统的ReLU并不能满足所有的网络，因此并不可一味地使用ReLU作为激活函数。

relu = nn.ReLU(inplace=True)

inplace参数是指原地操作即将relu后的张量数据赋值给原来的张量，能够节省内存（显存），默认为False即不采用该操作。但并不是所有的激活函数都能进行该操作。其他激活函数是否支持可以尝试声明该参数或查阅一下资料。

ReLU是简单的分段函数，公式如下

$$ReLU(x)=max(0,x)=\{\begin{array}{ll}0& x⩽0\\ x& x>0\end{array}$$

相对于其他激活函数来说，ReLU的简单能够使得梯度下降和反向传播更具有效率，并且能够有效地避免梯度爆炸和梯度消失问题，并且计算成本较低。但同时也带来一个问题，即lr较大时会造成神经元死亡的问题，具体推导见链接 relu激活函数的缺点 - 知乎 (zhihu.com)

7.2. LeakyReLU

LeakyReLU的提出主要是为了解决ReLU在训练过程中出现神经元“die”的问题，主要方法为在负轴上采用一个很小的常数以保留负坐标的值。如下图：

leakyRelu = nn.LeakyReLU(inplace=True)

公式如下

$$LeakyReLU(x)=max(0.1x,x)=\{\begin{array}{ll}0.1x& x⩽0\\ x& x>0\end{array}$$

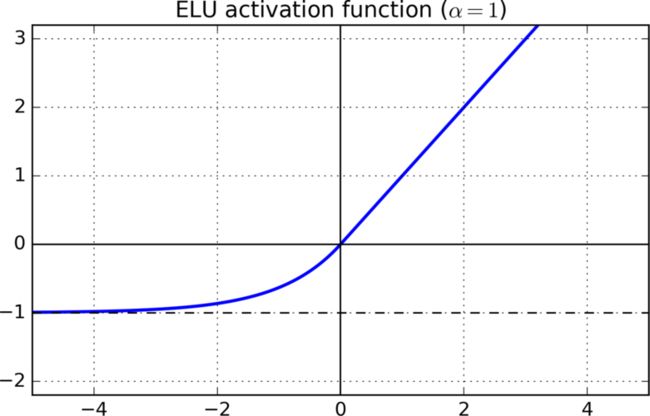
7.3. ELU

与 Leaky-ReLU 和 PReLU 类似，与 ReLU 不同的是，ELU 没有神经元死亡的问题(ReLU Dying 问题是指当出现异常输入时，在反向传播中会产生大的梯度，这种大的梯度会导致神经元死亡和梯度消失)。 它已被证明优于 ReLU 及其变体，如 Leaky-ReLU(LReLU) 和 Parameterized-ReLU(PReLU)。 与 ReLU 及其变体相比，使用 ELU 可在神经网络中缩短训练时间并提高准确度。

elu = nn.ELU(inplace=True)

$$ELU(x)=\{\begin{array}{ll}\alpha (e^x-1)& x⩽0\\ x& x>0\end{array}$$

α超参数一般取1

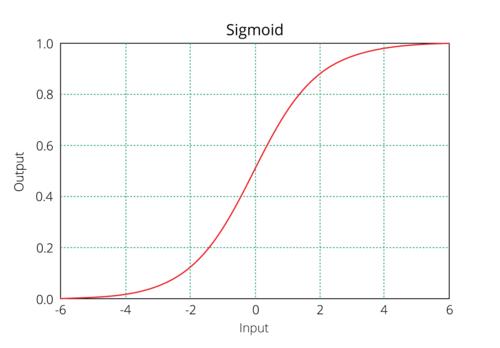
7.4. Sigmoid

tanh和Sigmoid又被称为饱和激活函数，而ReLU及其变种被称为非饱和激活函数。通常来说，ReLU系激活函数用于隐藏层，而tanh、Sigmoid、Softmax通常用于输出层。并且ReLU系的值域为∞，而Sigmoid、Softmax的值域为(0,1)，tanh的值域为(-1,1)

Sigmoid函数也被称为Logistic，其通常用作回归。并且其值域为(0,1)，因此符合归一化的范围，通常可直接用作对输出数据进行归一化，使其映射到(0,1)范围中。在YOLOV2中用于对Anchor的x、y、w、h以及confidence的最终输出的结果进行激活处理。相对来说，Sigmoid有平滑且易于求导的特点。但也会引起几个问题：

（1）计算量很大：因其是一个分数且分母的项中有幂运算

（2）易容易出现梯度消失的问题

（3）0均值问题：通常情况下，Sigmoid不会出现在隐藏层中，如果在最后输出层使用Sigmoid激活函数则不会出现该问题

sig = nn.Sigmoid()

$$Sigmoid(x)=\frac{1}{1+e^{-x}}$$

7.5. tanh

tanh双曲正切函数，与Sigmoid相似，属于饱和激活函数。但其值域为(-1,1)，能够解决Sigmoid的0均值问题，并且在梯度消失的问题上相对于Sigmoid有所缓和，但依旧涉及幂运算，相对来说效率较低。

tanh = nn.Tanh()

$$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}\text{\hspace{1em}(1)}$$$$tanh(x)=\frac{2}{1+e^{-2x}}-1\text{\hspace{1em}(2)}$$

7.6. Softmax

与tanh和Sigmoid对单个数据进行激活不同，Softmax是将一组数据（一维张量）进行激活处理，即将一组数进行幂运算，之后各自除上这一组幂运算后的数值的总和，即对数据进行归一化处理，每一个数据都是分布在[0,1]区间内的一个值，并且这一组数求和恒为1。因此Softmax绝大多数情况下用于分类并且是多分类的情况，在每次预测时有且只有一个类别可能会出现大于0.5的情况。通常情况下Softmax与NLLLoss损失函数同时出现，但在NLLLoss进行损失计算之前需要先对Softmax输出取对数，否则会出现负值情况。

softmax = torch.Softmax()

存在问题：

如下公式，如果x过大，当超过一定值时，会趋向于无穷大，此时值会变为inf，即Softmax的上溢问题

同样，当x足够小时（-x），会无限趋近于0，因为精度有限，较小的值将由0表示，如果每一项都是过小的值（此处均指负数）则会出现Softmax输出各项求和为0的情况，称为Softmax的下溢。

$$Softmax(z_i)=\frac{e^{z_i}}{{\sum }_{c=1}^C{e}^{z_c}}$$

7.7. Softmax2d

Softmax是对一维数据进行激活处理，同理Softmax2d是对二维数据进行激活处理，但这里的二维并非是指将整个二维的数据算作一个“组”。如输入一张图像[N,C,H,W],其中，Softmax2d是对C这一维度进行求和与运算，即H*W的平面上每一个深度为C的列可以看做一个一维张量，对此张量进行Softmax激活运算。

7.8. LogSoftmax

即对Softmax取对数，当然也可以手动调用torch.log()对Softmax处理后的数据取对数，二者意义相同。但LogSoftmax的求导比Softmax更容易，并且解决了Softmax存在的上下溢问题。相对来说LogSoftmax比Softmax取对数具有更好地性能并且能够解决上下溢问题。但Pytorch库中只有LogSoftmax没有LogSoftmax2d，因此想要进行二维运算依旧需要使用Softmax2d。

7.9. 其他

更多的损失函数访问链接：激活函数汇总 - 知乎 (zhihu.com)

9. 损失函数

通常来说，如果要训练一个好的神经网络模型，离不开数据、模型、损失函数，损失函数是一个模型当下预测表现的一种评估方法。由于神经网络的输入、输出、模型结构以及数据等都不是一成不变的，因此损失函数也并不是唯一或者是固定的几种。通常来说需要根据具体需求以及输入输出等自行编写损失函数。损失函数主要用于计算损失值，并进行反向传播计算模型各节点的参数下降梯度，因此一个好的损失函数是必需的。通常来说损失函数的编写需要考虑数据的形式、数量、样本均衡程度、输出数据的shape等多方面因素，并且在训练过程中根据训练的效果、测试结果进行调整。

9.1. NLLLoss

NLLLoss，负对数似然损失函数。用于处理多分类问题，通常与LogSoftmax(x)或log(Softmax(x))共同使用。NLLLoss其实并没有什么复杂的公式，其实就是将label中对应位置的值作为输出值的索引，并获取该位置值的相反数，作为本组数据的最终损失，并对每组数据执行上述操作，之后对整体取平均值即为此次迭代的损失值，示例如下：

如输入一个二维数据（3组值，假设每组有五个类别）

       t=[[.1,.2,.3,.3,.1],                                右侧为预测的输入值，左侧为label                [1,2,4]                第一组的标签是1即t[0,1]是损失，为 - 0.2

         [.1,.1,.6,.1,.1],                                                                                                                                      同理，第二组为t[0,2]                         - 0.6

         [.05,.1,.15,.2,.5]]                                                                                                                                  t[0,4]                                                    - 0.5

    因此上述的NLLLoss损失为-0.4333333，但通常来说损失是一个整数，因此预测的值应该取对数使其变为负对数

声明代码：

Loss = nn.NLLLoss()
# Loss = nn.NLLLoss().cuda()如果要用GPU进行训练，Model和Loss以及输出的tensor均要使用.cuda()
# Loss = nn.NLLLoss().cpu()可以用.cpu()和.cuda()来进行切换，默认是在CPU下进行，所以初次声明无需显式调用.cpu()
# 所有的损失函数都遵循上述设备切换方式

上述示例实现代码：

t = torch.tensor([[.1, .2, .3, .3, .1],
				  [.1, .1, .6, .1, .1],
                  [.05, .1, .15, .2, .5]])
label = torch.tensor([1, 2, 4])
Loss = nn.NLLLoss()
loss = Loss(t, label)
print(loss.item())
# 输出结果为 -0.4333333671092987

同样，NLLLoss也有对应的二维版本NLLLoss2d，对比Softmax

9.2. MSELoss（L2Loss）

MSELoss，均方损失函数，又称为L2Loss，在Pytorch官方中称为MSELoss。声明代码如下：

mseLoss = nn.MSELoss()

顾名思义，MSELoss就是预测值与真实值差的平方，并对此求平均数。MSELoss通常用于回归问题。

$$MSELoss=\frac{1}{M}\sum _{i=1}^n{(y_i-x_i)}^2$$

代码样例：

mseLoss = nn.MSELoss()
pre = torch.tensor([[1, 2, 3], [4, 5, 6]]).float()
label = torch.tensor([[8, 9, 10], [11, 12, 13]])
loss = mseLoss(pre, label)
print(loss.item())

9.3. L1Loss（MAELoss）

虽然MAELoss又叫L1Loss，但此处题目采用L1Loss的原因是在Pytorch中并没有以MAELoss进行命名，而是使用L1Loss。MAELoss，平均绝对误差。

maeLoss = nn.L1Loss()

$$MAELoss=\frac{1}{M}\sum _{i=1}^m|y_i-x_i|$$

代码样例：

l1Loss = nn.L1Loss()
pre = torch.tensor([[1, 2, 3], [4, 5, 6]]).float()
label = torch.tensor([[8, 9, 10], [11, 12, 13]])
loss = l1Loss(pre, label)
print(loss.item())

如何在回归预测中选择MAE还是MSE

从误差的角度来说：MSE可以用来评价数据变化的成都，MAE则能更好的反应预测值误差的实际情况

从离群点的角度选择：如果离群点仅仅只是在数据提取的过程中损坏或者清晰中的错误采样，则无需给予过多关注，应当选择MAE；但如果离群点是实际的数据或者重要的数据，是需要被检测到的异常值，应当选择MSE

从收敛速度的角度来说：MSE>MAE

从求解梯度的复杂度来说：MSE要优于MAE，且梯度也是动态变化的，MSE能较快准确达到收敛

从模型的角度选择：对于大多数CNN网络，我们一般是使用MSE而不是MAE，因为训练CNN网络很看重训练速度，对于边框预测回归问题（如YOLO等），通常也可以选择平方损失函数，但平方损失函数缺点是当存在离群点的时候，这些点会占loss的主要组成部分。对于目标检测Fast RCNN采用稍微缓和一点的绝对损失函数（smooth L1），它是随着误差线性增长而不是平方增长。

9.4. smooth L1

如果看L1 Loss和L2 Loss的导数不难发现，L1 Loss的导数中心点是折点，不能进行求导，且L1 Loss的导数为常数；而L2 Loss的导数虽然比较平滑且非常数，但出现离群点时梯度会非常大，容易出现梯度爆炸的情况。而smooth L1则是通过进行分段的方式融合了L1 Loss和L2 Loss的优点并且避开了二者的缺点，使得其在损失较小时避开导数为常数的现象，并且当误差很大时导数为常数。

smoothLoss = nn.SmoothL1Loss()

$$smoothL1=\{\begin{array}{ll}0.5(y_i-x_i{)}^2& -1<x<1\\ |x|-0.5& otherwise\end{array}$$

代码样例：

smoothL1Loss = nn.SmoothL1Loss()
pre = torch.tensor([[1, 2, 3], [4, 5, 6]]).float()
label = torch.tensor([[8, 9, 10], [11, 12, 13]])
loss = smoothL1Loss(pre, label)
print(loss.item())

9.5. CrossEntropyLoss

CrossEntropyLoss，交叉熵损失函数。为理解“熵”这个概念，首先需要了解一下香农对信息论中信息熵用数学语言进行的阐释：

$$H(X)=-\sum _{x}p(x)lo{g}_{2}p(x)$$

信息量：表示数据资料消除人们认识上的不确定性的大小，该大小就是此数据资料的信息量。信息量的量化方法即对该事件发生的概率取负对数。由此可知，当一件事发生的可能性越高，信息量越接近于0，当其概率无限接近于0时，信息量无穷大。

信息熵（information entropy）是信息论的基本概念，用于表示信息量的期望。即信息源各种可能事件发生的不确定性进行加权平均并将求得概率与信息量相乘后求和。

信息熵示图

交叉熵概率取值分布热力图

注：底侧的p为真实概率；-log(p)中的p为预测概率

交叉熵（Cross Entropy）是Shannon信息论中一个重要概念，主要用于度量两个概率分布间的差异性信息。语言模型的性能通常用交叉熵和复杂度（perplexity）来衡量。交叉熵的意义是用该模型对文本识别的难度，或者从压缩的角度来看，每个词平均要用几个位来编码。复杂度的意义是用该模型表示这一文本平均的分支数，其倒数可视为每个词的平均概率。

更为直观地解释：交叉熵是信息熵的另一种“形式”，二者公式相同，只不过对于概率的描述有所不同，交叉熵更偏重于自己所认为的概率与实际发生的样本之间的差距，即令自己的预测与真实数据之间的差距让自己的吃惊程度。CrossEntropyLoss公式如下，其中对数部分即自己认为的概率，$y_i$为真实的样本分布概率，二者的乘积即当前事件的期望。由上图（交叉熵概率取值分布图）不难发现，当概率与信息量相近时（此处的概率是指预测概率，真实概率与信息量是负对数关系，因此此处的相近指的是预测概率与信息量更接负近对数关系，也即预测概率与真实概率更接近。$((p\to 1)and(-log(p)\to 0))or((p\to 0)and(-log(p)\to +\infty ))$），期望（误差）相对较小，但如果概率与信息量相差较大时（同上，指的是p→1&-log§→+∞），期望会变趋向于+∞（图中由于粒度限制，最小值取0.01，因此图中最大值为6.6438（$lo{g}_2(p)$））。这也符合损失函数的意义：客观衡量真实值与预测值之间的差值。因此可以用交叉熵来作为分类的损失函数，用来评判预测概率的误差。

但通过上图也引出一个问题，当真实值$p\to 0$时，如果$-log(p)\to +0$即预测概率$p\to 1$并不会产生很大的误差，相反，二者的期望和预测概率与真实概率接近的期望走势基本相同：$E\to 0$这也就解释了为何在Pytorch中如果使用小数（即使是1.0）会报错，当真实概率小于1时的误差计算是不准确的，因此$p\ne 1$并没有实际意义，所以CrossEntropyLoss并不能参与真实值为小数的运算。

# 上图热力图的绘制代码
import matplotlib.pyplot as plt
import numpy as np
k = 100  # 粒度
ax = plt.subplot(projection='3d')
x = np.array([i / k for i in range(1, k + 1)])
y = -np.log(x)
x, y = np.meshgrid(x, y)
z = x * y
z = np.reshape(z, [k, k])
ax.plot_surface(x, y, z, cmap='rainbow')
ax.set_xlabel('p')
ax.set_ylabel('-log(p)')
ax.set_zlabel('H')
plt.show()

$$\begin{gathered} CrossEntropyLoss=\sum _{i=1}^n{y}_{i}lo{g}_e{x}_i \\ 此处测x_i是已被LogSoftmax映射后的概率值 \end{gathered}$$

CrossEntropyLoss初始化：

entropyLoss = nn.CrossEntropyLoss()

CrossEntropyLoss的输入与其他损失函数一样，是预测值pre和标签label，与NLLLoss相同，每一个值代表一组数据的真实类别索引，如果想要更好地理解其运算过程，可以将其转化one-hot，如下面样例代码中的[1,2]可以转为[[0,1,0,0],[0,0,1,0]]，据此与每个数据进行交叉熵运算即可。

entropyLoss = nn.CrossEntropyLoss()
pre = torch.tensor([[.25, .25, .25, .25],[.3,.4,.5,.6]])
label = torch.tensor([1,2])
loss = entropyLoss(pre, label)
print(loss.item())      

注：CrossEntropyLoss = Softmax + log + NLLLoss 或 LogSoftmax + NLLLoss，因此使用CrossEntropyLoss无需再使用Softmax对输出进行激活。虽然使用CrossEntropyLoss可以简化步骤（并且理论上来说集成的步骤比分解步骤更容易进行整体上的优化，但在此不做讨论，后续可能会展开对一些计算代码的分析。因此至于性能上是否会有所提升持保留态度），但CrossEntropyLoss带来的问题是最后的输出层的值并没有进行一个[0,1]映射，有可能不同的输入数据最后的输出不在一个数量级上（虽然依旧可以用argmax来求最大索引，但如果需要对概率进行后续的计算工作，可能依旧要使用Softmax）。但同样的，如果需要计算交叉熵的网络层在内部隐藏层中，如果在内部嵌入Softmax，会导致一些高纬度信息丢失（如数量级等），因此更建议使用CrossEntropyLoss。

9.6. BCELoss

BCELoss，全称Binary Cross Entropy，即二元交叉熵，常被用来当作二分类的损失函数，与CrossEntropyLoss的多分类不同的是，二分类是判断一个样本是正样本还是负样本，也就是True or False，因此可以用一个区间为[0,1]的值来决定这个二分类样本的预测，即有多大的概率p是T，则1-p的概率为F。所以二分类并不需要像多分类一样每一个类别都需要进行一个预测并最终生成一个向量，因而也就不需要Softmax激活函数进行映射，但依旧需要将其收敛到[0,1]区间内，因此可以用Sigmoid来进行激活。所以BCELoss与CrossEntropyLoss很明显的一个区别即没有内置Softmax，公式如下：

$$BCELoss=\frac{1}{N}\sum _i-[y_i\cdot log(p_i)+(1-y_i)\cdot log(1-p_i)]$$

BCELoss初始化：

bceLoss = nn.BCELoss()

对于BCELoss不含Softmax的验证：

# CrossEntropyLoss
entropyLoss = nn.CrossEntropyLoss()
logp = torch.tensor([[.25, .4]])
p = torch.tensor([1])
loss = entropyLoss(logp, p)
print(loss.item())        #0.62095707654953

# BCELoss
bceLoss = nn.BCELoss()
logp = torch.tensor([[.25, .4]])
softmax = nn.Softmax()
p = torch.tensor([[0.,1.]])
loss = bceLoss(softmax(logp), p)
print(loss.item())        #0.62095707654953

BCELoss的label.shape要与pre.shape相同，并且pre不可超出区间[0,1]，但label并没有规定区间，并且并非必须是0/1整数，可以是任意小数甚至是负数，但通常情况下非0/1的样本值是无意义的。

9.7. Focal Loss

Focal Loss并不是一种具体的损失函数，而是表示一类损失函数，也表示一种处理样本不均衡的思想，因此在Pytorch中并无相对应的实现方法，需要自己根据模型和相关目的自主编写对应的损失函数。

首先来介绍一下什么是样本不均衡。因为大部分的神经网络是属于监督学习或半监督学习，因此就必然离不开大量的数据支撑。如二分类：当你要写一个模型去判断一张图片是否有人物的时候，必然会搜集大量的图片来当作训练数据。如果使用爬虫进行随机图片爬取，必然会出现的结果是含有人物的图片数量远少于不含有人物的图片，也就是说正样本数量远少于负样本。这样做会产生一个很严重的问题，因为神经网络是通过损失函数最终求得的损失值进行梯度更新的，换句话说就是基于大量数据训练而成的统计模型。因此每一次梯度更新必然是向着整体损失偏小的方向前进，如果负样本数量远多于正样本，如训练数据中正负样本的比例是1：99，神经网络大可以将所有的输入样本判定为负样本，而训练集的精度可以轻易达到99%。但这样的网络是没有意义的，这也就是样本不均衡问题。

如果是上述样本不均衡问题，可以通过爬虫有选择的对图片进行爬取以平衡人物图片与非人物图片的比例从而实现均衡。但试想如果是多分类，如Pascal Voc的样本（以下两张图分别是Pascal Voc 2007和Pascal Voc 2012的二十类图片比例），进行人工标注来扩充数据集需要耗费大量时间，并且含有其他类别的图片往往都含有person这个类别，因此对于有些数据集来说增加样本的方法时间、人工成本会很高。即使能够使上述数据集做到样本均衡，那让我们换个角度去想，如果我需要做一个模型去预测在某天是否会发生火山喷发呢？对于极其有限并且不可再生成的正样本，上述方法不再可行，只能通过其他的方法来实现样本均衡。

其他解决的样本不均衡方法之后再展开，这里介绍一种实现起来较为简单的方法：通过权重来实现正负样本的损失均衡。

通过权重来解决样本不均衡的方法其实很好理解。通常我们不会用所有样本去直接训练一个网络，因为一个现实因素的限制——显存（内存），虽然全部样本进行训练每次都是当下的全局最优，但多次的局部最优也能起到相似的作用。因此通常将数据分为一个batch（批），一个batch的大小称为batchsize，比如训练图片分类，通常使用16-256之间的一个数（太大或太小都不好，视具体情况而定，后续会再进行讨论），即一次输入一个batchsize张图片求整体的损失。一般来说，并不会单纯地将所有的图片分为一个个batch，因为这样会让网络学习到输入数据的顺序，从而降低模型的泛化性。因此会进行随机抽样，每次从中抽取batchsize个样本作为一个batch，此时batch中的正负样本比例近似为整体样本中的正负样本比例，假设为m：n。如果对其求损失的话，假设每个样本的损失都约为0.5，则正样本的整体损失为0.5m，负样本整体损失为0.5n。如果m：n为1：10，则整体损失为55，正负样本损失比为5：50。模型自然会向着负样本的方向下降。但此时如果将正负样本损失分别乘上对方的样本比例，即0.5m*10与0.5n*1，则正负样本损失比为1：1，这也就实现了均衡的目的。

Focal Loss就是采用了这种思想，但与此不同的是其并不是根据样本来决定权重，而是基于概率，即当前样本可分的难易程度。基础公式依旧采用交叉熵，但在前面添加一个根据权重，公式如下：

$$FocalLoss(p_t)=-(1-p_t{)}^{\gamma }log(p_t)$$

其中，γ是一个超参数，试验值如下：

超参数γ的取值依据具体正负样本的区分难易程度和样本不均衡程度决定，并无唯一的参考值，γ越大，难分样本的损失贡献越大，当γ为0时，Focal Loss退化为CrossEntropyLoss。

通过公式可以看出，当概率与实际差值越大时，权重越大，相应的求得的损失也越大。与根据样本数直接修改正负样本不同的是，该方法是基于预测结果来调整权重，即从样本难易程度，而非单单只是取数量的不均衡程度。因此从这个角度来看，一般是要优于前面提到的样本数作为权重的方法的。

9.8. TopK Loss

TopK Loss旨在关注训练数据中的难分样本。与Focal Loss不同的是，TopK Loss并不通过权重来改变各样本的损失值，而是求得每个输入样本的损失，并且取排行前K个的损失作为当前迭代的损失值，直接用难分样本作为损失，去掉大量容易样本的影响，在一定程度上能够促进模型对难分样本的学习。但同样的，在注重难分样本的同时会降低模型对易分样本的关注，大量易分样本的精度会有所下降，损失上升，导致平均损失上升。

9.9. 自定义 Loss

一般来说一些复杂的、同时具有多种功能的模型需要多个损失函数进行组合，甚至需要自己编写损失函数来对网络进行评估和更新。

如一个简单的MAELoss的自定义方式实现：

import torch
import torch.nn as nn

class Loss(nn.Module):
    def __init__(self):
        super(Loss, self).__init__()

    def forward(self, pre, label):
        return torch.mean(torch.abs(pre - label))

自定义损失函数的编写方式和神经网络模型编写方式一样，只不过并没有网络结构，因此__init__()中并不需要进行额外的定义，不过如果想要在初始化损失函数的时候定义一些权重参数等也是可以的。

9.10. 损失函数的使用

借9.9定义的损失函数来举例：

loss = Loss()
data,label = ...        #此处省略，数据和标签读取
net = NEt()
pre = net(data)
loss_result = loss(pre,label)
loss_result.backward()        #反向传播，在求得损失后必须调用该方法进行反向传播来计算模型各层各节点的梯度

10. 优化器

10.1. SGD

SGD为随机梯度下降，通常为固定学习率（当然也可以使用相应的方法对SGD的lr进行相应的调整），SGD通常使用三个参数，param、lr、momentum，分别表示模型参数、学习率、动量。具体使用方式如下：

import torch.nn as nn
import torch.optim as optim

class NET(nn.Module):
    def __init__(self):
        super(NET, self).__init__()

    def forward(self):
        pass

net = NET()
optimizer = optim.SGD(net.parameters(), lr=.1, momentum=.99)  #其他的优化器使用方法相同，只需要替换SGD和相应参数即可
  
 # 训练过程
for i in range(1000):
    data,label = Read()  #假设已经读取了数据和标签
    optimizer.zero_grad()   #清空梯度
    pre = net(data)        #预测
    loss = Loss(pre,label) #求损失
    loss.backward()        #反向传播       
    optimizer.step()       #更新模型梯度  

其中，第一个参数是固定格式，第二个参数是学习率，如果看过上面给的关于反向传播链接可以知道：学习率lr决定了梯度更新的大小，即模型优化的步长。当学习率较大时，梯度更新大，容易造成模型的不稳定；但同样的，如果学习率较小，梯度更新小，模型收敛较慢。初期如果lr较大，容易跑飞（nan、inf等），不同模型情况不同；后期如果lr较大会出现模型一直在以一个较大的振幅不断震动也很难有效收敛。如果lr较小，在初期容易收敛较慢。并且lr较小还会引发一个问题：局部最优。理论上来说神经网络就是一个不断求当前模型下局部最优解，但通常来说最终模型会落在谷底（又称峡谷）或鞍点，如果此时在谷底之外还有个更优解，则模型将无法收敛得到一个更好的结果。此时如果增大学习率让模型冲出去也是可以的，但在训练过程中准确预测谷底并适当调整学习率是不现实的，因此加入了第三个参数：动量，让模型能够在谷底获得一个不断累加的动量来跳出局部最优去寻找一个更好的结果。

动量的作用不仅局限于此，如果你对梯度下降有一个更清晰的认识，就会意识到一个问题：当某一个方向的梯度相对较大时，模型会给予这个方向更大的分量，从而使得模型在起伏较大的方向上剧烈的抖动以试图寻找最低点，但是对分量较小的方向下降十分缓慢（可以想象一下一个十分深的具有光滑曲面的峡谷，峡谷底部坡度十分小，而峡谷本身的坡度很大，此时在顶端放一个小球任其自由下落，小球更多的是在峡谷石壁两侧来回剧烈运动，但在沿着峡谷谷底方向上缓慢移动着）。此种情况会导致模型收敛速度很慢，因此加入动量会在很大程度上缓解这个问题。具体的理论依据如链接：SGD动量法和Nesterov加速梯度下降法 - 简书 (jianshu.com)

10.2. Adam&Adadelta

这俩个并没有深入太多的研究，参数其实只需要SGD的第一个即模型参数就够了，只需要知道：相对于SGD，Adadelta和Adam都不需要指定学习率，它们本身会自动更新学习率，并且相对于SGD来说能够更快地收敛到一个较好的点。但据说，SGD在科研论文中的使用比例依旧要大于Adadelta和Adam，更深入的东西并没有研究，但就普遍效果来看，SGD最终收敛效果要更好一些（但并不是绝对的）。因此如果想要快速验证模型可行性，或者快速开发可以使用Adam和Adadelta，好处是不需要频繁调整学习率来获得更好的模型（这里要提一句，学习率过大或过小都会影响模型最终效果）。但如果追求更高精度，相对来说还是建议使用SGD。

10.3. Adadelta

11. 其他相关名词

学习率 lr

BN

泛化性

鲁棒性

过拟合

欠拟合

上采样

下采样

样本不均衡

噪声

优化器总结 https://zhuanlan.zhihu.com/p/22252270

机器学习评估指标

前置知识

训练集、测试集、验证集

IOU

MAP

ACC

Recall

f1-score

机器学习常见问题

机器学习常用方法

归一化

正则化

L1

L2

Dropout

标准化

相关库介绍及使用

1. OpenCV

2. matplotlib

plt.cla和clf区别，前者清除plt的plot后者清除所有的如ax的plot

3. pandas

4. torchvision

5. PIL

6. numpy

7. sklearn

8. Keras

视觉学习

图像增强

噪声

椒盐噪声

随机缩放、裁剪

随机翻转

随机亮度、灰度、明度、对比度

图像分类过程示例

目标检测

YOLOV2

Fast-CNN

集成模型

1. Stacking

2. Boosting

3. GBDT

4. Bootstrap

5. Bagging

强化学习

生成对抗网络

迁移学习

自然语言

1. CBOW

2. Skip-gram

3. Word2vec

GNN

听觉学习

监督学习

半监督学习

无监督学习

Kmeans聚类、knn

精度节省内存

爬虫

多标签分类问题的损失函数与长尾问题_多标签分类损失函数_王文浩1997的博客-CSDN博客