【数据结构】线性表-线性表的顺序表示和实现

一、线性表的数据对象SqList

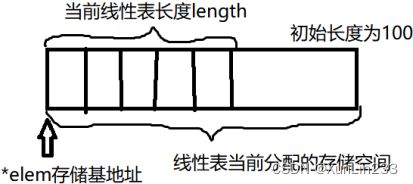
1.初始分配量:LIST_INIT_SIZE

2.分配增量:LISTINCREMENT

3.基地址:elem

4.当前长度:length

5.当前分配的存储容量:listsize

#define LIST_INIT_SIZE 100  //初始分配量
#define LISTINCREMENT 10  //分配增量

typedef int ElemType;

//数据对象
typedef struct {
	ElemType* elem;  //该线性表的基地址
	int length;  //当前线性表的长度
	int listsize;  //当前分配的存储容量
}SqList;

二、线性表初始化InitList_Sq

//初始化线性表
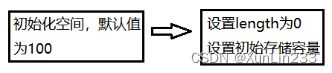
bool InitList_Sq(SqList& L) {
	L.elem = (ElemType*)malloc(LIST_INIT_SIZE * sizeof(ElemType));  //初始化空间
	if (!L.elem) return false;  //判断初始化空间是否成功
	L.length = 0;  //初始长度为0
	L.listsize = LIST_INIT_SIZE;  //线性表分配空间长度
	return true;
}

 

三、插入元素ListInsert_Sq

分析：

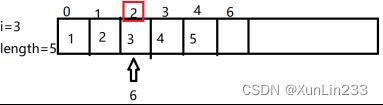
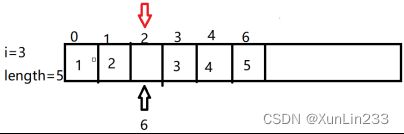
（1）在线性表第三个位置，也就是下标为2的位置插入元素6

（2）现在要让下标为2的位置空出来，但又要保证后面的元素不变，这个时候我们就要让元素统一向后移，在下标为2的地方空一个位置出来。

让指针指向最后一个元素，将指向的值往后移一位。也就是将当前指针指向的值赋值给指针+1的位置。

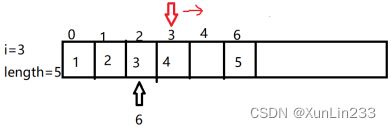
（3）移动完后指针位置-1，继续上一步的操作

 

（4）继续上一步操作

 

（5）一直移动到i-1的位置结束，移动完后下标为2的位置空出来了

 

（6）将6赋值给指针指向的位置，线性表长度+1

总结：

//线性表中插入元素
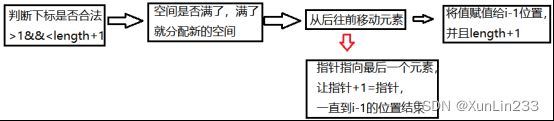
bool ListInsert_Sq(SqList& L, int i, int num) {
	if (i<1 || i>L.length + 1) return false;
	if (L.length > L.listsize) {  //存储空间已满，分配增量
		ElemType* newspace = (ElemType*)realloc(L.elem,(L.listsize + LISTINCREMENT) * sizeof(ElemType));
		if (!newspace) return false;
		L.elem = newspace;  //重新赋值基地址
		L.listsize = L.listsize + LISTINCREMENT;  //改变存储容量
	}
	ElemType* p = &L.elem[i - 1];  //下标为i-1的地址
	for (ElemType* q = &L.elem[L.length - 1]; q >= p; q--)
		*(q+1) = *q;  //从length - 1 到 i - 1 进行移位操作
	*p = num;  //将值赋给下标地址
	L.length++;  //线性表长度+1
	return true;
}

 

四、删除元素ListDelete_Sq

分析：

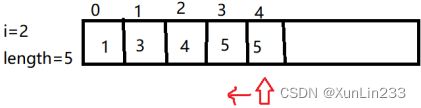
（1）在线性表第二个位置，也就是下标为1的位置删除该元素

 

（2）让指针指向i的位置，也就是删除元素的后一个位置，将该数往前移

 

（3）将指针指向的值赋值给指针-1的位置后，指针向后移动一位，继续元素位移操作

 

（4）继续上一步操作

（5）一直到指针指向为length-1结束

 

（6）移动结束后让length长度-1，不用担心4的位置有元素，线性表长度为4，只会到下标为3的位置

总结：

 

//线性表中删除元素
bool ListDelete_Sq(SqList& L, int i, ElemType& e) {
	if (i<1 || i>L.length + 1) return false;
	ElemType* p = &L.elem[i - 1];  //删除元素的地址
	e = *p;  //将删除元素赋值给e
	p = &L.elem[i];
	for (ElemType* q = &L.elem[L.length - 1]; p <= q; p++)
		*(p - 1) = *p;  //从i到legnth-1开始往前移位操作
	L.length--;
	return true;
}

五、查找元素LocateElem_Sq

//查找线性表中的元素
int LocateElem_Sq(SqList L, ElemType e) {
	int i = 1;  //返回下标
	ElemType* p = &L.elem[0];  //从第一个元素开始遍历
	while (i <= L.length && *p++ != e) ++i;  //如果没遍历到头，*p与e不相同，则继续遍历
	if (i <= L.length) return i;
	else return 0;
}

 

六、归并线性表MergeList_Sq

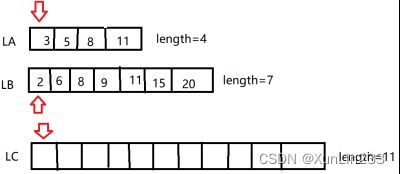
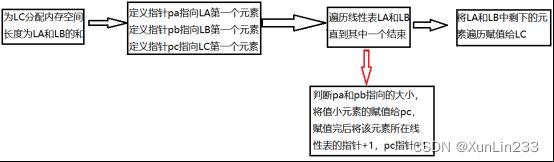
已知线性表LA和LB的数据元素按值非递减有序排列，现要求将LA和LB归并为一个新的线性表LC，且LC中的数据元素仍按值非递减有序排列。

LA=（3,5,8,11） LB=（2,6,8,9,11,15,20）则 LC=（2,3,5,6,8,8,9,11,11,15,20）

分析：

（1）LC的长度为LA和LB长度之和，定义两个指针分别指向LA的第一个元素和LB的第一个元素，还有一个指针指向LC的第一个元素

（2）比较两个元素的大小，将小的值赋值给LC的第一个元素，并将小的元素的线性表的指针和LC的指针右移一位

（3）继续第二步的操作

（4）继续第二步操作

（5）一直到其中一个线性表结束，LB中还剩余两个元素

（6）再将LA和LB中剩下的线性表元素遍历赋值给LC即可

总结：

//归并线性表
void MergeList_Sq(SqList LA, SqList LB, SqList& LC) {
	LC.length = LC.listsize = LA.length + LB.length;  //LC的长度为LA和LB的和
	LC.elem = (ElemType*)malloc(LC.listsize * sizeof(ElemType));  //为LC分配空间
	ElemType* pa = LA.elem;
	ElemType* pb = LB.elem;
	ElemType* pc = LC.elem;
	ElemType* pa_last = &LA.elem[LA.length - 1];
	ElemType* pb_last = &LB.elem[LB.length - 1];
	while (pa <= pa_last && pb <= pb_last) {  //遍历LA和LB
		if (*pa <= *pb) *pc++ = *pa++;  //判断pa和pb指向元素的大小，赋值过后指针向后移动
		else *pc++ = *pb++;
	}
	while (pa <= pa_last) *pc++ = *pa++;  //将剩下的元素赋值给LC
	while (pb <= pb_last) *pc++ = *pb++;
}

 

七、求线性表的并集union_Sq

求并集就是在求并归的基础上加上用LocateElem_Sq函数判断LA和LB中是否有相同的元素，如果LB中有LA中的元素，那么用ListDelete_Sq函数从LA中删除该元素，保证LA中的元素不会与LB中的元素冲突，然后正常使用并归函数即可。

 

//线性表求并集
void union_Sq(SqList LA, SqList LB, SqList& LC) {
	for (int i = 0; i <= LA.length;i++) {  //遍历LA
		if(LocateElem_Sq(LB, LA.elem[i])) ListDelete_Sq(LA,i+1);  //如果该元素在LB中存在，则删除LA中的该元素
	}
	MergeList_Sq(LA, LB, LC);
}