基于内容的图像特征提取系统
随着信息化多媒体时代的到来及世界范围内Internet的发展,人们在工作和生活中越来越多的接触到大量的各种各样的图像信息。图像作为一种重要的信息载体,具有直观、内容丰富、无语言限制和便于国际交流等特点,是组成多媒体信息的重要内容。图像处理技术已经广泛深入的应用于各行各业中。
数据库技术主要研究数据库的结构、设计以及如何进行数据的组织、存储、管理。计算机硬件技术的发展和计算机软件水平的提高,为图像的存储、压缩、传输、交互提供了必要的基础。使得图像处理技术和数据库技术结合成为可能。随着这一研究领域的发展,图像数据库成为当今信息管理的基础。它既充分利用了图像内部所包含的信息,又结合了传统数据库技术,是一项在理论研究和实际应用中都极有前途的新技术。在浩如烟海的信息中,寻找感兴趣的资料是极其耗时的,人们对信息检索和系统的依赖日益加强。传统的政府办公系统已经无法适应快速发展的信息化社会的需求。近年来,多媒体数据库在政府政务信息处理中越来越显示出其快速、便捷的优越性能,受到各国政府的广泛重视。它不是简单的办公自动化、网络化、电子化,而是一个综合的信息系统,它是各有关部门和地方各级政府利用信息和网络通信技术,是加强政府管理,实现政务公开、提高效率、改进和完善服务职能的重要手段。
1.2 国内外研究现状
早在70年代,人们就开始了图像检索技术的研究,实现了基于文本方式的图像检索。典型框架是:首先对图像进行人工标注,然后应用文本检索技术实现对标注图像的检索。这种方法当图像库中的图像数量不大且图像内容比较单一时,不失为一种简单易行的方法。然而,当图像数据量非常庞大时,基于文本的图像检索存在着诸多困难:
首先,手工对图像进行标注所需要的工作量大,效率低;其次,图像内容的复杂多样使得图像注释具有较强的主观性:即使相同的图像,不同的人对图像的理解也不完全一致,存在二义性;另外,对图像而言它不同于文字信息,图像内容本身不能直接进行排序,不能直接进行准确比较,具有难以用符号描述的视觉特征信息,如图像内容的空间关系、图像颜色、纹理、形状等是难以用准确的词汇描述的。由于图像内容的丰富内涵以及人们对图像内容进行抽取的主观性,使得基于文本的方法往往不能准确的检索,不能取得较为满意的效果,这种技术的适用范围及领域受到极大的限制。近年来,一种区别于传统的基于文本的检索手段,被称为基于内容的图像检索技术成为研究的热点。
基于内容的图像检索CBIR(Content Based Image Retrieval),是利用图像内容实现图像检索的一项综合性技术,是指根据图像内容特征以及特征组合,从图像库中直接找到含有特定内容的图像。图像的内容特征包括图像的外观特征(颜色、纹理、形状)和语义。其中,图像的颜色、纹理、形状等外观特征被认为是较低层次上的特征,具有相对直观的特点;而语义是较高层次上的特征,具有相对主观抽象的特点。事实上,图像的内容特征是对图像内容的压缩和抽象,与人类的观察十分相似,因而基于内容的图像检索的检索结果能够满足用户的需要。目前研究和应用的层次主要是采用基于特征的检索方式。基于图像内容实现检索的基本思路是:
首先,通过对图像内容的分析,自动或半自动的提取图像的颜色、纹理、形状、对象的空间关系等特征;然后,建立图像的特征矢量作为其索引,利用基于这些特征定义的相似度量函数计算或评价特征之间的相似性;
最后,将相似的图像作为检索结果返回给用户。在整个的检索过程中,第一步是至关重要的,它关系到以后的各个环节。因此基于内容的图像特征提取的研究是一直以来人们关注的焦点,也是本文研究的重点,将在后面做较详细的分析。
颜色是图像非常重要的视觉特征,是人识别图像的主要感知特征之一。相对于其它特征,颜色特征对于图像的平移、尺度、旋转变化不敏感,具有很强的鲁棒性,而且计算简单。基于这些优点,利用颜色特征进行图像检索因而受到重视,成为基于内容图像检索系统中应用最广泛的主要特征之一。如何准确充分的提取一幅图像的颜色信息,并以适当的方式表示,将直接影响整个图像检索系统的效率和精度。
利用颜色特征进行图像检索的关键之一是颜色特征的提取。图像的颜色特征可以是各种颜色的比例分布以及颜色空间的分布等。本章首先介绍了常用的颜色信息提取和表示方法,其中颜色直方图的方法是目前效果最好、应用最广的方法,HSV颜色模型是一种比RGB颜色模型视觉均匀的模型。本文采用了基于HSV颜色空间的颜色直方图的方法提取图像的颜色特征。分别获得图像的色调、亮度以及饱和度信息,通过加权的方法对图像中的色调、亮度和饱和度进行综合,使得提取的特征更接近人对颜色的视觉感知特性,同时算法对图像的不同分量根据人类的视觉对颜色感知的经验值进行非等间隔量化,有效的压缩了特征矢量的维数,减小了图像特征数据库的大小,提高图像的检索查寻速度。在此基础上针对含有目标的图像,提出了改进的颜色直方图的算法,即加权颜色直方图方法。最后对基于这两种颜色特征值进行图像检索的实验结果进行了比较分析。
在基于内容的图像检索中,颜色是图像非常重要的视觉特征。相对于几何特征而言,颜色具有一定的稳定性,其对大小、方向都不敏感。因而利用颜色特征进行图像检索技术受到重视,并最早得到应用。一般采用直方图来描述图像的颜色特征。计算每幅图像的颜色直方图,即每一种颜色在图像像素点中的比例,作为图像的特征矢量加以保存。
1991年,ML Swain和DH Ballard发表了颜色索引一文,使用颜色直方图求交进行图像颜色相似性计算,迈出了基于内容检索的第一步。颜色的检索一般应用于色彩较为丰富的自然图景的图像检索中。
3.2 基于颜色的特征表达
图像的颜色己经是人们注意的记忆图像的主要特征之一。颜色不像其它信息那样揭示物体本质特性,但是颜色作为图像的特征有其特殊的特点,使得在某些场合下利用颜色进行图像检索有着很高的效率和准确性。在大自然中,颜色经常标志了不同的物种。
在人们的生活中,颜色也常常用来作为警示等标志。颜色作为物体的属性之一用于图像检索系统,具有以下特点:
·数据量小。在这个世界上出现的颜色中,只需要采用两百多种离散的颜色,就可以区分大量的物体。
·颜色特征与图像位移、尺寸和图像中的对象的位置无关,具有位移不变性、旋转不变性和尺寸不变性。
·颜色特征受物体完整性的影响较小。当物体部分的遮挡时,相对于颜色直方图而言,颜色直方图受到的影响不是很大。
·颜色直方图受图像的分辨率的影响较小。
·噪声对检索效果有一定的影响,但通过某种算法很容易减小噪音对匹配工作的影响。
3.3 颜色空间
如何用数值表示纷繁复杂的颜色,人们已经进行了许多研究。研究表明,人眼对颜色的感知是三维的,找到符合人眼视觉特征的颜色模型是利用颜色特征进行图像检索的关键。图像的颜色特征不仅取决于图像本身,而且还与观察者的视觉系统和观察经验有关。因此为了准确提取表征原始图像颜色信息,提取算法必须在符合人类视觉系统的生理特征和人类观察经验的视觉感知特征的颜色空间内进行。对彩色图像颜色特征提取的研究,必须在特定的颜色空间中进行。实际应用中常用到的颜色空间很多,比如L*a*b*颜色空间、RGB空间、HSV空间、Munsell空间、YUV空间等等。
3.3.1 RGB颜色空间
面向硬设备的最常用颜色模型是RGB模型,它是一种与人的视觉系统结构密切相连的模型。根据人眼结构,所有颜色都可看作是3个基本颜色-红R,绿G和蓝B的不同组合。为了建立标准,国际照度委员会(CIE)早在1931年就规定红、绿、蓝这3种基本色的波长分别为700nm,546.lnm,435.8nm。由于光源的光谱是连续渐变的,所以并没有一种颜色可准确地叫做红、绿、蓝。因而需要注意,定义3种基本波长并不表明仅由3个固定的R、G、B分量就可组成所有颜色。
RGB模型可以建立在笛卡儿坐标系统里,其中3个轴分别为R,G,B,见图3-1所示。RGB模型的空间是个正方体,原点对应黑色,离原点最远的顶点对应白色。在这个模型中,从黑到白灰度值分布在从原点到最远顶点间的连线上,而立方体内其余各点对应不同的颜色,可用从原点到该点的向量表示。一般为方便起见,总将立方体归一化为单位立方体,这样所有的R,G,B的值都在区间[0,1]之中。
根据这个模型,每幅彩色图都包括3个独立的基色平面,或者说可分解到3个平面上。反过来,如果1幅图像可被表示为3个平面,使用这个模型比较方便。色觉的产生需要发光光源的光通过反向或透射方式传递到眼睛,刺激视网膜细胞引起神经信号传输到大脑,然后人脑对此加以解释产生色觉。
3.4.1 颜色特征的表征方法
·颜色直方图法
颜色直方图是在许多图像检索系统中被广泛应用的颜色特征,具有很好的表现能力。彩色图像的直方图描述的是不同颜色在整幅图像中所占的比例,而并不关心每种颜色所处的空间位置。颜色直方图特别适用于描述那些难以自动分割的图像和不需要考虑物体空间位置的图像。
·颜色矩表示法
颜色矩(Color Moments)特征是由Stricker和Orengo所提出的。这种方法的数学基础在于图像中任何的颜色分布矩可以用它的矩来表示。由于颜色分布信息主要集中在低阶矩中,因此仅采用颜色的一阶矩(mean)、二阶矩(variance)、三阶矩(skewness)就足以表达图像的颜色分布。图像的颜色矩一共只需九个分量:三个颜色分量,每个分量上三个低阶矩,与其它的颜色特征相比是非常简洁的。但是颜色矩特征的分辨能力较低,一般起到过滤缩小范围的作用,通常和其它特征结合使用。
·颜色集表示法
为支持大规模图像库中的快速查找,Smith和Chang提出了用颜色集(color set)作为对颜色直方图的一种近似。首先将图像从RGB空间转化成视觉均衡的颜色空间中的图像,并将颜色空间量化成若干个bin。然后用色彩自动分割技术将图像分为若干区域,每个区域用量化颜色空间的某个颜色分量来索引,从而将图像表达为一个二进制的颜色索引集。在图像匹配中,比较不同图像颜色集之间的距离和色彩区域的空间关系。因为颜色集表达为二进制的特征向量,可以构造二分查找数来加快速度,这对于大规模的图像库十分有利。但在强调了检索速度的同时,也丧失了查找的准确性。
·颜色对表示法
颜色直方图丢失了颜色的位置信息,因此它对图像的细致查找或对图像中对象的查找不太合适。如果能够借助图像子块之间颜色的邻接关系,通过颜色进行组对建模,则若两幅图像具有相同颜色组对,那么就建立了这两幅图像的相似性描述,不仅是在全局的颜色构成上,而且在局部位置上的颜色构成上。这就是所谓的颜色对方法。
3.4.2 颜色特征提取算法和MATLAB仿真
本文我们主要研究基于HSV的颜色特征提取算法。本文的图像处理我们采用一下的图片进行处理:
图3-4 系统初始处理的图像
HSV颜色空间的每个分量直接对视觉感受起作用,是均匀的颜色空间。HSV模型对应于画家配比模型,它能较好反映人对颜色的感知和鉴别能力,非常适用用于基于颜色的图像相似比较。从人的心理感知来说,HSV颜色空间要比RGB颜色空间更直观,更容易接受。
·MATLAB程序设计与仿真
通过上面的分析,我们可以编写如下的代码,首先H,S,V的计算公式的MATLAB代码如下所示:
H计算公式:
for i = 1:M
for j = 1:N
%第1级
if h(i,j)>345&&h(i,j)<=360||h(i,j)<=15
H(i,j)=0;
end
%第2级
if h(i,j)>15&&h(i,j)<=25
H(i,j)=1;
end
%第3级
if h(i,j)>25&&h(i,j)<=45
H(i,j)=2;
end
%第4级
if h(i,j)>45&&h(i,j)<=55
H(i,j)=3;
end
%第5级
if h(i,j)>55&&h(i,j)<=80
H(i,j)=4;
end
%第6级
if h(i,j)>80&&h(i,j)<=108
H(i,j)=5;
end
%第7级
if h(i,j)>108&&h(i,j)<=140
H(i,j)=6;
end
%第8级
if h(i,j)>140&&h(i,j)<=165
H(i,j)=7;
end
%第9级
if h(i,j)>165&&h(i,j)<=190
H(i,j)=8;
end
%第10级
if h(i,j)>190&&h(i,j)<=220
H(i,j)=9;
end
%第11级
if h(i,j)>220&&h(i,j)<=255
H(i,j)=10;
end
%第12级
if h(i,j)>255&&h(i,j)<=275
H(i,j)=11;
end
%第13级
if h(i,j)>275&&h(i,j)<=290
H(i,j)=12;
end
%第14级
if h(i,j)>290&&h(i,j)<=316
H(i,j)=13;
end
%第15级
if h(i,j)>316&&h(i,j)<=330
H(i,j)=14;
end
%第16级
if h(i,j)>330&&h(i,j)<=345
H(i,j)=15;
end
end
end
S计算公式:
for i=1:M
for j=1:N
%第1级
if s(i,j)>0&&s(i,j)<=0.15
S(i,j)=0;
end
%第2级
if s(i,j)>0.15&&s(i,j)<=0.4
S(i,j)=1;
end
%第3级
if s(i,j)>0.4&&s(i,j)<=0.75
S(i,j)=2;
end
%第4级
if s(i,j)>0.75&&s(i,j)<=1
S(i,j)=3;
end
end
end
V计算公式:
for i=1:M
for j=1:N
%第1级
if v(i,j)>0&&v(i,j)<=0.15
V(i,j)=0;
end
%第2级
if v(i,j)>0.15&&v(i,j)<=0.4
V(i,j)=1;
end
%第3级
if v(i,j)>0.4&&v(i,j)<=0.75
V(i,j)=2;
end
%第4级
if v(i,j)>0.75&&v(i,j)<=1
V(i,j)=3;
end
end
end
L计算公式:
for i=1:M
for j=1:N
if s(i,j)>0.2&&s(i,j)<=1&&v(i,j)>0.2&&v(i,j)<=1
L(i,j)=16*H(i,j)+4*S(i,j)+V(i,j);
end
end
end
其仿真结果如下所示:
图3-5 原始图1的颜色提取效果图
图3-6 原始图2的颜色提取效果图
图3-5是图像1的HSV空间的L联合特征矢量直方图;图3-6是将原图像旋转了180度得到彩色图像2以后求得的其L联合特征矢量直方图,结果与彩色图像1的完全一致,从而验证了HSV空间的L特征矢量直方图同样具有旋转不变性。
图3-7 原始图3的颜色提取效果图
这个说明不同的图像的颜色提取效果是不同的,通过这个仿真结果我们可以区分不同图像。同样道理,对于原始图4其是图3的旋转图,其HSV颜色提取仿真效果和图3-7是也是完全相同的。
4.1纹理特征简介
纹理作为物体的一个重要而又难以描述的特征,也是基于内容检索的一条重要线索。基于纹理的特征提取在区分有相似颜色区域时是非常有用的。各种各样的技术已经被用来计算纹理的相似性,常用的纹理分析方法是统计方法,如基于共生矩阵的纹理分析,基于马尔可夫随机场的纹理分析,基于小波变换的纹理分析方法等。由于纹理分析方法千差万别,因此对不同的应用领域设计不同的纹理分析方法。
数字图像中的纹理是相邻像素的灰度或颜色的空间相关性,或是图像灰度和颜色随空间位置变化的视觉表现,使用数学或信息论的方法抽取的纹理度量称为纹理特征。由于纹理特征可用来对图像中的空间信息进行一定程度的定量描述,因此也是基于内容的图像检索中一个重要手段。
4.2 纹理特征的表征方法
统计法纹理描述方法利用适合于统计模式识别的形式来描述纹理。在每个纹理描述结果中,每个纹理属性用一个特征向量来描述,它代表了多维特征空间中的一个点。它的目标是寻找一个确定型的或者概率型的决策规则给纹理赋予特定的类别。统计法纹理描述主要有共生矩阵,分形理论,国际标准MPEG-7提供的边缘直方图纹理描述符,数学形态学的方法以及基于自相关函数的纹理描述方法等。
·结构分析方法
结构分析方法的基本思想是认为复杂的纹理可由一些简单的纹理基元以一定的有规律的形式重复排列组合而成。如果定义出一些排列基元的规则,就有可能将某些纹理基元按照规定的方式组织成所需要的纹理模式。纹理基元描述了局部纹理特征,对整幅图像中不同纹理基元的分布统计可获得图像的全面纹理信息。对于存在于纹理基元之间的结构关系,可以有不同的分析途径。最简单的方法是分析纹理基元之间存在相位、距离、尺寸等统计特征,也可以考虑用复杂的方法分析,如利用模型或句法等。
·统计分析方法
该方法利用纹理的统计特性和规律来描述纹理,它适用于像木纹、砂地、草坪那样的细而不规则的自然纹理,也同样适用于人工纹理,是最早应用在纹理分析中的方法之一。统计方法从根据像素灰度值的统计分析出发,推导出一些统计量表达纹理特征。根据特征计算时所使用的点的个数,此类方法又可分为一阶统计量、二阶统计量和高阶统计量。
在本章,我们将要仿真的原始图像如下所示:
图4-1 原始图像
我们首先利用颜色提取的方法对图像进行仿真,得到如下的仿真结果:
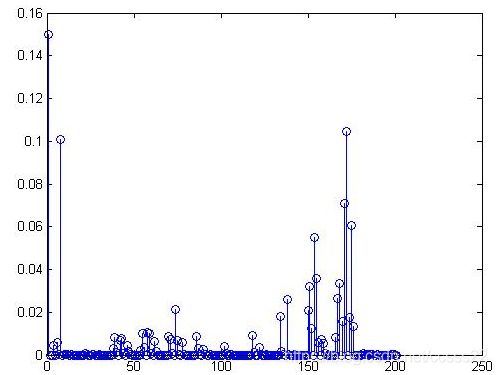
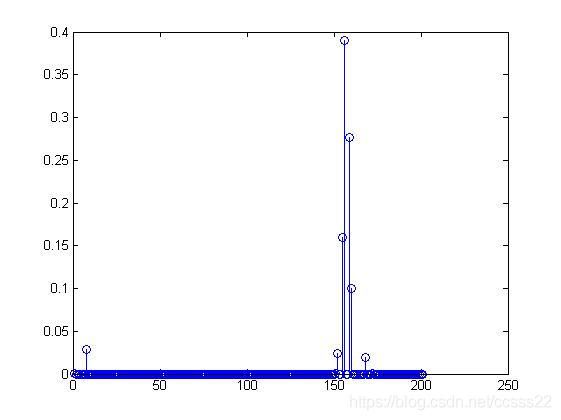
图4-2 颜色提取仿真图
通过仿真我们发现当两个颜色大致相同的时候(这里都为蓝色为主色调),那么通过颜色提取后其结果相似,上图中其峰值都在150左右开始,如果我们要识别的图像颜色更接近,那么其峰值机会相同,这对我们图像的检索造成困难,所以这里我们将对这类图片进行进一步的测试,我们将根据其纹理进行判断。
那么在这种情况下,我们就需要对其纹理进行提取,即在仿真中对于同一点的幅度进行比较,其代码较长,这里我们直接给出仿真结果图:
图4-3 图一的纹理提取仿真结果
我们可以看到其峰值的最值为2多点。
图4-4 图二的纹理提取仿真结果
我们可以看到其峰值的最值为2.5多点。
通过对比就能分析出是不同的图片。
1-颜色特征提取
clc;
clear;
close all;
Image=imread('2.bmp');
[M,N,O]=size(Image);
[h,s,v]=rgb2hsv(Image);
H=h;
S=s;
V=v;
h=h*360;
for i=1:M
for j=1:N
if v(i,j)<0.2
L(i,j)=0;
end
if s(i,j)<0.2&&v(i,j)>0.2&&v(i,j)<=0.8
L(i,j)=(v(i,j)-0.2)*10+1;
end
if s(i,j)<0.2&&v(i,j)>0.8&&v(i,j)<=1
L(i,j)=7;
end
end
end
%*************************************************
% h量化成16级;
% s量化成4级;
% v量化成4级;
for i = 1:M
for j = 1:N
%第1级
if h(i,j)>345&&h(i,j)<=360||h(i,j)<=15
H(i,j)=0;
end
%第2级
if h(i,j)>15&&h(i,j)<=25
H(i,j)=1;
end
%第3级
if h(i,j)>25&&h(i,j)<=45
H(i,j)=2;
end
%第4级
if h(i,j)>45&&h(i,j)<=55
H(i,j)=3;
end
%第5级
if h(i,j)>55&&h(i,j)<=80
H(i,j)=4;
end
%第6级
if h(i,j)>80&&h(i,j)<=108
H(i,j)=5;
end
%第7级
if h(i,j)>108&&h(i,j)<=140
H(i,j)=6;
end
%第8级
if h(i,j)>140&&h(i,j)<=165
H(i,j)=7;
end
%第9级
if h(i,j)>165&&h(i,j)<=190
H(i,j)=8;
end
%第10级
if h(i,j)>190&&h(i,j)<=220
H(i,j)=9;
end
%第11级
if h(i,j)>220&&h(i,j)<=255
H(i,j)=10;
end
%第12级
if h(i,j)>255&&h(i,j)<=275
H(i,j)=11;
end
%第13级
if h(i,j)>275&&h(i,j)<=290
H(i,j)=12;
end
%第14级
if h(i,j)>290&&h(i,j)<=316
H(i,j)=13;
end
%第15级
if h(i,j)>316&&h(i,j)<=330
H(i,j)=14;
end
%第16级
if h(i,j)>330&&h(i,j)<=345
H(i,j)=15;
end
end
end
for i=1:M
for j=1:N
%第1级
if s(i,j)>0&&s(i,j)<=0.15
S(i,j)=0;
end
%第2级
if s(i,j)>0.15&&s(i,j)<=0.4
S(i,j)=1;
end
%第3级
if s(i,j)>0.4&&s(i,j)<=0.75
S(i,j)=2;
end
%第4级
if s(i,j)>0.75&&s(i,j)<=1
S(i,j)=3;
end
end
end
for i=1:M
for j=1:N
%第1级
if v(i,j)>0&&v(i,j)<=0.15
V(i,j)=0;
end
%第2级
if v(i,j)>0.15&&v(i,j)<=0.4
V(i,j)=1;
end
%第3级
if v(i,j)>0.4&&v(i,j)<=0.75
V(i,j)=2;
end
%第4级
if v(i,j)>0.75&&v(i,j)<=1
V(i,j)=3;
end
end
end
%将三个颜色分量合成为一维特征向量
for i=1:M
for j=1:N
if s(i,j)>0.2&&s(i,j)<=1&&v(i,j)>0.2&&v(i,j)<=1
L(i,j)=16*H(i,j)+4*S(i,j)+V(i,j);
end
end
end
%计算L的直方图
for i=0:200
Hist(i+1)=size(find(L==i),1);
end
Hist = Hist/sum(Hist)
i=0:1:200
figure,stem(i+1,Hist(i+1));
2-纹理提取
clc;
clear;
close all
IN=imread('2.bmp');
gray=256;
[R,C]=size(IN);
%采用平方求和计算梯度矩阵
GM=zeros(R-1,C-1);
for i=1:R-1
for j=1:C-1
n_GM=(IN(i,j+1)-IN(i,j))^2+(IN(i+1,j)-IN(i,j))^2;
GM(i,j)=sqrt(double(n_GM));
end
end
% figure,imshow(GM);
%找出最大值最小值
n_min=min(GM(:));
n_max=max(GM(:));
%把梯度图象灰度级离散化
new_gray=32;
%新的梯度矩阵为new_GM
new_GM=zeros(R-1,C-1);
new_GM=uint8((GM-n_min)/(n_max-n_min)*(new_gray-1));
%计算灰度梯度共生矩阵
%梯度矩阵比轨度矩阵维数少1,忽略灰度矩阵最外围
H=zeros(gray,new_gray);
for i=1:R-1
for j=1:C-1
H(IN(i,j)+1,new_GM(i,j)+1)= H(IN(i,j)+1,new_GM(i,j)+1)+1;
end
end
%归一化灰度梯度矩阵 H_basic
total=i*j;
H_basic=H/total;
%小梯度优势 T1
TT=sum(H);
T1=0;
for j=1:new_gray
T1=T1+TT(1,j)/j^2;
end
T1=T1/total;
%计算大梯度优势 T2
T2=0;
for j=1:new_gray
T2=T2+TT(1,j)*(j-1);
end
T2=T2/total;
%计算灰度分布的不均匀性 T3
T3=0;
TT1=sum(H');
for j=1:gray
T3=T3+TT1(1,j)^2;
end
T3=T3/total;
%计算梯度分布的不均匀性 T4
T4=0;
for j=1:new_gray
T4=T4+TT(1,j)^2;
end
T4=T4/total;
%计算能量 T5
T5=0;
for i=1:gray
for j=1:new_gray
T5=T5+H_basic(i,j)^2;
end
end
%计算灰度平均 T6
TT2=sum((H_basic)');
T6=0;
for j=1:gray
T6=T6+(j-1)*TT2(1,j);
end
%计算梯度平均 T7
T7=0;
TT3=sum(H_basic);
for j=1:new_gray
T7=T7+(j-1)*TT3(1,j);
end
%计算灰度均方差 T8
T8=0;
for j=1:gray
T8=T8+(j-1-T6)^2*TT2(1,j);
end
T8=sqrt(T8);
%计算梯度均方差 T9
T9=0;
for j=1:new_gray
T9=T9+(j-1-T7)^2*TT3(1,j);
end
T9=sqrt(T9);
% 计算相关 T10
T10=0;
for i=1:gray
for j=1:new_gray
T10=T10+(i-1-T6)*(j-1-T7)*H_basic(i,j);
end
end
%计算灰度熵 T11
T11=0;
for j=1:gray
T11=T11+TT2(1,j)*log10(TT2(1,j)+eps);
end
T11=-T11;
%计算梯度熵 T12
T12=0;
for j=1:new_gray
T12=T12+TT3(1,j)*log10(TT3(1,j)+eps);
end
T12=-T12;
%计算混合熵 T13
T13=0;
for i=1:gray
for j=1:new_gray
T13=T13+H_basic(i,j)*log10(H_basic(i,j)+eps);
end
end
T13=-T13;
%计算惯性 T14
T14=0;
for i=1:gray
for j=1:new_gray
T14=T14+(i-j)^2*H_basic(i,j);
end
end
%计算逆差矩 T15
T15=0;
for i=1:gray
for j=1:new_gray
T15=T15+H_basic(i,j)/(1+(i-j)^2);
end
end
x=1:50:750;
OUT(1,1)=T1;
OUT(1,2)=T2;
OUT(1,3)=T3;
OUT(1,4)=T4;
OUT(1,5)=T5;
OUT(1,6)=T6;
OUT(1,7)=T7;
OUT(1,8)=T8;
OUT(1,9)=T9;
OUT(1,10)=T10;
OUT(1,11)=T11;
OUT(1,12)=T12;
OUT(1,13)=T13;
OUT(1,14)=T14;
OUT(1,15)=T15;
for num=1:15
if num>2
stem(x,OUT,'-');
hold on;
else
stem(x,OUT,'-*r');
hold on;
end
end