基础算法—

目录

快速排序（​编辑）

归并排序（​编辑）

二分法o(logn)

高精度整数计算（BigInteger）

前缀和、差分

前缀和矩阵

差分矩阵

双指针算法

最长连续不重复字符串

数组元素目的和

判断在子序列

位运算

离散化

区间和并

哈希表

---

快速排序（）

快排三要素：取值、换位、递归

临界点误判易造成死循环：当取数组判定点时，若取到最小、唯一、在最左：左右指针指向最左，左侧递归调用方法时传参右指针为i-1/j-1，成为(q,0,-1)，右侧递归参数为(q,0,r)和原递归参数值一样，无限循环。
    若取到最大、唯一、在最右：左右指针指向最右。。。

解决：当取左侧时，左递归传有参数为i或j,(q,l,i)
           取右侧时，左递归参数i-1或j-1,(q,l,i-1)

AcWing785 快速排序

    public static void quick_sort(int q[],int l,int r){
        if(l>=r) return;
        
        int mid = q[l], i = l - 1, j = r + 1;
        while(i < j){
            while(q[++i] < mid);
            while(q[--j] > mid);
            if(i < j){
                int t = q[i];
                q[i] = q[j];
                q[j] = t;
            }
        }
        
        quick_sort(q,l,j);
        quick_sort(q,j+1,r);
    }

归并排序（）

1.找到区间中点mid
2.将[l,mid]和[mid+1,r]排好序
3.将[l,mid]和[mid+1,r]合并

AcWing187归并排序

合并时大体看成两个两个已经排好序的数组，比较拿出最小的，如剩下一方则的全部依次拿出赋值。 其实递归到叶子节点（下左）只有两个数据拿出第一个while循环最小的，其余两个while循环拿出剩下那个。 

    public static void mergeSort(int l,int r){
        if(l>=r) return;
        int mid = l + r >> 1;
        int i = l, j = mid + 1,k = 0;
        mergeSort(i,mid);
        mergeSort(j,r);
        
        while(i <= mid && j <= r){
            if(number[i] < number[j]) q[k++] = number[i++];
            else q[k++] = number[j++];
        }
        while(i <= mid) q[k++] = number[i++];
        while(j <= r) q[k++] = number[j++];
        
        int p = 0;
        while(l <= r) number[l++] = q[p++];
        
    }

二分法o(logn)

具备单调性一定能二分，不具备单调性部分能二分。

用中点比较判断要找的值在那一段，然后继续二分直到只有一个数时（l = r =1），这时这个数与要找目的值可能相等（接近）。

临界值判定：当只有3个数时，假设下列代码中不加一使得mid取值为 1 , 若符合条件 a[mid] <= x[j]，那么 l = mid  = 1，将陷入死循环。

while(l < r){
                    int mid = l + r + 1 >> 1; // +1避免造成死循环
                    if(a[mid] <= x[j]) l = mid;
                    else r = mid - 1;
                }

高精度整数计算（BigInteger）

高精度的整数计算，如6位数以上的加减乘除很容易超过整数的范围，解决方法：将数字放入字符串中采用10进制单个计算然后再输出结果，当然这里要将数字倒放（个位放在字符串的第0位），避免因位数变化（如5位数变成6位数）而造成整体后移。

在java中直接调用BigInteger即可解决，非常方便，常用方法如下：

BigInteger num1 = new BigInteger(in.readLine());
BigInteger num2 = new BigInteger(in.readLine());

BigInteger add = num1.add(num2);                //加法
BigInteger subtract = num1.subtract(num2);      //减法
BigInteger multiply = num1.multiply(num2);      //乘法
BigInteger divide = num1.divide(num2);          // 除法
BigInteger []bigInteger = num1.divideAndRemainder(num2); //除法求余，第一个是商，第二个是余数
BigInteger max = num1.max(num2);                //返回两者中大的
BigInteger min = num1.min(num2);                //返回两者中小的

前缀和、差分

类似于数列An和数列的和Sn的关系，所给数组 a[0] ~a[n],

前缀和是Sn = a1 + a2 + a3 + ...+ an，差分是 an = b1 + b2 + b3 + ...+ bn。

Sn 、an 、bn 前者是后者的前缀和，后者是前者的差分

s[i+1] = a[i] + s[i]; s[0]初始值为0，求数列an 到 ax之前的和，直接用Sn - S(x-1),非常简便AcWing795 前缀和

当差分中第 i 个值（0开始）增加或减少 C，那么数组 a 从 i 个值开始，后面全增加或减少C。通常用于数组中多段值改变。

初始化：b[i] = a[i]- a[i-1] ，增加某一段（l 到 r ）的数值：b[l] + c，b[r+1] + c，因为 a[r] = a[r-1] + b[r]

Acwing797 差分

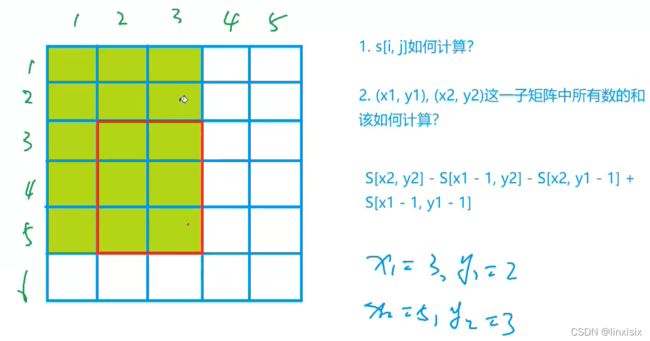
前缀和矩阵

acwing796 求子矩阵

S[x,y]这个点的值就等于原矩阵这个点到左上角所有值的和。

构造前缀和矩阵： 全局静态变量初始值都为0，而数组下标从0开始，所以我们传入值从 1 开始，第0行，0列数值都为0，s[x][y] = s[x][y-1] + s[x-1][y] - s[x-1][y-1] + a[x]]y];

定义两个矩阵所有值都为0则他们就是矩阵前缀和矩阵的关系，然后将赋值看作改变原矩阵中的值去调用方法，当赋值结束时，前缀和矩阵构造完成）

计算原矩阵的子矩阵的和：红框矩阵值，s[x2][y2] - s[x2][y1-1] -s[x1-1][y2] + s[x1-1][y1-1];

差分矩阵

AcWing789 差分矩阵

差分矩阵中若其中某个点数值增加 C，则原矩阵从该点到右下角所有的点全部增加C

如想让原矩阵(x1,y1) 到(x2,y2) 中的数增加 C, 做数学运算即可，让差分矩阵红点加C，黄点右边第一个点减C，绿点下面的第一个减C，黑点右下角第一个加C。

    构造差分数组
    static void insert(int x1, int y1, int x2, int y2, int c){
        bb[x1][y1] += c;
        bb[x1][y2+1] -= c;
        bb[x1+1][y1] -= c;
        bb[x1+1][y1+1] += c;
    }

差分矩阵的构造： 我们假设原矩阵a[N][N]里面所有的值都为0，那么差分矩阵里面的值也全部都是0，现在差分数组已经构成，当我们在向原矩阵赋值时，调用上面的方法（核心为上面四个步骤），当赋值完成，差分矩阵也就构造完成了。

通过差分矩阵的求原矩阵 ：原矩阵就是差分矩阵的前缀和

    //通过差分矩阵的求原矩阵(就是求前缀和)
    static int result(int i, int j){
        bb[i][j] += bb[i-1][j] + bb[i][j-1] - bb[i-1][j-1];
        return bb[i][j];
    }

双指针算法

最长连续不重复字符串

AcWing799 最长连续不重复字符串

暴力破解： i，j 初始指向数组起点，当i向后移动一位时，j遍历一遍从当前位置 j 到 i 是否有a[j] = a[i],若没有则继续，若有则r =max(r, i - j +1), 赋值 j = i,之后继续循环直到i == n。最长连续不重复的字符串长度为 r。

数字

利用数组特性：第一步赋值给 a[]，第二步让 a[i] 当前这个值作为 S[] 的下标，s[a[i]] 存放的是当前a[i] 在目前 j 至 i 中 每一个数字的个数，第三步判断若 a[i]的个数超过了 1，则循环减去 i 到 j 之间的数字的个数（ j 指针向右移动），直至 a[i] 的个数等于1，

for(int i = 0, j = 0; i < n; i ++){
    a[i] = Integer.parseInt(str[i]);
    ++s[a[i]];
    while(s[a[i]] > 1)  --s[a[j++]];
    r = max(r , i -j +1);
}

字符 无重复字符的最长子串

class Solution {
    public int lengthOfLongestSubstring(String s) {
        int  n = s.length(),MAX = 0, start = 0;
        Map map = new HashMap<>();

        for(int end = 0; end < n; end++){
            char c = s.charAt(end);
            if(map.containsKey(c)){
                start =  Math.max(start, map.get(c) + 1); //切换到重复字符下一位， max函数防止切换到之前字符（abba的第一个a）
            } 
            map.put(c,end);//存储索引
            MAX = Math.max(MAX, end - start + 1); // 更新最大不重复字符串
        }

        return MAX;
    }
}

数组元素目的和

AcWing800数组元素目的和
给定Ａ、Ｂ数组，指定ｘ为ＡＢ数组中两个唯一元素的和，求这两个元素的下标ｉｊ。

暴力破解：两个for循环遍历ＡＢ，就能找出，时间负责复杂度为ｎ＾２。

双指针：第一层循环 i从头开始遍历，第二层循环 j从尾向前遍历，第二层循环条件a[i] + b[j] > x，当跳出二层循环时，先判断是否等于 x这个值，是break，不是 i向右移一次，继续二层循环，若最终没有j 先跳出循环为 -1.

        for(int i = 0; i < n; i ++){
            while(Integer.parseInt(a[i]) + Integer.parseInt(b[j]) > x) j--;
            if(Integer.parseInt(a[i]) + Integer.parseInt(b[j]) == x){
                System.out.print(i+" "+j);
                break;
            } 
        }

判断在子序列

AcWing2816 判断在子序列

按顺序，A数组中的值在B数组中都能找到对应匹配的值。

判断是子序列的条件是 i == n

        while(i < n && j < m){
            if(a[i].equals(b[j])) i ++;
            j ++;
        }

位运算

AcWing801位运算   假设数字 N = 10，二进制表示为 (1010)2，

查看个位数的值： N & 1

将数字 N 中的第 k 位 移动到最后一位：N >> k，

两者联合查看第 k 位的数值：N >> k & 1

lowbit操作：x & -x ,返回 x 最后一位1后面的二进制数，包含1

            while (x > 0) {
                count++;
                x -= (x & -x);
            }

离散化

AcWing802区间和

优质题解区间和题解

多次在数轴不同位置x上加c（变化），查询多个区间 [l , r]的和

离散化的本质是映射，将间隔很大的点，映射到相邻的数组元素中。减少对空间的需求，也减少计算量。 最难的就是原数轴的下标在新数组中的位置

开辟三个List集合：addList（存放增加操作），queryList（存放查询操作），indexList（存放下标）

难理解：将数轴上的下标存放在集合 indexList 中，创建和 indexList  “形状相同的数组” ，他们俩的下标相同、但是下标对应的值不同，如上图。增加操作、求区间都需要利用以上关系。

解题思想：将所有的下标（x，l，r）存放到indexList ，排序，去重。创建一个方法find：传入数轴的下标，返回映射在 indexList 的下标。声明两个数组 a[N] ,s[N]，实现所有增加操作,调用find方法给那个a[x]增加 c。之后通过 indexList 的边界值作为循环条件完成前缀和，最后实现查询方法，调用find获取映射在”数组“的下标，利用前缀和 s[r] - s[l-1] 得结果。

    //去重方法
    static int unique(List list){
        int j = 0;
        for(int i = 0; i < list.size();i ++){
            if(i == 0 || list.get(i) != list.get(i-1)){
                list.set(j,list.get(i));
                j++;
            }
        }
        return j;
    }
    //返回原数轴上的下标对应的新数组的下标
    static int find(int x, List list){ //传入的都是indexList
        int l = 0, r = list.size() - 1;
        //利用二分法进行查找
        while(l < r){
            int mid = l + r + 1 >> 1;
            if(list.get(mid) <= x) l = mid;
            else r = mid - 1;
        }
        return l + 1; //为了前缀和设s[0] = 0
    }

区间和并

两区间有三种情况：包含、相交、“相离”。包含不需要进行操作。

我们将所有读取的区间数实例化对象存入ArrayList集合中，通过list.sort()方法对左端点进行排序

        list.sort(new Comparator() {
            public int compare(Pair o1, Pair o2) {
                return o1.getFirst() - o2.getFirst();
            }
        });

初始声明左右端点：

 int sta = (int)-2e9, end = (int)-2e9; //左右边界

计算区间数量：

for(Pair pair : list){
    if(end < pair.getFirst()){  //当前区间的最大值 小于 下一区间的最小，即出现新区间，无法合并
           end = pair.getSecond();
           start = pair.getFirst();
           count++;
    }else{
           end = Math.max(end,pair.getSecond()); //区间合并更新右端点
}
        

哈希表

可以用来快速查询，形式，简单实用是通过Map和HashMap实现

力扣217 存在重复元素

    public boolean containsDuplicate(int[] nums) {
        int n = nums.length;
        Map map = new HashMap<>();
        for(int i = 0; i < n; i ++){
            if(map.get(nums[i]) != null) return true;
            map.put(nums[i],nums[i]);
        }
        return false;
    }