力扣刷题集锦
力扣刷题
- 一、HOT100
-
- (一) 数组
-
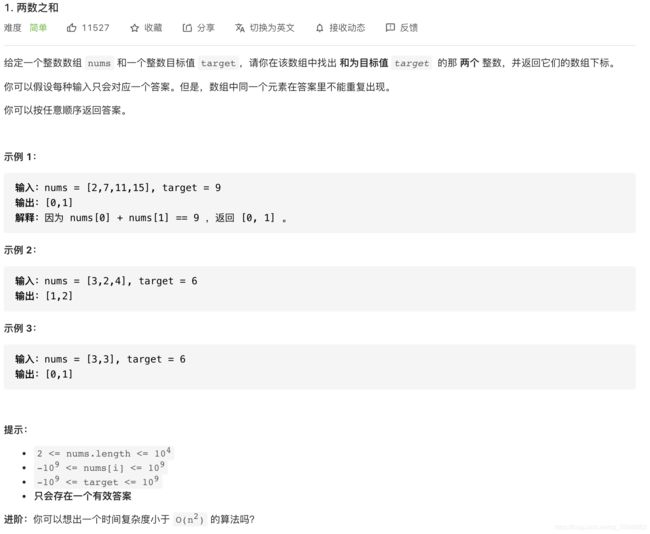
- 1.两数之和
- 4.寻找两个正序数组的中位数
- (二)链表
-
- 2.两数相加
- 19.删除链表的倒数第N个结点
- 21.合并两个有序链表
- (三) 字符串
-
- 3.无重复字符的最长子串
- 20.有效的括号
- (四) 回溯
-
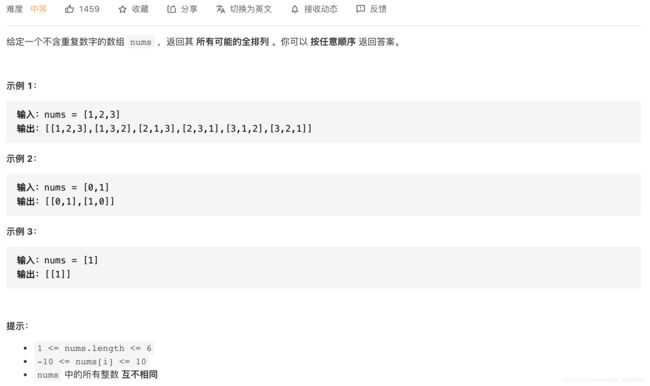
- 46.全排列
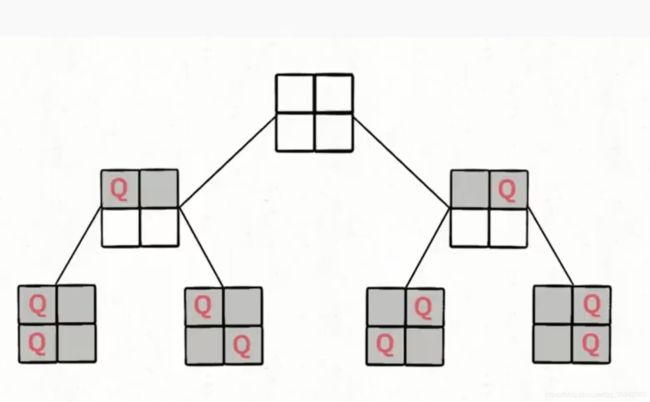
- 51.N皇后
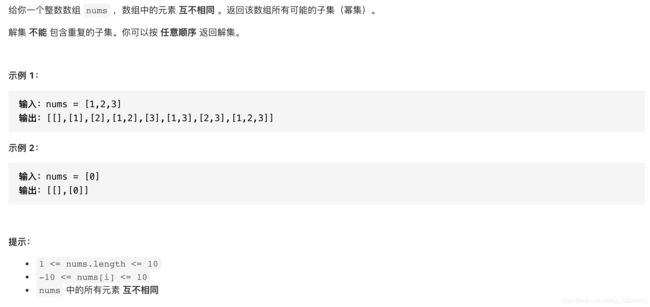
- 78.子集
一、HOT100
(一) 数组
1.两数之和
方法一:暴力
确定左起点之后遍历右边所有节点,当满足两个节点之和等于target时返回结果。
class Solution {
public int[] twoSum(int[] nums, int target) {
int len = nums.length;
int[] result = new int[2];
for (int i = 0; i < len; i++) {
for (int j = i + 1; j < len; j++){
if (nums[i] + nums[j] == target) {
result[0] = i;
result[1] = j;
return result;
}
}
}
return result;
}
}
时间复杂度:O(N^2)
空间复杂度:O(1)
方法二:哈希表
一次遍历数组,期间使用哈希表记录遍历过的节点,然后同时判断当前节点和历史节点之和是否等于targe,等于就返回结果。
class Solution {
public int[] twoSum(int[] nums, int target) {
HashMap<Integer,Integer>map=new HashMap<>();
int[] res=new int[2];
if(nums==null||nums.length==0)return res;
for(int i=0;i<nums.length;i++){
if(map.containsKey(target-nums[i])){
res[0]=i;
res[1]=map.get(target-nums[i]);
}
//判断之后put防止添加自己
map.put(nums[i],i);
}
return res;
}
}
⚠️:哈希表添加元素放在判断之后,因为如果放在之前,会导致一个元素在一次循环中被访问两次。反面示例:【3,2,4】
时间复杂度:O(N)
空间复杂度:O(N)
4.寻找两个正序数组的中位数
(二)链表
2.两数相加

方法一:模拟法
因为链表是倒序的,所以可以直接遍历节点进行相加运算,每计算1个节点就存到结果链表中。
期间注意进位对循环的作用。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
//哑节点记录结果链表头节点位置
ListNode dummy = new ListNode(-1);
ListNode head = dummy;
int c = 0;
int value = 0;
//停止相加的条件是两个链表为空且进位为0
while (l1 != null || l2 != null || c != 0) {
//提前判断空,确定加的数
int x = l1 == null ? 0 : l1.val;
int y = l2 == null ? 0 : l2.val;
//加法过程
value = x + y + c;
c = value / 10;
//更新结果链表
head.next = new ListNode(value % 10);
head = head.next;
//更新l1和l2
if (l1 != null) {
l1 = l1.next;
}
if (l2 != null) {
l2 = l2.next;
}
}
return dummy.next;
}
}
时间复杂度:O(max(m,n))
空间复杂度:O(1) //⚠️结果空间不计入复杂度
19.删除链表的倒数第N个结点
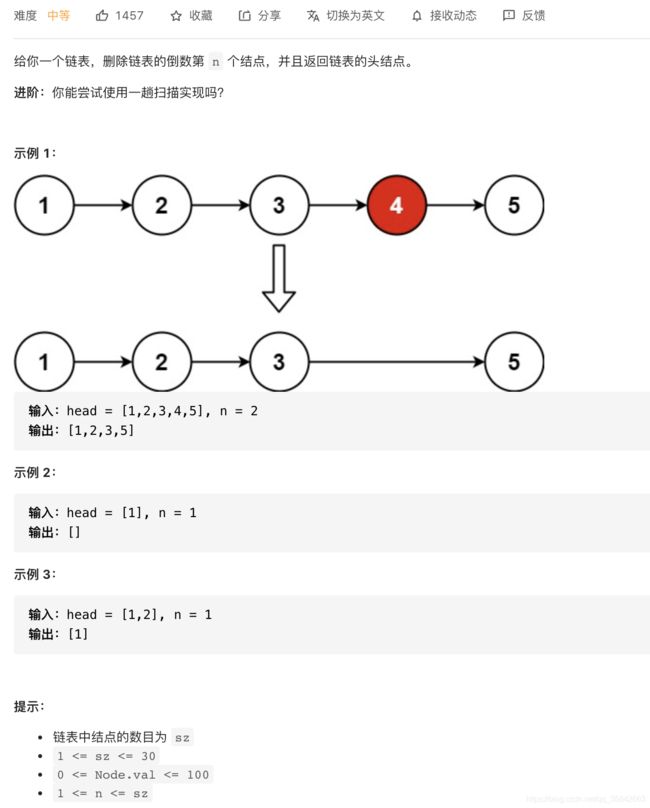
方法一:堆栈
因为题目要求的是删除倒数第n个节点,所以自然想到堆栈,出栈的时候记录删除节点的前后节点,然后改变指向即可,不过要注意删除头节点的情况。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
//创建哑节点
ListNode dummy = new ListNode(-1, head);
Deque<ListNode> stack = new LinkedList<>();
//压栈为了后面的倒序
while (head != null) {
stack.offerFirst(head);
head = head.next;
}
//删除节点的前一个节点
ListNode pre = null;
//删除节点的后一个节点
ListNode post = null;
//记录删除节点的前后节点
for (int i = 1; i <= (n+1); i++) {
ListNode tmp = stack.pollFirst();
if (i == (n-1)) {
post = tmp;
}
if (i == (n+1)) {
pre = tmp;
}
}
//如果pre为null,说明删除的是头节点,直接指向后面一个节点(当整个链表只有一个节点的时候为null)
if (pre == null) {
dummy.next = post;
} else {
pre.next = post;
}
//返回结果
return dummy.next;
}
}
时间复杂度:O(N)
空间复杂度:O(N)
可以改进下:
哑节点主要有两个作用:
- 记录头节点的位置用于结果返回
- 哑节点不在原始链表范围内,可以避免涉及到头节点时一系列的空节点判断
上面的解题过程,第二个优点没有用到,最后还要去判断前继结点是否为null,那其实原链表最多删去头节点,而头节点的前继节点是哑节点,不为空,所以可以把哑节点压栈,要删除的节点出栈后,栈顶就是前继节点,直接原地修改指向就行。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
//创建哑节点
ListNode dummy = new ListNode(-1, head);
Deque<ListNode> stack = new LinkedList<>();
//从哑节点开始遍历可以避免判断删除头节点的情况
ListNode curNode = dummy;
//压栈为了后面的倒序
while (curNode != null) {
stack.offerFirst(curNode);
curNode = curNode.next;
}
//弹出删除结点停止
for (int i = 1; i <= n; i++) {
stack.pollFirst();
}
//找到前一个节点
ListNode prev = stack.peekFirst();
//此时压哑节点入栈的优点就体现了,prev不可能为null,因为n不可能到达哑节点的位置
//更改指向
prev.next = prev.next.next;
//返回结果
return dummy.next;
}
}
时间复杂度:O(N)
空间复杂度:O(N)
方法二:双指针
快慢指针先保持n个间隔,然后同时移动,当快指针到达尾部时,慢指针位于删除节点的前继节点。注意哑节点的作用(快慢指针从哑节点开始)
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
//创建哑节点
ListNode dummy = new ListNode(-1, head);
//创建快慢指针,从哑节点开始为了避免删除头节点时不必要的空判断
ListNode fast = dummy;
ListNode slow = dummy;
//快指针先移动n位
int cnt = 0;
while ((cnt++) < n) {
fast = fast.next;
}
//当快指针指向null时代表到链表尾部了,此时slow处于删除节点的前继
while (fast.next != null) {
fast = fast.next;
slow = slow.next;
}
//前继指向后继
slow.next = slow.next.next;
//返回结果
return dummy.next;
}
}
时间复杂度:O(N)
空间复杂度:O(1)
方法三:递归
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
private int k = 0;
public ListNode removeNthFromEnd(ListNode head, int n) {
if (head == null) {
return null;
}
head.next = removeNthFromEnd(head.next, n);
if ((++k) == n) {
return head.next;
}
return head;
}
}
时间复杂度:O(N)
空间复杂度:O(N)
21.合并两个有序链表
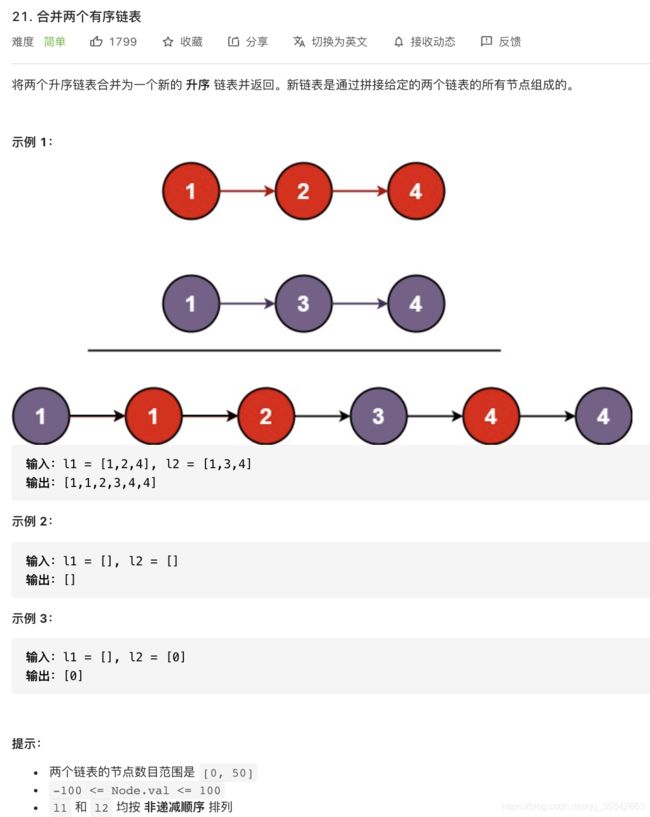
方法一:迭代
遍历两个链表的每个节点,每次结果链表指向较小的节点,最后指向不为null的链表。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
//创建哑节点
ListNode dummy = new ListNode(-1);
ListNode head = dummy;
//只要有一个为null就退出循环
while (l1 != null && l2 != null) {
if (l1.val < l2.val) {
head.next = l1;
l1 = l1.next;
} else {
head.next = l2;
l2 = l2.next;
}
head = head.next;
}
//结果链表接上不为null的链表
if (l1 == null) {
head.next = l2;
}
if (l2 == null) {
head.next = l1;
}
//返回结果
return dummy.next;
}
}
时间复杂度:O(m+n)
空间复杂度:O(1)
方法二:递归法
可以提炼出一个子问题:合并(L1, L2)等价于L1 -> next = 合并(L1 -> next, L2) (l1.val < l2.val)
子问题和原问题具有相同结构,所以可以自上而下地进行递归,结束条件是有一个链表为空。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if (l1 == null) {
return l2;
} else if (l2 == null) {
return l1;
} else if (l1.val <= l2.val) {
l1.next = mergeTwoLists(l1.next, l2);
return l1;
} else if (l1.val > l2.val) {
l2.next = mergeTwoLists(l1, l2.next);
return l2;
}
return null;
}
}
时间复杂度:O(m+n)
空间复杂度:O(m+n)
(三) 字符串
3.无重复字符的最长子串
刚开始这些写的:
class Solution {
public int lengthOfLongestSubstring(String s) {
if (s.length() == 0) {
return 0;
}
int result = 0;
int len = s.length();
//记录字符出现的最新位置
Map<Character, Integer> indexMap = new HashMap<>();
char[] chs = s.toCharArray();
for (int i = 0; i < len; i++) {
int index = indexMap.getOrDefault(chs[i],-1);
if ((i - index) > result) {
result = i - index;
}
indexMap.put(chs[i], i);
}
return result;
}
}
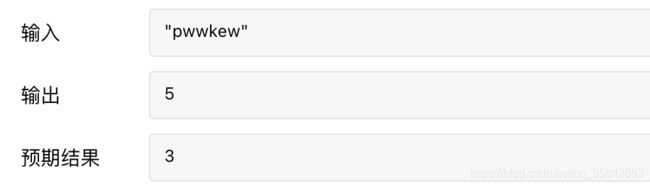
这样肯定不对的,题目要求的是最长子串,而我这是记录字符串中每一位字符的不重复索引的最大值。
主体解题思想应该是记录子字符串的起始位置,当右指针遇到相同的字符时更新起始位置。
可以计算出每个字符作为字符串末尾时的子字符串长度,最后选择最大的,这样可以使用dp,因为以后一个字符结尾的子字符串长度依赖于前一个子串长度
dp[j]定义为以索引j的字符为结尾的不重复的子串的长度,只不过需要分三种情况:
- dp[j] = dp[j-1] + 1, j - i > dp[j-1] 该位置j结尾的子串还没有出现重复字符
- dp[j] = j - i, j - i < dp[j-1] 该位置j结尾的子串出现重复字符
- dp[j] = j - i, j - i = dp[j-1] 该位置j结尾的字符和位置i的字符重复了
i, j 分别记录位置j字符的最新索引。
下面这个讲的更好,区间比较概念更易懂:

方法一:动态规划
class Solution {
public int lengthOfLongestSubstring(String s) {
//判断特殊情况
if (s.length() == 0) {
return 0;
}
//创建返回结果,注意至少为1
int result = 1;
//创建dp数组和初始化
int len = s.length();
char[] chs = s.toCharArray();
int[] dp = new int[len];
dp[0] = 1;
//记录字符出现的最新索引
Map<Character, Integer> indexMap = new HashMap<>();
indexMap.put(chs[0], 0);
//函数主体:遍历字符串
for (int rightIndex = 1; rightIndex < len; rightIndex++) {
//获得当前字符的最新索引
int leftIndex = indexMap.getOrDefault(chs[rightIndex],-1);
//计算该字符的左右索引之差
int diff = rightIndex - leftIndex;
//dp主体
if (diff > dp[rightIndex - 1]) {
dp[rightIndex] = dp[rightIndex - 1] + 1;
}
else if (diff <= dp[rightIndex - 1]) {
dp[rightIndex] = diff;
}
//更新字符索引
indexMap.put(chs[rightIndex], rightIndex);
//更新最大子串长度
if (dp[rightIndex] > result) {
result = dp[rightIndex];
}
}
//返回结果
return result;
}
}
时间复杂度:O(n)
空间复杂度:O(1)//⚠️字符的 ASCII 码范围为 0 ~ 127,哈希表最多使用 O(128) = O(1)大小的额外空间。
map的作用主要是获取当前字符的左边界,所以也可以用循环线性查找:
class Solution {
public int lengthOfLongestSubstring(String s) {
//判断特殊情况
if (s.length() == 0) {
return 0;
}
//创建返回结果,注意至少为1
int result = 1;
//创建dp数组和初始化
int len = s.length();
char[] chs = s.toCharArray();
int[] dp = new int[len];
dp[0] = 1;
//函数主体:遍历字符串
for (int rightIndex = 1; rightIndex < len; rightIndex++) {
//获得当前字符的最新索引
int leftIndex = rightIndex - 1;
while (leftIndex >= 0) {
if (chs[leftIndex] == chs[rightIndex]) {
break;
}
leftIndex--;
}
//计算该字符的左右索引之差
int diff = rightIndex - leftIndex;
//dp主体
if (diff > dp[rightIndex - 1]) {
dp[rightIndex] = dp[rightIndex - 1] + 1;
}
else if (diff <= dp[rightIndex - 1]) {
dp[rightIndex] = diff;
}
//更新最大子串长度
if (dp[rightIndex] > result) {
result = dp[rightIndex];
}
}
//返回结果
return result;
}
}
方法二:双指针
滑动窗口思想:左右指针控制窗口大小。
- 固定左边界时,当右边界的下一个值不超过len且窗口内不包含该元素时就更新右边界,然后更新长度;
- 左边界更新时记得窗口移除上一个左边界元素。
class Solution {
public int lengthOfLongestSubstring(String s) {
//判断特殊情况
if (s.length() == 0) {
return 0;
}
//初始化
int len = s.length();
char[] chs = s.toCharArray();
//右边界初始为-1
int right = -1;
//返回结果至少为1
int result = 1;
//滑动窗口内的元素集合
Set<Character> set = new HashSet<>();
//函数主体
for (int left = 0; left < len; left++) {
//左边界加1 -> 上一个左边界字符删除
if (left != 0) {
set.remove(chs[left - 1]);
}
//当前右边界没超 && 当前滑动窗口内没有右边界元素
//+1是因为初始为-1,字符本身也要计算
while ( (right+1) < len && !set.contains(chs[right+1])) {
set.add(chs[right+1]);
right++;
}
//更新结果
result = Math.max(result, right - left + 1);
}
//返回结果
return result;
}
}
时间复杂度:O(n)
空间复杂度:O(1)
20.有效的括号
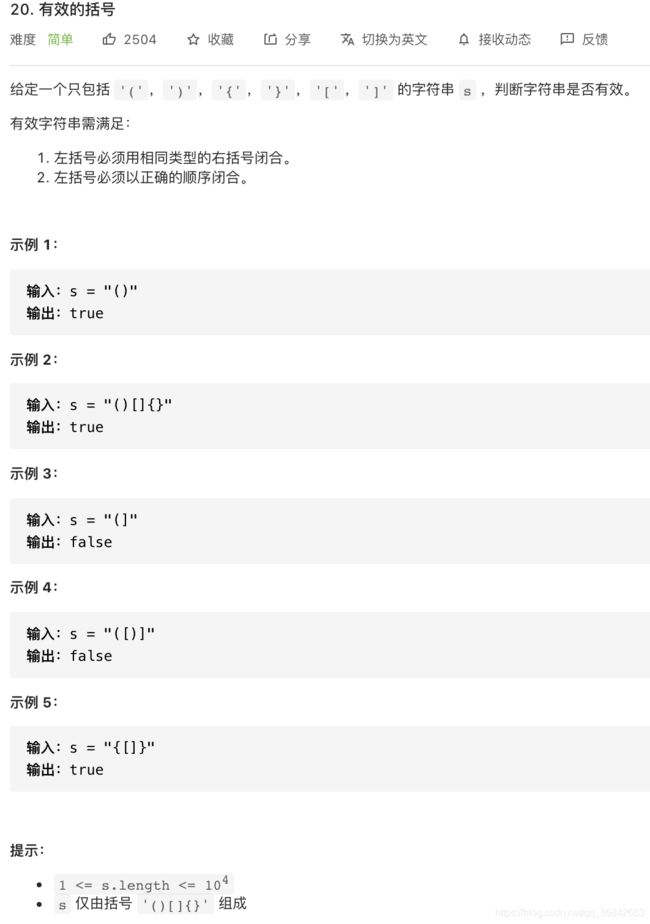
堆栈法:
栈顶元素和字符元素不匹配就压栈,否则就出栈,最后判断栈空。
class Solution {
public boolean isValid(String s) {
int len = s.length();
//判断特殊情况
if (len == 1) {
return false;
}
//初始化
Deque<Character> deque = new LinkedList<>();
char[] chs = s.toCharArray();
//函数主体
for (Character ch : chs) {
//堆栈不为空的情况下,栈顶遇到匹配的字符的时候才会弹出,否则一直压栈
if (!deque.isEmpty() && ((deque.peekFirst() == '(' && ch == ')') || (deque.peekFirst() == '{' && ch == '}') || (deque.peekFirst() == '[' && ch == ']'))) {
deque.pollFirst();
} else {
deque.offerFirst(ch);
}
}
deque.offerFirst(ch);
}
}
//返回结果
return deque.isEmpty();
}
}
时间复杂度:O(n)
空间复杂度:O(n)
在较长字符串的情况下可以使用哈希表来提前返回:
其实当栈顶字符和当前字符不匹配的时候就可以判定为false了,没必要继续压栈判断了
class Solution {
public boolean isValid(String s) {
int len = s.length();
//改进1:只要字符数为奇数,肯定不能完全闭合
if ((len & 1) == 1) {
return false;
}
//map记录字符对
Map<Character, Character> map = new HashMap<>() {{
put(')', '(');
put('}', '{');
put(']', '[');
}};
//初始化
char[] chs = s.toCharArray();
Deque<Character> stack = new LinkedList<>();
//函数主体
for (Character ch : chs) {
//如果此时的字符是map的key,就代表需要判断是否弹出,否则压栈等待下一次判断
if (map.containsKey(ch)) {
//改进2:提前返回
//一旦栈顶字符跟value不匹配意味着后面就不可能闭合了,或者右字符要添加到空栈中也无法闭合,所以直接返回false,提前返回,后面没必要判断了
if (stack.isEmpty() || stack.peekFirst() != map.get(ch)) {
return false;
}
stack.pollFirst();
} else {
stack.offerFirst(ch);
}
}
return stack.isEmpty();
}
}
时间复杂度:O(n)
空间复杂度:O(n)
(四) 回溯
解决一个回溯问题,实际上就是一个决策树的遍历过程,是一种穷举算法。
你只需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
回溯算法的框架:
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
46.全排列
class Solution {
//返回结果,全局域
private List<List<Integer>> result = new LinkedList<>();
public List<List<Integer>> permute(int[] nums) {
//记录路径
LinkedList<Integer> track = new LinkedList<>();
backtrack(nums, track);
return result;
}
public void backtrack(int[] nums, LinkedList<Integer> track) {
//当到达叶子节点时,更新结果列表
if (track.size() == nums.length) {
result.add(new LinkedList(track));
return;
}
//遍历数组中的每一个数
for (int i = 0; i < nums.length; i++) {
//排除已经添加的重复元素
if (track.contains(nums[i])) {
continue;
}
//做选择
track.add(nums[i]);
//递归回溯,进入下一层决策树
backtrack(nums, track);
//撤销选择
track.removeLast();
}
}
}
注意⚠️:
- 类型选择LinkedList方便删除最近一个元素,并且声明的时候,不要new List
(), 直接LinkedList<>()就行。 - result.add(track); 这样写返回的都为空,因为是浅拷贝,刚开始值是赋进去了,但是后面remove了之前add的arraylist地址里的数据,所以为空。
时间复杂度:O(nnn! )
递归函数的时间复杂度 = 递归函数本身的复杂度 * 递归函数被调用的次数(决策树上节点的个数) = n*n * n!
空间复杂度:O(n)
关于去除重复元素的方法还有两种:可将时间复杂度将为O(n*n! )
- 交换元素
- 记录在当前路径上某节点是否被遍历过
51.N皇后
class Solution {
//结果集
private List<List<String>> result = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
//棋盘布局
ArrayList<StringBuilder> board = new ArrayList<>();
//初始化棋盘为空
StringBuilder tmp = new StringBuilder();
for (int i = 0; i < n; i++) {
tmp.append('.');
}
for (int i = 0; i < n; i++) {
board.add(new StringBuilder(tmp));
}
//回溯
backtrack(board, 0);
//返回结果
return result;
}
public void backtrack(ArrayList<StringBuilder> board, int row) {
//获取总行数/列数
int n = board.size();
//当到第n行时转化为string添加到结果集中
if (row == n) {
ArrayList<String> tmp = new ArrayList<String>();
for (int i = 0; i < n; i++) {
tmp.add(board.get(i).toString());
}
result.add(tmp);
return;
}
//遍历每一行的每一列
for (int col = 0; col < n; col++) {
//当前坐标不能放置皇后
if (!isValid(board, row, col)) {
continue;
}
board.get(row).setCharAt(col, 'Q');
backtrack(board, row+1);
board.get(row).setCharAt(col, '.');
}
}
//判断是否可以在目标位置放皇后
boolean isValid(ArrayList<StringBuilder> track, int row, int col){
int n = track.size();
// 检查列是否有皇后冲突
for(int i = 0; i < n; i++){
if(track.get(i).charAt(col) == 'Q')
return false;
}
// 检查右上方是否有皇后冲突
for(int i = row-1, j = col+1;
i >=0 && j <n; i--,j++) {
if(track.get(i).charAt(j) == 'Q')
return false;
}
// 检查左上方是否有皇后冲突
for(int i= row-1, j = col-1;
i >=0 && j >=0; i--,j--) {
if(track.get(i).charAt(j) == 'Q')
return false;
}
return true;
}
}
时间复杂度:O(n*n * n叉树的节点数 )
n叉树的节点数 = n^n,但是还有isvalid进行剪枝,但是肯定是指数级的时间复杂度。
空间复杂度:O(n)