信息安全基础—对称/非对称密码图文详解

---

前言

本文旨在讲述几种经典的加密算法，可以用于信息安全导论or密码学的期末复习，或者是兴趣科普。

一、对称密码

一种加解密使用相同密钥的密码体制。解密算法是加密算法的逆过程。使用代替和置换技术。其安全性依赖于所持有密钥的安全性。
五要素：明文、加密算法、密钥、密文、解密算法

1.1、DES

DES全称Data Encryption Standard（数据加密标准），遗憾的是它已经过时了，不过仍值得我们学习。
它是一种分组加密算法，首先将明文分成若干组，每组的明文大小为64位。密钥长64位(bit），但是每个第8位是奇偶校验位，所以是其余56位参与运算。

流程如上所示：首先将明文进行IP置换，然后进行16轮迭代，最后再进行IP逆置换得到密文。
将初始IP置换后的数据分为等长的两个单元，一个叫L0，一个叫R0。然后每一轮迭代的内容如下：

1. L1=R0，R1=F(L0) …以此类推。意为：每一轮的L直接等于上一轮的R，而这一轮的R等于上一轮的L经过函数F变换得到。接下来介绍这个轮函数F的流程
2. R0（32位）首先进行扩展到48位，扩展方法如下：4×8变成了6×8；
   
3. 扩展后的48位数据与48位密钥进行异或计算
4. 计算后的数据（48位）再进行S盒压缩到32位，压缩方法如下：对于每个6位数据，进行下图计算，得到行列数，再去表中查询得到10进制数，最后转换成一个4位数据。
   
   
5. S盒所得结果再经过P盒置换，这样轮函数就结束了。

然后来说明一下，前文不是提到密钥除去校验位还有（64-8）56位吗。为何在轮函数中，与数据进行异或操作的是48位密钥呢？下图讲述了每一轮密钥的的生成

• 其中置换表PC1是56位的，将64位置换成54位。
• 表PC2是48位的，将54位的置换成48位。从而得到了每一轮的密钥K，都是48位

1.2、2DES与3DES

由于DES密码长度容易被暴力破解，所以3DES算法通过对DES算法进行改进，增加DES的密钥长度来避免类似的攻击，针对每个数据块进行两次或者三次DES加密；因此，2DES、3DES加密算法并非什么新的加密算法，是DES的一个更安全的变形，它以DES为基本模块，通过组合分组方法设计出分组加密算法。安全性有所提高，但速度变慢。、
二重DES：
使用两个密钥K1,K2
（1）用K1进行加密
（2）用K2对（1）结果加密
三重DES：
使用两个密钥K1,K2
（1）用K1进行加密
（2）用K2对（1）结果解密
（3）再用K1对（2）结果加密

1.3、AES

也是一种分组加密算法，明文被划分为128位一组。密钥长度不固定，可以是128、192、256位。
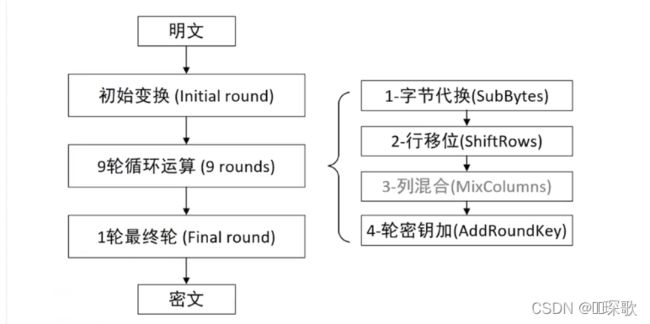
本文将以明文和密钥都是128位来举例讲解。AES加密算法基本流程如下：

• 一个128位，也就是16字节的明文，可以从上到下，从左到右排列成一个4×4的矩阵。 128位密钥也是同理可以表示成4×4的矩阵。

• 初始变换，就是将16字节的明文和16字节的密钥进行异或操作，如下：异或操作是明文的每一列和密文的每一列进行异或，最后也得到一个4×4矩阵。
  

• 9轮循环运算中，每轮都要经过字节代换、行移位、列混合、轮密钥加。最后1轮则不需要经过列混合，其余的也都需要。

接下来讲述每轮循环运算中的关键步骤：

1. 字节变换：对一个4×4的矩阵，进行查表（S盒），比如19就查（x=1,y=19）到为d4
   
   最后就得到了一个新的4×4数据块：
   

2. 行移位：第二的元素都向前移动一位，比如【27\ bf \ b4 \ 41】移位后得到【bf \ b4 \ 41 \ 27】；第三行的元素都向前移动两位；第四行的元素都向前移动三位。

3. 列混合：是将矩阵乘以一个给定的矩阵，这里的乘法是定义在有限域GF(2^8)上的一个乘法。

4. 轮密钥加：将列混合的结果与子密钥进行异或，得到矩阵。那么每一轮的子密钥是如何得到的呢？是通过密钥扩展得到的。具体方法可见最后参考网址。

二、非对称密码

非对称密码又叫公钥密码：这种密码体制使用两个密钥来进行加密和解密，这个两密钥分别是公钥和私钥。公钥和私钥是一对，如果使用公钥对数据进行加密，只有用对应的私钥才能解密，如果用私钥进行加密，只有用相应的公钥才能解密。因为加/解密使用两个不同的密钥，所以这种算法叫做非对称算法。
公钥密码体制的六要素：明文、加密算法、公钥、密钥、解密算法、密文 。

2.1、RSA

RSA公钥加密算法是1977年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起提出的。1987年首次公布，RSA就是他们三人姓氏开头字母拼在一起组成的。RSA是目前最有影响力的公钥加密算法，它能够抵抗到目前为止已知的绝大多数密码攻击，已被ISO推荐为公钥数据加密标准。

RSA算法基于一个十分简单的数论事实：将两个大质（素）数相乘十分容易，但是想要对其乘积进行因式分解却极其困难，我们小学时学过质因数分解6=2*3，但是让你分解一个几百位的数呢？显然不会，对计算机来说都难以做到。

算法步骤如下：

1. 选取两个大素数p和q，（大素数，就是很大很大的素数）
2. n=pq
3. 计算 φ(n)=(p-1)(q-1)，这里的φ是欧拉函数
4. 随便选一个e与φ(n)互质，且1
5. 由公式ed mod φ(n) =1 ，得到d
6. 公钥为（e,n)，私钥为（d,n）

加解密的方法如下：

• 加密：已知明文M，密文C=M^e mod n
• 加密：已知密文C，明文M=C^d mod n

举个栗子：

1. 选取p=3，q=5
2. n=pq=15
3. 计算 φ(n)=(p-1)(q-1)=8
4. 选e=3，因为3和8互质，且1<3<8
5. 3d mod 8 =1 ，得到d=11 （公钥私钥不一样）
6. 公钥为（3,15)，私钥为（11,15）

假如你要发送明文2
根据公钥加密：密文 = 2^3 mod 15 = 8
接收者收到密文8
根据私钥解密：明文 = 8^11 mod 15 = 2

2.2、ECC椭圆曲线

椭圆曲线加密算法比起RSA加密算法在数学层面上读起来更难懂，我将尝试用一种图形化的方法来阐述，而弱化其数学含义，这样可能比较容易理解。
椭圆曲线的方程如下：

椭圆曲线上有两点P、Q，且Q=kP、P称为基点，Q为公钥，k为私钥。
给定k和P计算Q很简单，但给定Q,P计算k确很难
注意：这里的乘法并不是我们常见的那种简单的乘法，而是定义在有限域GF上的一个“乘法”，接下来我会介绍这里的加法和乘法运算

加法：
已知椭圆曲线上的两点A，B。直线AB交椭圆曲线于点C（不相交的情况暂不考虑），点C作y轴平行线交椭圆曲线得到点D。
这时我们定义一个加法：A+B=D

乘法：
想象一下当曲线上两点无限接近时，其实两点连线就是该点切线了。
过椭圆曲线上一点A做切线，交曲线于一点，再做y轴平行线，得到B。
根据加法定义A+A=B 也就是说2A=B。这就叫点的自累，其实就是在做乘法。

那么我们怎么计算3A呢？很简单，重复加法操作

你会发现，这些乘法运算，每次的结果都在跳来跳去找不到规律，这就是椭圆曲线加密的根基。

上图为一随手画的示意图，为了凸显出运算结果的杂乱无章。
在普通的代数运算中5*？=10，小学生也知道另一个乘数为2，但是在椭圆曲线运算中无法倒推，这个逆过程又叫椭圆离散对数问题。

接下讲算法步骤：

1. 选一条椭圆曲线，然后选一点P作为基点
2. 选一个大数k作为私钥
3. 公钥Q=kP

加解密的方法如下：
加密：已知明文M，选择随机数r，密文C是一个点对。C=（rP，M+rQ）
解密：收到密文C=（rP，M+rQ)，
M+rQ-k(rP)=M+rQ-rQ=M
就还原出M了。

关于椭圆曲线更多的数论基础，读者可以自行学习。我在未来会专门写一篇博客来讲述有限域及相关概念。

参考网址

B站【DES加密算法】up主：可厉害的土豆
B站【AES加密算法】up主：可厉害的土豆
Elliptic Curve Diffie Hellman - 椭圆曲线密钥交换