[强化学习实战]深度Q学习-DQN算法原理
深度Q学习
深度Q学习将深度学习和强化学习相结合,是第一个深度强化学习算法。深度Q学习的核心就是用一个人工神经网络 q ( s , a ; w ) , s ∈ S , a ∈ A q(s,a;w),s∈\mathcal{S} ,a∈\mathcal{A} q(s,a;w),s∈S,a∈A 来代替动作价值函数。由于神经网络具有强大的表达能力,能够自动寻找特征,所以采用神经网络有潜力比传统人工特征强大得多。最近基于深度Q网络的深度强化学习算法有了重大的进展,在目前学术界有非常大的影响力。
·经验回放(experience replay):将经验(即历史的状态、动作、奖励等)存储起来,再在存储的经验中按一定的规则采样。
·目标网络(target network):修改网络的更新方式,例如不把刚学习到的网络权重马上用于后续的自益过程。
经验回放
V.Mnih等在2013年发表文章《Playing Atari with deep reinforcement learning》,提出了基于经验回放的深度Q网络,标志着深度Q网络的诞生,也标志着深度强化学习的诞生。
采用批处理的模式能够提供稳定性。经验回放就是一种让经验的概率分布变得稳定的技术,它能提高训练的稳定性。经验回放主要有“存储”和“采样回放”两大关键步骤。
·存储:将轨迹以 ( S t , A t , R t + 1 , S t + 1 ) (S_t,A_t,R_{t+1},S_{t+1}) (St,At,Rt+1,St+1)等形式存储起来;
·采样回放:使用某种规则从存储的 ( S t , A t , R t + 1 , S t + 1 ) (S_t,A_t,R_{t+1},S_{t+1}) (St,At,Rt+1,St+1)中随机取出一条或多条经验。
算法9给出了带经验回放的Q学习最优策略求解算法。
算法9 带经验回放的Q学习最优策略求解
1.(初始化)任意初始化参数 w w w。
2.逐回合执行以下操作。
2.1 (初始化状态动作对)选择状态 S S S。
2.2 如果回合未结束,执行以下操作:
2.2.1 (采样)根据 q ( S , ⋅ ; w ) q(S,·;w) q(S,⋅;w)选择动作A并执行,观测得到奖励R和新状态S’;
2.2.2 (存储)将经验 ( S , A , R , S ′ ) (S,A,R,S') (S,A,R,S′)存入经验库中;
2.2.3 (回放)从经验库中选取经验 ( S i , A i , R i , S i ′ ) (S_i,A_i,R_i,S_i') (Si,Ai,Ri,Si′);
2.2.4 (计算回报的估计值) U i ← R i + γ m a x a q ( S i ′ , a ; w ) Ui←Ri+γmaxaq(S_i',a;w) Ui←Ri+γmaxaq(Si′,a;w);
2.2.5 (更新动作价值函数)更新 w w w以减小 [ U i − q ( S i , A i ; w ) ] 2 ( 如 w ← w + α [ U i − q ( S i , A i ; w ) ] ▽ q ( S i , A i ; w ) ) [U_{i} -q (Si,Ai;w)]^2(如w←w+α[U_i-q(S_i,A_i;w)]▽q(S_i,A_i;w)) [Ui−q(Si,Ai;w)]2(如w←w+α[Ui−q(Si,Ai;w)]▽q(Si,Ai;w))
2.2.6 S ← S ′ S←S' S←S′。
经验回放有以下好处。
·在训练Q网络时,可以消除数据的关联,使得数据更像是独立同分布的(独立同分布是很多有监督学习的证明条件)。这样可以减小参数更新的方差,加快收敛。
·能够重复使用经验,对于数据获取困难的情况尤其有用。从存储的角度,经验回放可以分为集中式回放和分布式回放。
·集中式回放:智能体在一个环境中运行,把经验统一存储在经验池中。
·分布式回放:智能体的多份拷贝(worker)同时在多个环境中运行,并将经验统一存储于经验池中。由于多个智能体拷贝同时生成经验,所以能够在使用更多资源的同时更快地收集经验。
从采样的角度,经验回放可以分为均匀回放和优先回放。
·均匀回放:等概率从经验集中取经验,并且用取得的经验来更新最优价值函数。
·优先回放(Prioritized Experience Replay,PER):为经验池里的每个经验指定一个优先级,在选取经验时更倾向于选择优先级高的经验。
T.Schaul等于2016年发表文章《Prioritized experience replay》,提出了优先回放。优先回放的基本思想是为经验池里的经验指定一个优先级,在选取经验时更倾向于选择优先级高的经验。一般的做法是,如果某个经验(例如经验i)的优先级为 p i p_i pi,那么选取该经验的概率为
![[强化学习实战]深度Q学习-DQN算法原理_第1张图片](http://img.e-com-net.com/image/info8/4909cacebe684e8d8d768d60e1e40414.jpg)
经验值有许多不同的选取方法,最常见的选取方法有成比例优先和基于排序优先。
·成比例优先(proportional priority):第i个经验的优先级为 p i = ( δ i + ε ) α p_i=(δ_i+ε)α pi=(δi+ε)α其中 δ i δ_i δi是时序差分误差, ε ε ε是预先选择的一个小正数, α α α是正参数。
·基于排序优先(rank-based priority):第i个经验的优先级为
![[强化学习实战]深度Q学习-DQN算法原理_第2张图片](http://img.e-com-net.com/image/info8/d38bdc633666436da8e2b2a8040c1c05.jpg)
其中 r a n k i rank_i ranki是第i个经验从大到小排序的排名,排名从1开始。D.Horgan等在2018发表文章《Distributed prioritized experience replay》,将分布式经验回放和优先经验回放相结合,得到分布式优先经验回放(distributed prioritized experience replay)。经验回放也不是完全没有缺点。例如,它也会导致回合更新和多步学习算法无法使用。一般情况下,如果我们将经验回放用于Q学习,就规避了这个缺点。
带目标网络的深度Q学习
对于基于自益的Q学习,其回报的估计和动作价值的估计都和权重 w w w有关。当权重值变化时,回报的估计和动作价值的估计都会变化。在学习的过程中,动作价值试图追逐一个变化的回报,也容易出现不稳定的情况。在半梯度下降中,在更新价值参数 w w w时,不对基于自益得到的回报估计Ut求梯度。其中一种阻止对Ut求梯度的方法就是将价值参数复制一份得到 w w w目标,在计算 U t U_t Ut时用w目标计算。基于这一方法,V.Mnih等在2015年发表了论文《Human-level control through deep reinforcement learning》,提出了目标网络(target network)这一概念。目标网络是在原有的神经网络之外再搭建一份结构完全相同的网络。原先就有的神经网络称为评估网络(evaluation network)。在学习的过程中,使用目标网络来进行自益得到回报的评估值,作为学习的目标。在权重更新的过程中,只更新评估网络的权重,而不更新目标网络的权重。这样,更新权重时针对的目标不会在每次迭代都变化,是一个固定的目标。在完成一定次数的更新后,再将评估网络的权重值赋给目标网络,进而进行下一批更新。这样,目标网络也能得到更新。由于在目标网络没有变化的一段时间内回报的估计是相对固定的,目标网络的引入增加了学习的稳定性。所以,目标网络目前已经成为深度Q学习的主流做法。
算法10给出了带目标网络的深度Q学习算法。算法开始时将评估网络和目标网络初始化为相同的值。为了得到好的训练效果,应当按照神经网络的相关规则仔细初始化神经网络的参数。
算法10 带经验回放和目标网络的深度Q学习最优策略求解
1.(初始化)初始化评估网络 q ( ⋅ , ⋅ ; w ) q(·,·;w) q(⋅,⋅;w)的参数w;目标网络 q ( ⋅ , ⋅ ; w 目 标 ) q(·,·;w_{目标}) q(⋅,⋅;w目标)的参数 w 目 标 ← w w_{目标}←w w目标←w。
2.逐回合执行以下操作。
2.1 (初始化状态动作对)选择状态 S S S。
2.2 如果回合未结束,执行以下操作:
2.2.1 (采样)根据 q ( S , ⋅ ; w ) q(S,·;w) q(S,⋅;w)选择动作A并执行,观测得到奖励R和新状态S’;
2.2.2 (经验存储)将经验 ( S , A , R , S ′ ) (S,A,R,S') (S,A,R,S′)存入经验库中;
2.2.3 (经验回放)从经验库中选取一批经验 ( S i , A i , R i , S i ′ ) ( i ∈ B ) (S_i,A_i,R_i,S_i')(i∈ \mathcal{B}) (Si,Ai,Ri,Si′)(i∈B);
2.2.4 (计算回报的估计值)
2.2.5 (更新动作价值函数)更新以减小
2.2.6 S ← S ′ S←S' S←S′;
2.2.7 (更新目标网络)在一定条件下(例如访问本步若干次)更新目标网络的权重 w 目 标 ← w w_{目标}←w w目标←w。
在更新目标网络时,可以简单地把评估网络的参数直接赋值给目标网络(即 w 目 标 ← w w_{目标}←w w目标←w),也可以引入一个学习率α目标把旧的目标网络参数和新的评估网络参数直接做加权平均后的值赋值给目标网络(即 w 目 标 ← ( 1 − α 目 标 ) w 目 标 + α 目 标 w w_{目标}←(1-α_{目标})w_{目标}+α_{目标}w w目标←(1−α目标)w目标+α目标w)。事实上,直接赋值的版本是带学习率版本在 α 目 标 = 1 α_{目标}=1 α目标=1时的特例。对于分布式学习的情形,有很多独立的拷贝(worker)同时会修改目标网络,则就更常用学习率 α 目 标 ∈ ( 0 , 1 ) α_{目标}∈(0,1) α目标∈(0,1)。
双重深度Q网络
Q学习会带来最大化偏差,而双重Q学习却可以消除最大化偏差。基于查找表的双重Q学习引入了两个动作价值的估计 q ( 0 ) 和 q ( 1 ) q^{(0)}和q^{(1)} q(0)和q(1),每次更新动作价值时用其中的一个网络确定动作,用确定的动作和另外一个网络来估计回报。
对于深度Q学习也有同样的结论。Deepmind于2015年发表论文《Deep reinforcement learning with double Q-learning》,将双重Q学习用于深度Q网络,得到了双重深度Q网络(Double Deep Q Network,Double DQN)。考虑到深度Q网络已经有了评估网络和目标网络两个网络,所以双重深度Q学习在估计回报时只需要用评估网络确定动作,用目标网络确定回报的估计即可。所以,只需要将算法10中的

更换为

就得到了带经验回放的双重深度Q网络算法。
对偶深度Q网络
Z.Wang等在2015年发表论文《Dueling network architectures for deep reinforcement learning》,提出了一种神经网络的结构——对偶网络(duel network)。对偶网络理论利用动作价值函数和状态价值函数之差定义了一个新的函数——优势函数(advantage function):
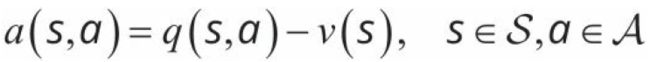
对偶Q网络仍然用 q ( w ) q(w) q(w)来估计动作价值,只不过这时候 q ( w ) q(w) q(w)是状态价值估计 v ( s ; w ) v(s;w) v(s;w)和优势函数估计 a ( s , a ; w ) a(s,a;w) a(s,a;w)的叠加,即 q ( s , a ; w ) = v ( s ; w ) + a ( s , a ; w ) q(s,a;w)=v(s;w)+a(s,a;w) q(s,a;w)=v(s;w)+a(s,a;w)。
其中 v ( w v(w v(w)和 a ( w ) a(w) a(w)可能都只用到了 w w w中的部分参数。在训练的过程中, v ( w ) v(w) v(w)和 a ( w ) a(w) a(w)是共同训练的,训练过程和单独训练普通深度Q网络并无不同之处。
不过,同一个q(w)事实上存在着无穷多种分解为v(w)和a(w)的方式。如果某个 q ( s , a ; w ) q(s,a;w) q(s,a;w)可以分解为某个 v ( s ; w ) 和 a ( s , a ; w ) v(s;w)和a(s,a;w) v(s;w)和a(s,a;w),那么它也能分解为 v ( s ; w ) + c ( s ) v(s;w)+c(s) v(s;w)+c(s)和 a ( s , a ; w ) − c ( s ) a(s,a;w)-c(s) a(s,a;w)−c(s),其中 c ( s ) c(s) c(s)是任意一个只和状态 s s s有关的函数。为了不给训练带来不必要的麻烦,往往可以通过增加一个由优势函数导出的量,使得等效的优势函数满足固定的特征,使得分解唯一。常见的方法有以下两种:
·考虑优势函数的最大值,令

使得等效优势函数 a 等 效 ( s , a ; w ) = a ( s , a ; w ) − max a ( s , a ; w ) a_{等效}(s,a;w) = a(s,a;w)-\max{a(s,a;w)} a等效(s,a;w)=a(s,a;w)−maxa(s,a;w)满足

·考虑优势函数的平均值,令

使得等效优势函数 a 等 效 ( s , a ; w ) = a ( s , a ; w ) − 1 ∣ A ∣ ∑ a ( s , a ; w ) a_{等效}(s,a;w)=a(s,a;w)-\dfrac{1}{|{A}|}\sum{a(s,a;w)} a等效(s,a;w)=a(s,a;w)−∣A∣1∑a(s,a;w)满足
![[强化学习实战]深度Q学习-DQN算法原理_第3张图片](http://img.e-com-net.com/image/info8/1868986129a24473b3e2a550befc6fb8.jpg)

