Python-并查集详解与实现

目录

简介

初始化（帮派林立）

查询与合并（帮派争斗）

路径压缩（大江湖帮派争斗）

按高度合并

按节点总数合并

结果

全部代码

相关题目

---

简介

数据结构：树的双亲表示法，即一个列表fa，fa[i] = j，i的父节点为j

采用经典的帮派打架【找不到谁是第一作者了，在此表示感谢】来讲解：帮派->树、老大->根节点。

初始化（帮派林立）

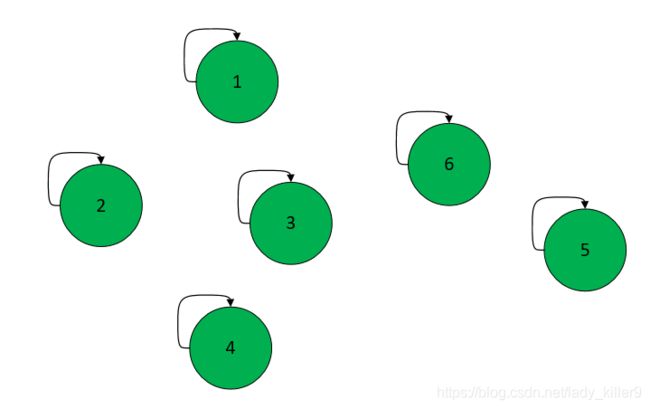
刚开始，江湖上有很多帮派，帮派就一个人，“张三派”、“李四派”等，谁也不服谁。

初始化，绿色代表根节点

 

    def __init__(self, n, hi=False):
        self.fa = [i for i in range(n)]

每个帮派只有一个人，即自己是自己的老大==>自己是自己的根节点。

查询与合并（帮派争斗）

江湖开始了不断的厮杀。。。

合并

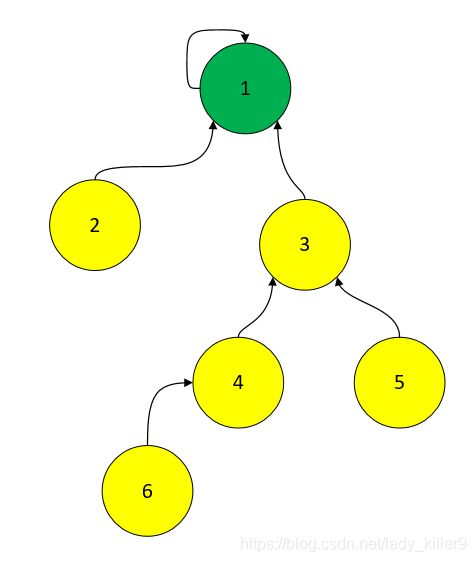
2->1：1和2打了一架，2输了，1说：“你输了，我以后就是你老大了”

5->3：5和3打了一架，5输了，3说：“你输了，我以后就是你老大了”

6->4：自行补充

4->3：自行补充

3->1：2和5要打架，他俩寻思，我们都有老大了，咱俩不管谁赢了，老大不服气，还是要打架，干脆让他俩打吧，谁老大输了，直接老大带着整个帮派拜另一个帮派的老大为老大，于是，2找了老大1，5找了老大3，1和3打了一架，3输了，于是3带着5、4、6都投奔到了1的门下。

    def find(self, val):
        """
        normal find, get father of val
        :param val: a node's value
        :return: root of val
        """
        if self.fa[val] == val:
            return val
        else:
            return self.find(self.fa[val])

找到老大==>找到根节点

参数

val：节点的值

    def union(self, val1, val2):
        """
        normal union, make val1's father equal val2's father
        :param val1: a node's value
        :param val2: another node's value
        :return: None
        """
        self.fa[self.find(val1)] = self.fa[self.find(val2)]
        return None

输的一派的老大拜赢得帮派的老大为老大==>【val1是输的】val1所在树的根节点的父节点为val2所在树的根节点

合并树/集合

参数

val1:需要被合并的

val2:合并其他树/集合的

路径压缩（大江湖帮派争斗）

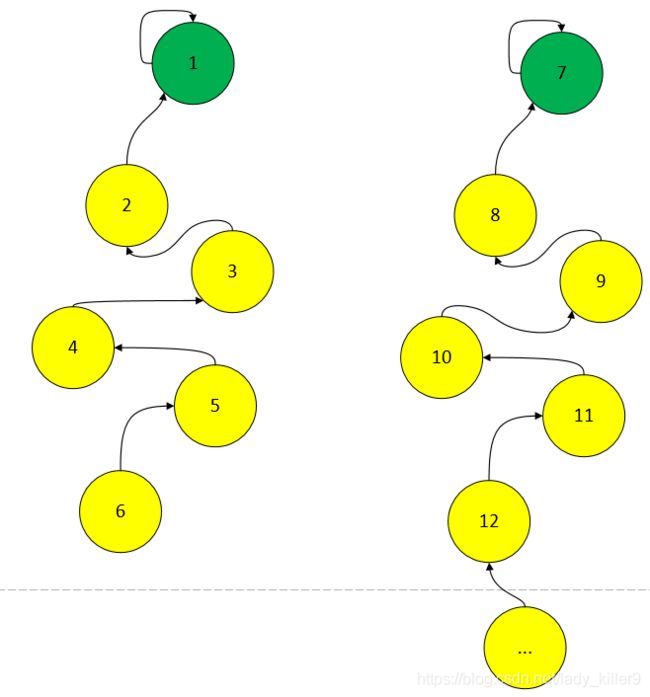
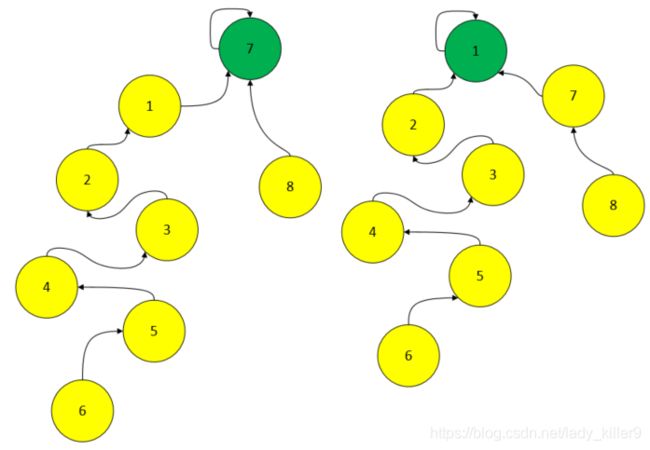
假如上面的江湖之中，6先和5打架，之后是5和4，每次都是后者赢，依次类推，形成上图（左）。又有另一江湖，形成了上图（右），此时，6和另一帮派的...想要打架，...可能是10000甚至更多，等它找到他的老大时就太晚了。由于我们只关心谁是帮派的老大，所以可以在每次查询老大时，把沿途的每个节点的父节点都设为根节点

比喻结束！！！

按高度合并

实际上，没有输赢，我们才是“幕后黑手”。前面的合并是我们随意选择的，并没有根据帮派（树）的特点来进行合并。

为了让江湖厮杀更快一点，我们每次都让低的树合并到高的一方，即上图（右），而不是上图（左）。这样让合并后的树相对低一点。

    def union_compress(self, val1, val2):
        """
        union according to height of tree
        :param val1:  a node's value
        :param val2:  another node's value
        :return: None
        """
        x, y = self.find(val1), self.find(val2)
        if self.hi[x] <= self.hi[y]:
            self.fa[x] = y
        else:
            self.fa[y] = x
        if self.hi[x] == self.hi[y] and x != y:
            self.hi[y] += 1
        return None

根据高度合并，不像前面一定是第一个节点所在树合并到第二个上

参数

• val1：节点的值
• val2：另一节点的值

    def find_compress(self, val):
        """
        find with path compress
        :param val:  a node's value
        :return: father of val, val 's father equal val's root
        """
        if self.fa[val] == val:
            return val
        else:
            self.fa[val] = self.find(self.fa[val])
            return self.fa[val]

查找时路径压缩，找根节点时，设置自己的父节点为根节点

val：节点的值

按节点总数合并

仅提一下，不画图了。按秩合并的一种，秩的选取为树的节点总数，稍微改一下就好了。还有其他的路径压缩方法，不一一列举了。

结果

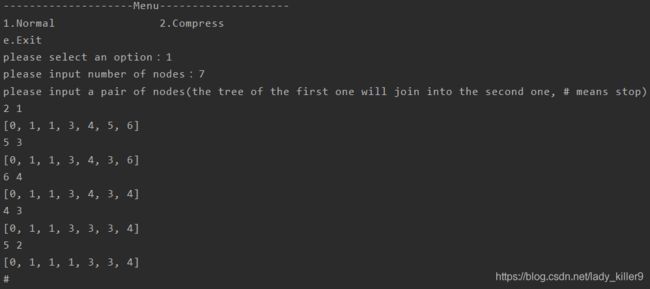
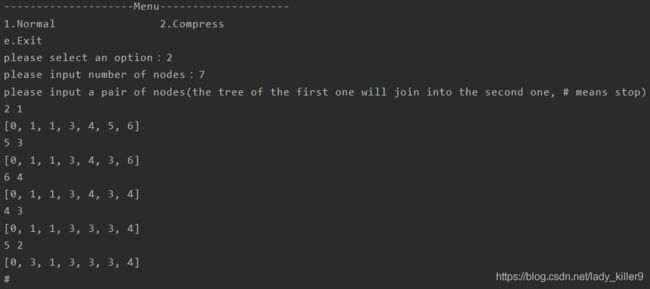
输入数据

7
2 1
5 3
6 4
4 3
5 2

无路径压缩

 

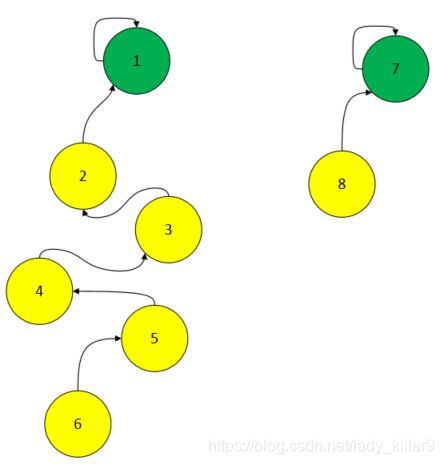
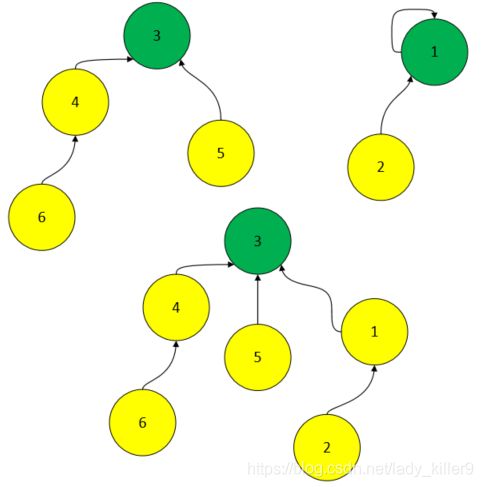
 有路径压缩时，对应的最后一步合并如下。

全部代码

"""
--coding:utf-8--
@File: DisjointSet.py.py
@Author:frank yu
@DateTime: 2021.01.17 19:50
@Contact: [email protected]
@Description:
"""


class DisjointSet:
    def __init__(self, n, hi=False):
        self.fa = [i for i in range(n)]
        self.hi = []
        if hi:
            self.hi = [1 for _ in range(n)]

    def union(self, val1, val2):
        """
        normal union, make val1's father equal val2's father
        :param val1: value of node which need to change root
        :param val2: another node's value
        :return: None
        """
        self.fa[self.find(val1)] = self.find(val2)
        return None

    def find(self, val):
        """
        normal find, get father of val
        :param val: a node's value
        :return: root of val
        """
        if self.fa[val] == val:
            return val
        else:
            return self.find(self.fa[val])

    def union_compress(self, val1, val2):
        """
        union according to height of tree
        :param val1:  a node's value
        :param val2:  another node's value
        :return: None
        """
        x, y = self.find(val1), self.find(val2)
        if self.hi[x] <= self.hi[y]:
            self.fa[x] = y
        else:
            self.fa[y] = x
        if self.hi[x] == self.hi[y] and x != y:
            self.hi[y] += 1
        return None

    def find_compress(self, val):
        """
        find with path compress
        :param val:  a node's value
        :return: father of val, val 's father equal val's root
        """
        if self.fa[val] == val:
            return val
        else:
            self.fa[val] = self.find(self.fa[val])
            return self.fa[val]

    def show(self):
        print(self.fa)


def menu():
    print('--------------------Menu--------------------')
    print('1.Normal                2.Compress')
    print('e.Exit')


if __name__ == '__main__':
    while True:
        menu()
        choice = input('please select an option：')
        if choice == 'e':
            break
        n = input('please input number of nodes：')
        if choice == '1':
            d = DisjointSet(int(n))
            print('please input a pair of nodes(the tree of the first one will join into the second one, # means stop)')
            while True:
                seq = input()
                if seq == '#':
                    break
                else:
                    i, j = list(map(int, seq.split()))
                    d.union(i, j)
                    d.show()
        else:
            d = DisjointSet(int(n), True)
            print('please input a pair of nodes(the tree of the first one will join into the second one, # means stop)')
            while True:
                seq = input()
                if seq == '#':
                    break
                else:
                    i, j = list(map(int, seq.split()))
                    d.union_compress(i, j)
                    d.show()

相关题目

Leetcode 547 省份数量

Leetcode 200 岛屿数量

除法求值

交换字符串中的元素

冗余连接

移除最多同行列的石头

打砖块

账户合并

连接所有点的最小费用

1319. 连通网络的操作次数

由斜杠划分区域

1579. 保证图可完全遍历

1631. 最小体力消耗路径

839. 相似字符串组