从零构建深度学习推理框架-4 框架中的算子注册机制

今天要讲的这一注册机制用到了设计模式中的工厂模式和单例模式，所以这节课也是对两大设计模式的一个合理应用和实践。KuiperInfer的注册表是一个map数据结构，维护了一组键值对，key是对应的OpType，用来查找对应的value，value是用于创建该层的对应方法(Creator)。我们可以看一下KuiperInfer中的Layer注册表实现：

 typedef std::map CreateRegistry;

OpType就是头文件中对应的索引：

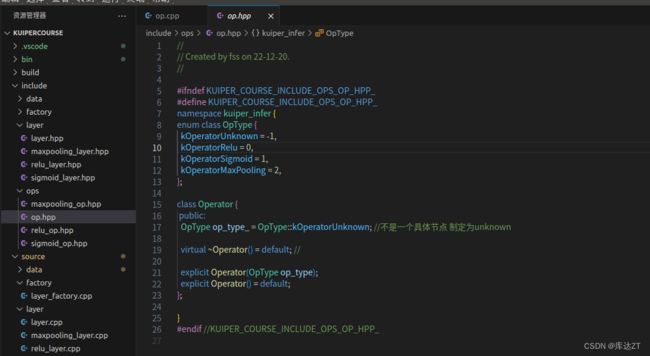创建该层的对应方法相当于一个工厂(Creator)，Creator如下的代码所示，是一个函数指针类型，我们将存放参数的Oprator类传入到该方法中，然后该方法根据Operator内的参数返回具体的Layer.

typedef std::shared_ptr (*Creator)(const std::shared_ptr &op);

代表的是返回值为std::shared_ptr 然后参数为const std::shared_ptr &op的一类函数

只要返回值和参数的类型\个数都满足 creator就可以指向对应的函数

对应函数就是创建层layer的一个具体方法

所以目前就是这个样子：

ReluLayer定义完成--->LayerRegistererWrapper ---> RegisterCreator

接下来我们再看这个registor注册方法：

void LayerRegisterer::RegisterCreator(OpType op_type, const Creator &creator) {
  CHECK(creator != nullptr) << "Layer creator is empty";
  CreateRegistry ®istry = Registry(); //实现单例的关键
  // 根据operator type
  CHECK_EQ(registry.count(op_type), 0) << "Layer type: " << int(op_type) << " has already registered!";
 //  ReluLayer::CreateInstance 没有被注册过,就塞入到注册表当中
  registry.insert({op_type, creator});
}

先来补充一下单例模式：

单例设计编程模式

全局当中有且只有一个变量

任意次和任意一方去调用都会得到这个唯一的变量

这里的唯一变量是全局的注册表 存的时候是这个,取得时候也需要是这个

这里的Registry也写上了，就是实现单例的关键：

LayerRegisterer::CreateRegistry &LayerRegisterer::Registry() {

  // C++程序员高频面试点
  static  CreateRegistry *kRegistry = new CreateRegistry();
  // 没有static 那就是调用一次初始化一次
  // 不构成单例
  CHECK(kRegistry != nullptr) << "Global layer register init failed!";
  return *kRegistry; // 返回了这个注册表
}

static CreateRegistry *kRegistry = new CreateRegistry();

这个其实只会被初始化一次

简单来说第一次,调用的时候 new CreateRegistry 存放到一个kRegistry (static)

后续调用的时候,只会返回kRegistry (static)

这是一种C++的特性。

如果没有static，那就是调用一次就初始化一次，就自然构不成单例模式。

layer_factory.cpp:

namespace kuiper_infer {
// OpType::kOperatorRelu 就是刚才还说的OpType
// ReluLayer::CreateInstance就是一个函数指针,用来初始化层的方法

// 单例设计编程模式
// 全局当中有且只有一个变量
// 任意次和任意一方去调用都会得到这个唯一的变量
// 这里的唯一变量是全局的注册表 存的时候是这个,取得时候也需要是这个
// typedef std::map CreateRegistry
// 全局当中有且只有一个 CreateRegistry  的实例
// 什么方法来控制这个变量唯一呢
void LayerRegisterer::RegisterCreator(OpType op_type, const Creator &creator) {
  CHECK(creator != nullptr) << "Layer creator is empty";
  CreateRegistry ®istry = Registry(); //实现单例的关键
  // 根据operator type
  CHECK_EQ(registry.count(op_type), 0) << "Layer type: " << int(op_type) << " has already registered!";
 //  ReluLayer::CreateInstance 没有被注册过,就塞入到注册表当中
  registry.insert({op_type, creator});
}

  CreateRegistry ®istry = Registry(); //实现单例的关键

这个就是上面的Registry，之后作检查，如果已经有过的话，那count之后就该报错啦。

 CHECK_EQ(registry.count(op_type), 0) << "Layer type: " << int(op_type) << " has already registered!";

没有注册机制的create

然后我们来看一下没有注册机制前的createrelu是怎么做到的：

TEST(test_layer, forward_relu1) {
  using namespace kuiper_infer;
  float thresh = 0.f;
  // 初始化一个relu operator 并设置属性
  std::shared_ptr relu_op = std::make_shared(thresh);

  // 有三个值的一个tensor
  std::shared_ptr> input = std::make_shared>(1, 1, 3);
  input->index(0) = -1.f; //output对应的应该是0
  input->index(1) = -2.f; //output对应的应该是0
  input->index(2) = 3.f; //output对应的应该是3
  // 主要第一个算子，经典又简单，我们这里开始！

  std::vector>> inputs; //作为一个批次去处理

  std::vector>> outputs; //放结果
  inputs.push_back(input);
  ReluLayer layer(relu_op);
  // 因为是4.1 所以没有作业 4.2才有
// 一个批次是1
  layer.Forwards(inputs, outputs);
  ASSERT_EQ(outputs.size(), 1);
//记得切换分支!!!!!
  for (int i = 0; i < outputs.size(); ++i) {
    ASSERT_EQ(outputs.at(i)->index(0), 0.f);
    ASSERT_EQ(outputs.at(i)->index(1), 0.f);
    ASSERT_EQ(outputs.at(i)->index(2), 3.f);
  }
}

有了注册机制后的createrelu：

// 有了注册机制后的框架是如何init layer
TEST(test_layer, forward_relu2) {
  using namespace kuiper_infer;
  float thresh = 0.f;
  std::shared_ptr relu_op = std::make_shared(thresh);
  std::shared_ptr relu_layer = LayerRegisterer::CreateLayer(relu_op);

  std::shared_ptr> input = std::make_shared>(1, 1, 3);
  input->index(0) = -1.f;
  input->index(1) = -2.f;
  input->index(2) = 3.f;
  std::vector>> inputs;
  std::vector>> outputs;
  inputs.push_back(input);
  relu_layer->Forwards(inputs, outputs);
  ASSERT_EQ(outputs.size(), 1);
  for (int i = 0; i < outputs.size(); ++i) {
    ASSERT_EQ(outputs.at(i)->index(0), 0.f);
    ASSERT_EQ(outputs.at(i)->index(1), 0.f);
    ASSERT_EQ(outputs.at(i)->index(2), 3.f);
  }
}

我们可以看到std::shared_ptr relu_op = std::make_shared(thresh), 初始化了一个ReluOperator, 其中的参数为thresh=0.f.

因为我们已经在ReluLayer的实现中完成了注册，{kOperatorRelu:ReluLayer::CreateInstance} , 所以现在可以使用 LayerRegisterer::CreateLayer(relu_op) 得到我们ReluLayer中的实例化工厂方法，我们再来看看CreateLayer的实现：

std::shared_ptr LayerRegisterer::CreateLayer(const std::shared_ptr &op) {
  CreateRegistry ®istry = Registry();
  const OpType op_type = op->op_type_;

  LOG_IF(FATAL, registry.count(op_type) <= 0) << "Can not find the layer type: " << int(op_type);
  const auto &creator = registry.find(op_type)->second;

  LOG_IF(FATAL, !creator) << "Layer creator is empty!";
  std::shared_ptr layer = creator(op);
  LOG_IF(FATAL, !layer) << "Layer init failed!";
  return layer;
}

可以看到传入的参数为op, 我们首先取得op中的op_type, 此处的op_type为kOperatorRelu, 根据registry.find(op_type), 就得到了层的初始化方法creator, 随后使用传入的op去初始化layer并返回实例。值得注意的是此处也调用了CreateRegistry ®istry =Registry() 返回了我们所说的全局有且唯一的Layer注册表。

此处的creator(op)就相当于调用了ReluLayer::CreateInstance.（因为：

LayerRegistererWrapper kReluLayer(OpType::kOperatorRelu, ReluLayer::CreateInstance);

class LayerRegistererWrapper {
 public:
  LayerRegistererWrapper(OpType op_type, const LayerRegisterer::Creator &creator) {
    // 定义之后调用的
    // RegisterCreator
    LayerRegisterer::RegisterCreator(op_type, creator);
  }
};

）

这样子可能看上去和上面差别不大，但是在实际应用上会便捷很多：

ops:[] = {conv 1 , conv 2 ,conv 3 ,relu ,sigmoid ,linear , conv 3};
layers = [];
for op in ops : 
    layers.append(LayerRegisterer::CreateLayer(op))
    //初始化完毕

因为如果没有这个机制的话，那么语言多少层，他就要写多少层。

创建sigmoid算子：

void SigmoidLayer::Forwards(const std::vector>> &inputs,
                            std::vector>> &outputs) {
  CHECK(this->op_ != nullptr);
  CHECK(this->op_->op_type_ == OpType::kOperatorSigmoid);
  CHECK(!inputs.empty());

  const uint32_t batch_size = inputs.size();
  for (uint32_t i = 0; i < batch_size; ++i) {
    const std::shared_ptr> &input_data = inputs.at(i);
    std::shared_ptr> output_data = input_data->Clone();
    //补充,y=1/(1+e^{-x})
    output_data->data().transform([&](float value) {
    return(1/(1+exp(-1*value))); 
    });

    outputs.push_back(output_data);
  }
}

cube的transform函数就是对于这个cube中的每一个元素进行lambda表达式中的运算

在这里预先将input_data进行了复制i，所以可以对于output中的数值进行直接的运算。