动态规划进阶
文章目录
- 状压dp
-
- 小国王
- 玉米田
- 炮兵阵地
- 树形DP
-
- 没有上司的舞会(树形DP)
- 数位DP
-
- 度的数量
- 数字游戏
- Windy数
个人学习笔记!!!
状压dp
状压DP总结:
(1)用二进制表示状态
(2)用位运算筛选出合法状态
(3)用位运算判断状态转移的条件
(4)计算时每个类累加上一行兼容类
一般状压DP给定的数据范围都比较小
小国王
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
public class Main{
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int n = 0, k = 0; //棋盘行数 国王个数
static int cnt = 0; //同一行的合法状态个数
static int[] s = new int[1 << 12]; //同一行的合法状态集
static int[] num = new int[1 << 12]; //每个合法状态包含的国王数
static long[][][] dp = new long[12][144][1 << 12]; //前i行放了j个国王,第i行第a个状态时的方案数
public static void main(String[] args) throws IOException {
String[] nk = br.readLine().split(" ");
n = Integer.parseInt(nk[0]);
k = Integer.parseInt(nk[1]);
//预处理
for(int i = 0; i < (1 << n); i++) {
if((i & i >> 1) == 0) { //不存在相邻的1
s[cnt++] = i; //保存此合法状态
for(int j = 0; j < n; j++) {
num[i] += (i>>j&1); //统计每个合法状态包含1(国王)的个数
}
}
}
// System.out.println(cnt);
// for(int i = 0; i < cnt; i++) {
// System.out.println(Integer.toBinaryString(s[i]) + " " +num[s[i]]);
// }
//DP
dp[0][0][0] = 1; //不放国王也是一种状态
for(int i = 1; i <= n + 1; i++) {//枚举行
for(int j = 0; j <= k; j++) { //枚举国王数
//枚举国王数
for(int a = 0; a < cnt; a++) { //枚举第i行合法状态
for(int b = 0; b < cnt; b++) {
int c = num[s[a]]; //第i行第a个状态的国王数
//可以继续放国王,不存在同列的1,不存在斜对角的1
if((j >= c) && ((s[b] & s[a]) == 0) && ((s[b] & (s[a] << 1)) == 0) && ((s[b]&(s[a]>>1)) == 0)) {
dp[i][j][a] += dp[i-1][j-c][b];
}
}
}
}
}
System.out.println(dp[n+1][k][0]);
}
}
玉米田
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
public class Main{
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int mod = (int) 1e9;
static int n = 0, m = 0; //
static int[][] a = new int[15][15];
static int[] g = new int[15]; //各行土地的状态值
static int cnt = 0; //同一行的合法状态个数
static int[] s = new int[1 << 14]; //同一行的合法状态集
static long[][] dp = new long[15][1 << 15]; //种植了前i行,第i行第a个状态时的方案数
public static void main(String[] args) throws IOException {
String[] nm = br.readLine().split(" ");
n = Integer.parseInt(nm[0]);
m = Integer.parseInt(nm[1]);
//预处理
for(int i = 1;i <= n; i++) {
String[] aa = br.readLine().split(" ");
for(int j = 1; j <= m; j++) {
a[i][j] = Integer.parseInt(aa[j - 1]);
}
}
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
int x = a[i][j];
g[i] = (g[i] << 1) + x;
}
// System.out.println(g[i]);
}
for(int i = 0; i < (1 << m); i++) {
if((i&i >> 1)==0) {
s[cnt++] = i;//保存一行的合法状态
}
}
dp[0][0] = 1;
for(int i = 1; i <= n + 1; i++) {
for(int a = 0; a < cnt; a++) { //第i行
for(int b = 0; b < cnt; b++) { //第i-1行状态
//a种在可以种的地方,a b没有相邻的1
if((s[a] & g[i]) == s[a] && (s[a] & s[b]) == 0) {
dp[i][a] = (dp[i][a] + dp[i-1][b])%mod;
}
}
}
}
//等价于只在1~n行种植
System.out.println(dp[n+1][0]);
}
}
炮兵阵地
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
public class Main{
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int mod = (int) 1e9;
static int n = 0, m = 0; //
static int[] g = new int[110]; //地图各行的数值(1是平原 0是山地)
static int cnt = 0; //同一行的合法状态个数
static int[] s = new int[1 << 15]; //同一行的合法状态集
static int[] num = new int[1<<15]; //计算合法状态包含1的个数
static int[][][] dp = new int[110][1<<11][1<<11]; //种植了前i行,第i行第a个状态时的方案数
static int[][] a = new int[110][11];
public static void main(String[] args) throws IOException {
String[] nm = br.readLine().split(" ");
n = Integer.parseInt(nm[0]);
m = Integer.parseInt(nm[1]);
for(int i =1 ; i <= n; i++) {
String str = br.readLine();
for(int j = 1; j <= m; j++) {
char ch = str.charAt(j - 1);
if(ch == 'P') {
a[i][j] = 1;
}else {
a[i][j] = 0;
}
// System.out.print(a[i][j]);
}
}
//处理地图(存成十进制形式:1:代表平原 0:代表山地)
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
// System.out.print(a[i][j]);
if(a[i][j] == 1) {
g[i] += (1 << (m - j));
}
}
// System.out.println(g[i]);
}
//预处理
for(int i = 0; i < (1 << m); i++) { //枚举一行的所有状态
if((i&i>>1) == 0 && (i&i>>2) == 0) { //11和101不合法
s[cnt++] = i;
for(int j = 0; j < m; j++) {
num[i] += (i>>j&1);
}
}
}
//DP
for(int i = 1; i <= n + 2; i++) {
for(int a = 0; a < cnt; a++) {
for(int b = 0; b < cnt; b++) {
for(int c = 0; c < cnt; c++) {
if(((s[a] & s[b]) == 0) && ((s[b] & s[c]) == 0) &&((s[a] & s[c]) == 0) &&
((g[i] & s[a]) == s[a]) && (g[i-1]&s[b])== s[b]) {
dp[i][a][b] = Math.max(dp[i][a][b],dp[(i-1)][b][c]+num[s[a]]);
}
}
}
}
}
int ans = 0;
// System.out.println(dp[n+2][0][0]);
for(int a = 0; a < cnt; a++) {
for(int b = 0; b < cnt; b++) {
ans = Math.max(ans,dp[n][a][b]);
}
}
System.out.println(ans);
}
}
上述代码会MLE,但是可以看出来我们每次指挥用到i-1的状态,所以可以用二进制滚动优化
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
public class Main{
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int mod = (int) 1e9;
static int n = 0, m = 0; //
static int[] g = new int[110]; //地图各行的数值(1是平原 0是山地)
static int cnt = 0; //同一行的合法状态个数
static int[] s = new int[1 << 15]; //同一行的合法状态集
static int[] num = new int[1<<15]; //计算合法状态包含1的个数
static int[][][] dp = new int[2][1<<11][1<<11]; //种植了前i行,第i行第a个状态时的方案数
static int[][] a = new int[110][11];
public static void main(String[] args) throws IOException {
String[] nm = br.readLine().split(" ");
n = Integer.parseInt(nm[0]);
m = Integer.parseInt(nm[1]);
for(int i =1 ; i <= n; i++) {
String str = br.readLine();
for(int j = 1; j <= m; j++) {
char ch = str.charAt(j - 1);
if(ch == 'P') {
a[i][j] = 1;
}else {
a[i][j] = 0;
}
// System.out.print(a[i][j]);
}
}
//处理地图(存成十进制形式:1:代表平原 0:代表山地)
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
// System.out.print(a[i][j]);
if(a[i][j] == 1) {
g[i] += (1 << (m - j));
}
}
// System.out.println(g[i]);
}
//预处理
for(int i = 0; i < (1 << m); i++) { //枚举一行的所有状态
if((i&i>>1) == 0 && (i&i>>2) == 0) { //11和101不合法
s[cnt++] = i;
for(int j = 0; j < m; j++) {
num[i] += (i>>j&1);
}
}
}
//DP
for(int i = 1; i <= n + 2; i++) {
for(int a = 0; a < cnt; a++) {
for(int b = 0; b < cnt; b++) {
for(int c = 0; c < cnt; c++) {
if(((s[a] & s[b]) == 0) && ((s[b] & s[c]) == 0) &&((s[a] & s[c]) == 0) &&
((g[i] & s[a]) == s[a]) && (g[i-1]&s[b])== s[b]) {
dp[i%2][a][b] = Math.max(dp[i%2][a][b],dp[(i-1)%2][b][c]+num[s[a]]);
}
}
}
}
}
int ans = 0;
// System.out.println(dp[n+2][0][0]);
for(int a = 0; a < cnt; a++) {
for(int b = 0; b < cnt; b++) {
ans = Math.max(ans,dp[n%2][a][b]);
}
}
System.out.println(ans);
}
}
完美AC!
树形DP
没有上司的舞会(树形DP)
数位DP
度的数量
看到肯定第一眼就能看出来暴力求解方法,直接枚举区间内的所有数,检查是否满足条件:
转为b进制数,除了k个1外,其他均是0。
显然时间复杂度太大,肯定会TLE
public static void main(String[] args) throws Exception{
String[] xy = br.readLine().split(" ");
x = Integer.parseInt(xy[0]);
y = Integer.parseInt(xy[1]);
k = Integer.parseInt(br.readLine());
b = Integer.parseInt(br.readLine());
long ans = 0;
for(int i = x; i <= y; i++) {
if(check(i)) {
if(iszero(i)) {
ans += 1;
}
}
}
System.out.println(ans);
}
private static boolean iszero(int x) {
String s = Integer.toString(x, b);
for(int i = 0; i < s.length(); i++) {
if(s.charAt(i) != '1' && s.charAt(i) != '0') {
return false;
}
}
return true;
}
private static boolean check(int x) {
String s = Integer.toString(x, b);
// System.out.println(s);
int count = 0;
for(int i = 0; i < s.length(); i++) {
if(count > k) {
return false;
}
if(s.charAt(i) == '1') {
count++;
}
}
if(count == k) {
return true;
}else {
return false;
}
}
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int N = 34; //数据范围是2的31
static int n = 0,q = 0;
static int[] a = new int[N];
static int[][] f = new int[N][N]; //f[i][j]表示在i个位置上,放置j个1的组合数
static int x = 0, y = 0, k = 0, b = 0;
public static void main(String[] args) throws Exception{
init();
String[] xy = br.readLine().split(" ");
x = Integer.parseInt(xy[0]);
y = Integer.parseInt(xy[1]);
k = Integer.parseInt(br.readLine());
b = Integer.parseInt(br.readLine());
System.out.println(dp(y) - dp(x - 1));
}
private static int dp(int n) {
if(n == 0) return 0;
int cnt = 0;
while(n != 0) { //把B进制的每一位抠出来
a[++cnt] = n % b;
n = n / b;
}
int res = 0,last = 0; //last用来统计第i位之前已经放了几个1
for(int i = cnt; i >= 1; i--) { //从高位开始处理
int x =a[i]; //取出第i位的数
if(x != 0) { //第i位位0的话直接跳过即可
res += f[i-1][k-last];//第i位放0
if(x > 1) {//第i位>1
if(k - last - 1 >= 0) {
res += f[i-1][k-last-1];
}
break;//第i位放大于1的数,不合要求
}else { //x=1,不可以用组合数,继续枚举下一位
last++;
if(last > k) break;
}
}
if(i == 1 && last == k) res++;//特判,走到末位的情况
}
return res;
}
private static void init() { //预处理组合数
for(int i = 0; i < N; i++) f[i][0] = 1;
for(int i = 1; i < N; i++) {
for(int j = 1; j <= i; j++) {
f[i][j] = f[i-1][j-1] + f[i-1][j];
}
}
// for(int i = 0; i < N; i++) {
// for(int j = 0; j <= i; j++) {
// System.out.printf("f[%d %d]=%d\n",i,j,f[i][j]);
// }
// }
}
}
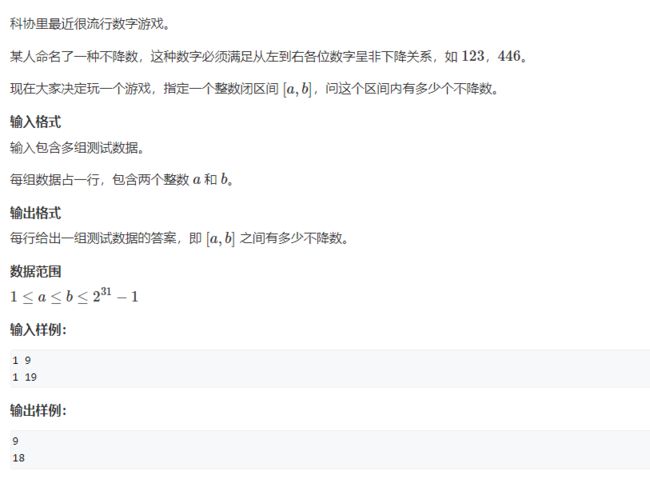
数字游戏
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int N = 12;
static int n = 0,q = 0;
static int[] a = new int[N];
static int[][] f = new int[N][N]; //f[i][j]表示一共有i位且最高数字位j的不降数个数
static int l = 0, r = 0;
public static void main(String[] args) throws Exception{
init();
String str = "";
while((str = br.readLine()) != null) {
String[] lr = str.split(" ");
l = Integer.parseInt(lr[0]);
r = Integer.parseInt(lr[1]);
System.out.println(dp(r) - dp(l - 1));
}
}
private static int dp(int n) {
if(n == 0) return 1;
int cnt = 0;
while(n != 0) { //抠出来每一位
a[++cnt] = n % 10;
n /= 10;
}
int res = 0,last = 0;
for(int i = cnt; i >= 1; i--) {//位数
int now = a[i];
for(int j = last; j < now; j++) {
res += f[i][j];
}
if(now < last) break;
last = now;
if(i == 1) { //走到a1的情况
res++;
}
}
return res;
}
private static void init() { //预处理
for(int i = 0; i <= 9; i++) f[1][i] = 1;
for(int i = 2; i < N; i++) { //位数
for(int j = 0; j <= 9; j++) { //最高位
for(int k = j; k <= 9; k++) { //次高位
f[i][j] += f[i-1][k];
}
}
}
// for(int i = 0; i < N; i++) {
// for(int j = 0; j <= i; j++) {
// System.out.printf("f[%d %d]=%d\n",i,j,f[i][j]);
// }
// }
}
}
Windy数
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
static int N = 12;
static int n = 0,q = 0;
static int[] a = new int[N];
static int[][] f = new int[N][10]; //f[i][j]表示一共有i位且最高数字位j的windy数的个数
static int l = 0, r = 0;
public static void main(String[] args) throws Exception{
init();
String[] lr = br.readLine().split(" ");
l = Integer.parseInt(lr[0]);
r = Integer.parseInt(lr[1]);
System.out.println(dp(r) - dp(l - 1));
}
private static int dp(int n) {
if(n == 0) return 0;
int cnt = 0;
while(n != 0) { //抠出来每一位
a[++cnt] = n % 10;
n /= 10;
}
//答案是cnt位
int res = 0,last = -2; //last表示上一位
for(int i = cnt; i >= 1; i--) {//位数
int now = a[i];
int st = 0;
if(i==cnt) {st = 1;} //不能有前导0
for(int j = st; j < now; j++) {
if(Math.abs(j - last) >= 2) {
res += f[i][j];
}
}
if(Math.abs(now - last) < 2) break;
last = now;
if(i == 1) res ++;
}
//答案小于cnt位的
for(int i = 1; i < cnt; i++) {
for(int j = 1; j <= 9; j++) {
res += f[i][j];
}
}
return res;
}
private static void init() { //预处理
for(int i = 0; i <= 9; i++) f[1][i] = 1;
for(int i = 2; i < N; i++) { //位数
for(int j = 0; j <= 9; j++) { //枚举第i位
for(int k = 0; k <= 9; k++) { //枚举第i-1位
if(Math.abs(k - j) >= 2) {
f[i][j] += f[i - 1][k];
}
}
}
}
//
// for(int i = 0; i < N; i++) {
// for(int j = 0; j <= i; j++) {
// System.out.printf("f[%d %d]=%d\n",i,j,f[i][j]);
// }
// }
}
}