基于灰狼优化算法(GWO)解决柔性作业车间调度问题(Matlab代码实现)
欢迎来到本博客❤️❤️
博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
本文目录如下:
目录
1 概述
2 运行结果
3 参考文献
4 Matlab代码实现
1 概述
基于GWO算法(灰狼优化算法)解决柔性作业车间调度问题是一种优化算法的应用。柔性作业车间调度问题是指在柔性制造系统中,将一组任务分配给一组机器,并决定任务的执行顺序和时间,以最小化某个优化目标,如总完成时间、平均完成时间等。
以下是基于GWO算法解决柔性作业车间调度问题的步骤:
问题建模:将柔性作业车间调度问题转化为数学模型,定义目标函数和约束条件。目标函数通常是要最小化的调度指标,例如总完成时间或平均完成时间。
初始化种群:使用GWO算法初始化一定数量的灰狼个体作为初始种群。每个个体表示一个可能的调度解,即柔性作业车间调度方案。
适应度计算:根据目标函数,计算每个个体的适应度值,用于衡量调度方案的优劣。
灰狼行为模拟:根据GWO算法中灰狼之间的模拟行为,进行搜索和优化。灰狼个体之间通过模拟领袖灰狼的位置来调整自己的位置,以寻找更优的解。
更新位置:根据模拟行为的结果,更新灰狼个体的位置和速度。这样,种群中的个体逐渐向更优的调度解靠近。
终止条件:设置终止条件,例如达到最大迭代次数或找到满意的调度解。
输出结果:在迭代过程中选择适应度最好的个体作为最终的调度解,输出调度方案及其优化结果。
需要注意的是,GWO算法作为一种全局优化算法,能够在搜索空间中较为广泛地探索解空间,有助于找到较好的调度解。然而,在应用GWO算法解决柔性作业车间调度问题时,需要根据具体问题进行适当的参数设置和优化策略,以获得较好的调度性能。
最终的结果还取决于问题的复杂程度、目标函数的设计和数据的特性。因此,在实际应用中,可能需要进行多次实验和调优,以选择最佳的参数和得到最优的调度方案。同时,建议参考相关研究论文和文献,以了解更多有关GWO算法在柔性作业车间调度问题中的应用和改进方法。
2 运行结果
主函数部分代码:
%该程序用于解决柔性作业车间调度,m个工件,n道工序,其中n为最大工序数,工件的工序
%数可以少于n,加工机器数为M,每个工件的每道工序具有多个机器可以选择,对应的时间
%不同,其中初始种群的储存方式采用cell数据类型
%Version:1.3
%fileDescription:调度机器可选的柔性作业车间问题,甘特图已完善,GWO,8*8实例
%last edit time:2019-6-7
function GWO_Model_FJSP_1_3_8_8()
count = 5000; %迭代次数
N = 100; %种群规模
m = 6; %工件数
n = 4; %工序数
M = 4; %机器数
a =2; %计算A/C协同系数的
plotif = 1; %控制程序是否进行绘图
s = input(m,n); %数据输入
[p,TN] = initial_p(m,n,N,s,M); %生成初始种群50,采用细胞结构,每个元素为8*4
P = machine(n,M);
FIT = zeros(count,1);
aveFIT = zeros(count,1);
X1=randperm(count); %收敛图形的横坐标X
X=sort(X1);
%------------------------输出最优解的时有用------------------------------
best_fit = 1000; %改变模型需要修改此参数
best_p = zeros(m,n);
best_TN = zeros(m,n);
Y1p = zeros(m,1);
Y2p = zeros(m,1);
Y3p = zeros(m,1);
minfit3 = 1000000000;
%-------------------------进行迭代--------------------------------------
for i = 1:count
[fit,Y1,Y2,Y3] = object(p,TN,N,P,m,n);
[newp,newTN] = GWO(fit,p,TN,N,m,n,s,a);
a = a-2/(count-1); %a的值会线性下降
if best_fit > min(fit)
[best_p,best_TN,best_fit,Y1p,Y2p,Y3p]=best(best_fit,best_p,fit,best_TN,Y1p,Y2p,Y3p,p,TN,Y1,Y2,Y3);
end
p = newp;
TN = newTN;
minfit = min(fit);
if minfit3>minfit
minfit3 = minfit;
end
FIT(i) = minfit3; %用于适应度函数的
aveFIT(i) = mean(fit); %用于适应度函数的
end
%------------------投射最佳方案数据--------------------------------------
fprintf('最优解:%d\n',best_fit);
fprintf('工序1 工序2 工序3 工序4\n');
best_p
fprintf('时间1 时间2 时间3 时间4\n');
best_TN
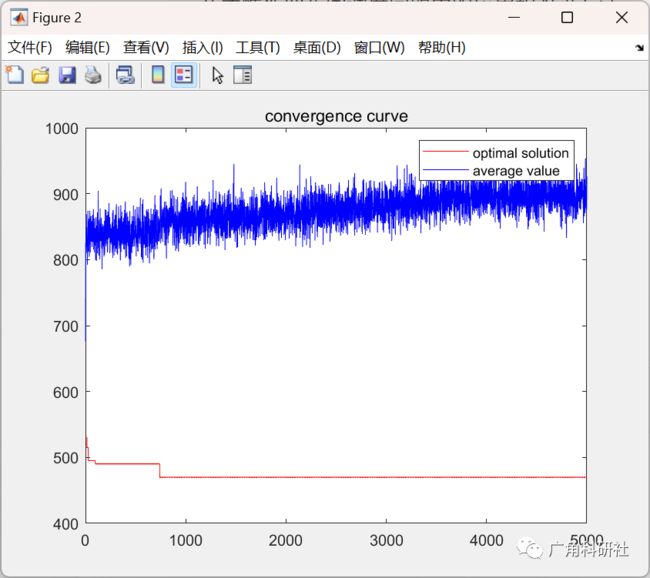
%------------------------收敛曲线----------------------------------------
if plotif == 1
figure;
plot(X,FIT,'r');
hold on;
plot(X,aveFIT,'b');
title('convergence curve');
hold on;
legend('optimal solution','average value');
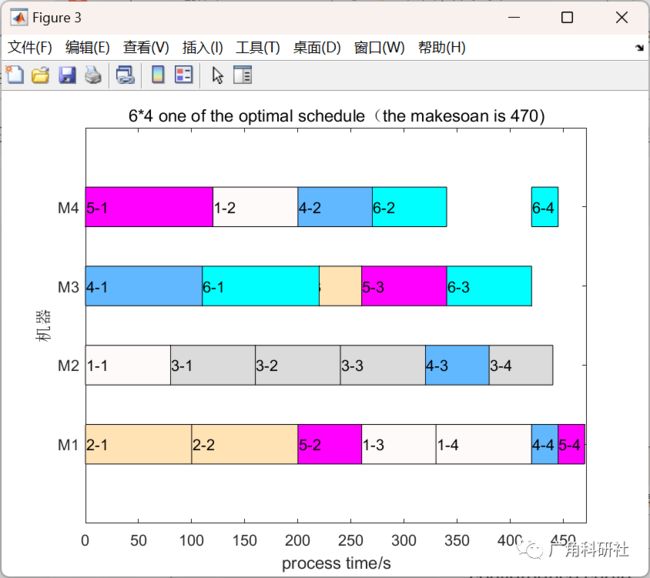
%-------------------------甘特图-----------------------------------------
figure;
w=0.5; %横条宽度
set(gcf,'color','w'); %图的背景设为白色
for i = 1:m
for j = 1:n
color=[1,0.98,0.98;1,0.89,0.71;0.86,0.86,0.86;0.38,0.72,1;1,0,1;0,1,1;0,1,0.49;1,0.87,0.67;0.39,0.58,0.92;0.56,0.73,0.56];
a = [Y1p(i,j),Y2p(i,j)];
x=a(1,[1 1 2 2]); %设置小图框四个点的x坐标
y=Y3p(i,j)+[-w/2 w/2 w/2 -w/2]; %设置小图框四个点的y坐标
color = [color(i,1),color(i,2),color(i,3)];
p=patch('xdata',x,'ydata',y,'facecolor',color,'edgecolor','k'); %facecolor为填充颜色,edgecolor为图框颜色
text(a(1,1)+0.5,Y3p(i,j),[num2str(i),'-',num2str(j)]); %显示小图框里的数字位置和数值
end
end
xlabel('process time/s'); %横坐标名称
ylabel('机器'); %纵坐标名称
title({[num2str(m),'*',num2str(M),' one of the optimal schedule(the makesoan is ',num2str(best_fit),')']}); %图形名称
axis([0,best_fit+2,0,M+1]); %x轴,y轴的范围
set(gca,'Box','on'); %显示图形边框
set(gca,'YTick',0:M+1); %y轴的增长幅度
set(gca,'YTickLabel',{'';num2str((1:M)','M%d');''}); %显示机器号
hold on;
end
%--------------------------输入数据---------------------------------
function s = input(m,n) %输入数据
s = cell(m,n);
s{1,1}=[1 2 3 4;100 80 110 120];
s{1,2}=[1 2 3 4;60 80 90 70];
s{1,3}=[1 2 3 4;90 60 80 100];
s{1,4}=[1 2 3 4;25 10 10 25];
s{2,1}=[1 2 3 4;100 80 110 120];
s{2,2}=[1 2 3 4;60 80 90 70];
s{2,3}=[1 2 3 4;90 60 80 100];
s{2,4}=[1 2 3 4;25 10 10 25];
s{3,1}=[1 2 3 4;100 80 110 120];
s{3,2}=[1 2 3 4;60 80 90 70];
s{3,3}=[1 2 3 4;90 60 80 100];
s{3,4}=[1 2 3 4;25 10 10 25];
s{4,1}=[1 2 3 4;100 80 110 120];
s{4,2}=[1 2 3 4;60 80 90 70];
s{4,3}=[1 2 3 4;90 60 80 100];
s{4,4}=[1 2 3 4;25 10 10 25];
s{5,1}=[1 2 3 4;100 80 110 120];
s{5,2}=[1 2 3 4;60 80 90 70];
s{5,3}=[1 2 3 4;90 60 80 100];
s{5,4}=[1 2 3 4;25 10 10 25];
s{6,1}=[1 2 3 4;100 80 110 120];
s{6,2}=[1 2 3 4;60 80 90 70];
s{6,3}=[1 2 3 4;90 60 80 100];
s{6,4}=[1 2 3 4;25 10 10 25];
%---------------------------建立初始种群-----------------------------
function [p,TN] = initial_p(m,n,N,s,M) %建立初始种群
p = cell(N,1); %p为初始解集的机器集
TN = cell(N,1); %TN为初始解集的时间集
for i = 1:N %产生N个初始解
store_m = zeros(M,1); %用于储存生成初始方案时的各机器数量
pz = zeros(m,n); %pz为中间储存量,用于储存解i的机器号,大小为m*n
tz = zeros(m,n); %tz为中间储存量,用于储存解i的加工时间,大小为m*n
for j = 1:m
for k = 1:n
sle = s(j,k); %sle为工件j的工序k的数据,第一行为可选机器数,第二行为对应的加工时间
sle2 = cell2mat(sle); %sle为cell结构,需要将sle用cell2mat函数转换为double类型
b = size(sle2,2); %数据中有0数组,所以需要判断
if b == 0
pz(j,k) = 0;
tz(j,k) = 0;
else
c = randperm(b,1); %产生一个1到b的随机数,用于选择机器
if store_m(c) >= (m*n)/M
c = randperm(b,1);
if store_m(c) >= (m*n)/M
c = randperm(b,1);
if store_m(c) >= (m*n)/M
c = randperm(b,1);
end
end
end
store_m(c) = store_m(c)+1;
pz(j,k) = sle2(1,c); %将机器赋予pz(j,k)
tz(j,k) = sle2(2,c); %将加工时间赋予tz(j,k)
end
end
end
p{i} = pz;
TN{i} = tz;
end
3 参考文献
[1]刘琼,张超勇,饶运清等.改进遗传算法解决柔性作业车间调度问题[J].工业工程与管理,2009,14(02):59-66.
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。