第三章 图论 No.1单源最短路及其综合应用
文章目录
-
-
- 1129. 热浪
- 1128. 信使
- 1127. 香甜的黄油
- 1126. 最小花费
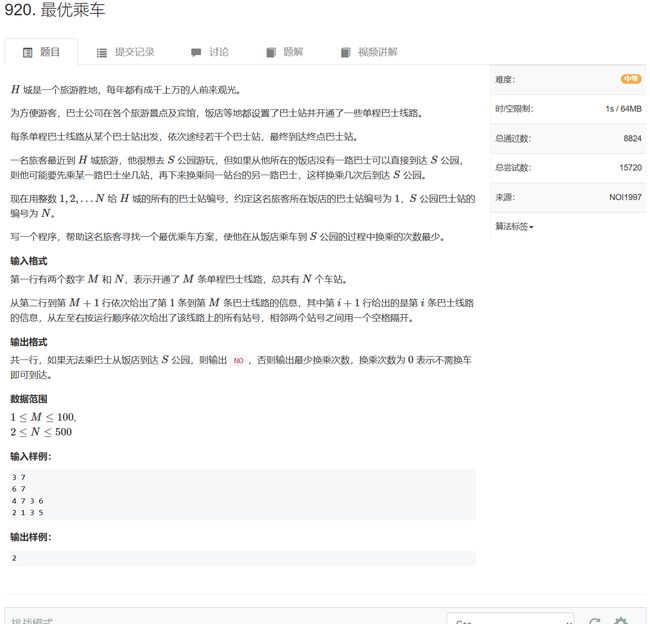
- 920. 最优乘车
- 903. 昂贵的聘礼
- 1135. 新年好
- 340. 通信线路
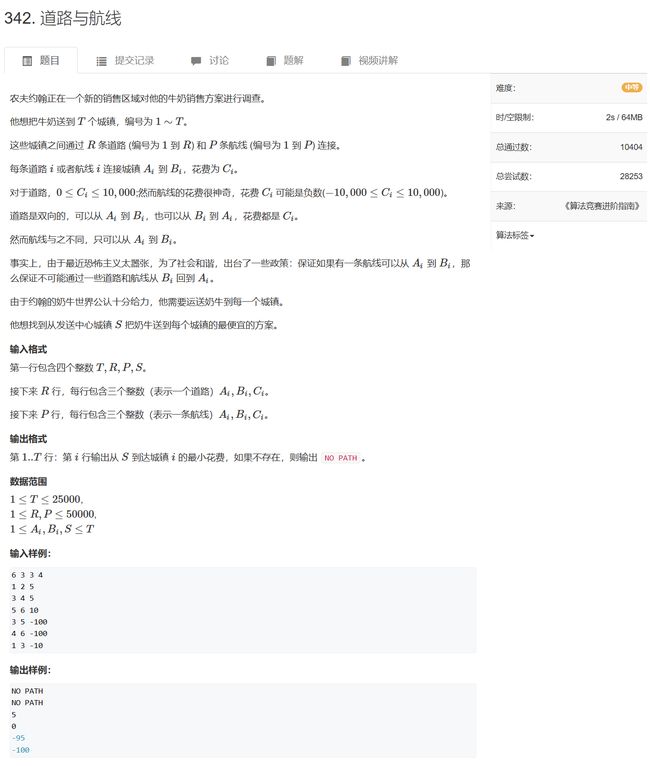
- 342. 道路与航线
- 341. 最优贸易
-
做乘法的最短路时,若权值>=0,只能用spfa来做,相等于加法中的负权边
1129. 热浪
单源最短路,稀疏图,用堆优化Dijkstra即可,就是板子套了个背景
// 稀疏图,用堆优化Dijkstra存储
#include debug:由于是无向图,边的数量要开两倍。但是w[N]没改,debug了很久
所以e[M], ne[M], w[M],只有h[N],其他的数组存储的都是边
1128. 信使
单源最短路,稀疏图,用堆优化Dijkstra即可,最后统计所有dis的最大值并返回即可
// 单源最短路,最后将第1个点到其他点的距离累加即可
// 稀疏图,依然是堆优化的dijkstra
#include debug:%d打成了5d,乐,竟然能编译通过
判断某个点的最短距离是否已经确定,打成了if(dis[x]); dis[x] = true,这也debug了半天
1127. 香甜的黄油
// 多源汇最短路,由于flody可能超时,所以用单源最短路求解
// 这里用spfa
#include 用自己写的循环队列代替queue,时间大概快了一倍
需要注意的是,循环队列的hh和tt从0开始使用,并且都是后置++,++后还要维护循环性质
以下是用queue实现的版本
// 多源汇最短路,由于flody可能超时,所以用单源最短路求解
// 这里用spfa
#include 1126. 最小花费
转账金额A,当手续费的比例为z时,只能转账A(1 - z)
若每条边的权值为实际转账的金额比例,那么从起点到终点,这个比例越大,花费的初始金额就越少,所以这题需要找一条从起点到终点比例最大的路径
即从起点到终点经过的所有边的比例相乘最大,由于比例的大小为 0 < z < = 1 0 < z <= 1 0<z<=1,所以这里初始化dis数组以及邻接矩阵为全0
接着用spfa或者dijkstra求“最短路”即可
// 同样的单源最短路,spfa解决
#include 920. 最优乘车
没之前的题目裸,需要一些思考
虽然题目没有给定边的权重,但是给定了公交路线,可知公交路线 a a a中, a i a_i ai到 a j a_j aj的权重为1,表示从i地到j地需要的乘车次数,当如 a i a_i ai在 a a a中的下标要出现在 a j a_j aj之前,这是一张有向图
所以,根据题目给定的公交路线,找出图中所有的有向边,最后用单源最短路就行了
由于边的权值为1,甚至用bfs也行
// 一条路线之间的点可达,存在有向边,线路中有n个点,存在Cn2条边
// 边的权值为1,表示需要乘车的次数,由于权值为1,所以可以用bfs
#include 903. 昂贵的聘礼
以下是我的思路,我只是记录一下不建议看
要获得某个物品,有两种方式:1. 直接购买 2. 在拥有替代品的前提下,以优惠价格购买
此外无法找出其他方法,需要考虑的是:以优惠价格购买时,拥有替代品的代价是什么?
若从正面考虑,假设酋长的10000金币是一个物品,现可以直接购买或者使用替代品。若使用替代品以更低的价格购买,那么购买替代品的价格是多少?同样,购买替代品也有两种方式,是直接购买省钱还是用替代品的替代品购买省钱。这是一个无止尽的过程,什么时候会停止?物品没有替代品时停止,这就意味着我们要递归到最底部后,在向上回溯的过程中,才能计算两种方式中哪种最省钱
这是直接的思路,可能能做出来吧,没试过
正解:
将酋长的10000金币看成物品,并且是有向图的终点。物品之间有什么关系?从一个点走到另一个点,前提是当前点是下一点的替代品,那么从当前点到下一点的代价就是用当前物品购买下一物品的优惠价格
所以边的权重为优惠价格,当前除了以优惠价格购买,还能直接购买。直接购买时,当前点的含义不再是一个物品,所以这里的点是一个虚拟点,到其他点的权重为直接购买的价格
若当前已经购买了物品,走向下一物品时,直接购买的价格肯定比使用替代品高,所以不用设置已经购买物品时,再直接购买其他物品的边。这样的边没有意义
由于存在一些物品无法使用替代品购买,所以只要设置手上没有物品时,直接购买物品的边

虚拟点为上图的s
起点为s,终点为1号物品(酋长的10000金币),跑一个最短路即可
为什么起点是s?存在一些只能直接购买的物品
最后考虑等级限制,等级差距不超过m的人可以交换物品,由于题目数据量小,可以直接暴力枚举。假设酋长的等级为a,那么需要枚举的区间为 [ a − m , a + m ] [a-m, a+m] [a−m,a+m],枚举这个区间中长度为m的区间,每次枚举跑一次最短路即可
#include 1135. 新年好
先用堆优dijkstra跑单源最短路,一共是6个源点,分别是家所在的点以及亲戚所在的点,保存最短距离
然后dfs爆搜,以1号点为起点,剩下五个点的全排列为搜索顺序,记录全排列中路径的最短距离
#include debug:双向边,M又少开一倍,但是TLE,以后M都开两倍吧,这太难调试了
dfs最后要返回res,因为min要使用dfs的返回值
340. 通信线路
分析题意:对于每条1~n的路径,我们只要支付第k+1大的边的金额即可。若边的数量少于k+1,那么支付金额为0
所以本题的最短路,短在第k+1大的边权中,最小的那个。所有最大中找最小,自然地想到二分。二分边权,得到ans,使得ans是所有1~n路径中,第k+1大的权值中最小的那个
二分的范围: [ 0 , 1 e 6 + 1 ] [0, 1e6+1] [0,1e6+1],权值最小值-1~权值最大值+1
check:分析ans的性质,所有1~n的路径中,第k+1大的边权中最小值为ans
说明至少存在一条路径,经过了k条边权大于ans的边,即and是这条路径中第k+1大的边
那么其他路径就一定经过了多于k条权值大于ans的边
由此得到check的检查逻辑:根据参数x,判断1~n的所有路径中,是否存在一条路径,经过了小于等于k条的权值大于x的边。若存在返回true,否则返回false
试想一下,x越大,check的性质越容易满足,x越小,性质越难满足
两种特殊情况:ans为0,说明1~n的所有路径中,至少存在一条路径,经过了k条权值大于0的边,那么第k+1条边的权值为0,需要支付金额为0
ans为 1 e 6 + 1 1e6+1 1e6+1,说明1n的所有路径中,至少存在一条路径,经过了k条权值大于$1e6+1$的边,由于边权最大为$1e6$,所以这样的路径是不存在的,即1n之间不连通
如何得知1~n的所有路径中,经过了几条权值大于x的边?
对于权值大于x的边,将其权值设置为1,否则设置为0,跑一遍最短路,就能知道1~n的最短路径经过了几条权值大于x的边
对于权值只有0和1的最短路问题,可以用双端队列bfs
#include 342. 道路与航线
直接用spfa会被卡两个数据
根据题意:道路,双向边,存在环,正权;航线:单向边,无环,负权
其中关于是否有环以及权值的正负是选择算法的关键
若图中没有负权边,直接用堆d
若图中无环,直接按照拓扑序遍历所有点就能确定最短路
结合以上两者,可以得到以下算法:
将所有点根据道路的连通性分成多个连通块,每个连通块之间不连通
连通每个连通块的是航线,单向边。读取所有的航线后,按照拓扑序遍历每个连通块,对于每个连通块,跑堆d求最短路
用id数组表示每个点所属的连通块编号,用二维数组blocks存储每个连通块中点的编号
读入所有道路后,dfs可以遍历连通块中的所有点,维护出id和blocks数组信息
读入所有航线,维护出in数组,计算所有点的入度后按照拓扑序跑堆d
// 道路是双向的,航线单向,可能是负数也可能是正数
// 并且图中保证不会存在环路
// 直接spfa?
#include 341. 最优贸易
状态表示:
集合:所有从1~n的路径,用分界点将这些路径一分为二
属性:在分界点之前(包括分界点)买入 - 在分界点(包括分界点)之后能卖出的最大价值,即最大卖出价值 - 最小买入价值
f ( i ) f(i) f(i)表示以i号点为分界点的1~n路径中,可以赚取的最大价值
状态划分:分界点从1~n,此时划分的子集不遗漏地组成了整个集合(虽然有重复,但是题目要求最优解,重复的情况不影响最优解)
如何求路径中的前半段最小值 d m i n ( k ) dmin(k) dmin(k)?
若与k直接相连的点有t个,那么 d m i n ( k ) = m i n ( d m i n ( s 1 ) , d m i n ( s 2 ) , . . . d m i n ( s t ) , w k ) dmin(k) = min(dmin(s_1), dmin(s_2), ... dmin(s_t), w_k) dmin(k)=min(dmin(s1),dmin(s2),...dmin(st),wk)
走到k的最小值就等于从所有走到与k直接相连的点的最小值以及自己的权值中的最小值
由于这些状态依赖可能存在环,即当dp推导出的状态不是最优解,所以这里用最短路求这些状态
最短路用dijkstra或者spfa,是否能用dijkstra?由于在最短路问题中,当前点的最短路径由与之相连的所有点的最短路径累加上自己的权值确定,并且权值只能是正的
根据这个性质,已经确定最短路的点在之后的更新中不可能出现更短的路径
虽然这题的边权为正,但是这题的状态不是由之前的状态累加,而是从之前的状态中取min或者max,这就导致dijkstra每次的更新无法求得最优解,需要后续的再次更新,此时的时间复杂度无法保证,这是最关键的,所以不使用dijkstra
那spfa呢?spfa是bellman-ford的优化,bellman根据边的数量进行更新,每次更新所有边
所以bellman能够保证最短路的边数,即时间复杂度是确定的,所以可以使用sfpa
用sfpa跑出dmin和dmax数组的信息,分别存储了从1到k的最小值,以及从k到n的最大值
由于从k到n的起点是变化的,但是终点不变,所以这里可以建一张反向图,以n为起点,更新dmax
#include