第四章 No.1树状数组的原理与使用
文章目录
-
- 应用问题
- 原理
- 树状数组练习题
-
- 241. 楼兰图腾
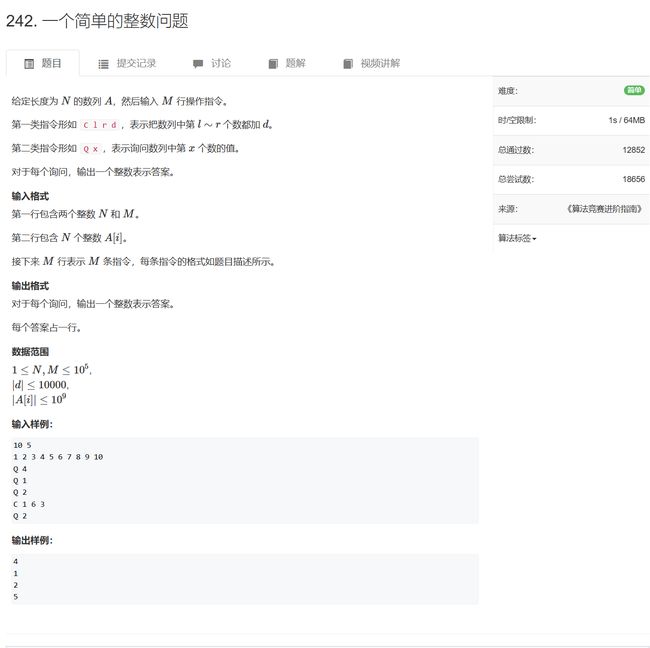
- 242. 一个简单的整数问题
- 243. 一个简单的整数问题2
- 244. 谜一样的牛
线段树的反面:树状数组原理复杂,实现简单
应用问题
支持两个操作:快速求前缀和任意地修改某个数,时间复杂度为 O ( l o g n ) O(logn) O(logn)
用前缀和数组,求前缀和的复杂度为 O ( 1 ) O(1) O(1),但是任意修改某个数的复杂度为 O ( n ) O(n) O(n)
用数组,求前缀和的复杂度为 O ( n ) O(n) O(n),修改某个数的时间复杂度为 O ( 1 ) O(1) O(1)
而使用树状数组,可以以适中的时间复杂度解决以上问题
原理
原理就是二进制表示,一个整数x,将其二进制表示后,可以直观地发现该数可以表示成多个2的幂相加
比如10110可以表示成: 2 1 + 2 2 + 2 4 2^1+2^2+2^4 21+22+24
在最坏情况下,一个32位整数n需要将32个2的幂相加,即 O ( l o g n ) O(logn) O(logn)
分析一下:将1~x整个区间划分后,每个子区间是怎样的?

每一个区间长度都为2的幂
第一个区间为 ( x − 2 i 1 , x ] (x-2^{i_1}, x] (x−2i1,x],长度为 2 i 1 2^{i_1} 2i1
第二个区间为 ( x − 2 i 1 − 2 i 2 , x − 2 i 1 ] (x-2^{i_1}-2^{i_2}, x-2^{i_1}] (x−2i1−2i2,x−2i1],长度为 2 i 2 2^{i_2} 2i2
…
最后一个区间为 ( 0 , x − 2 i 1 − 2 i 2 − . . . − 2 i k − 1 ] (0, x-2^{i_1}-2^{i_2}-...-2^{i_{k-1}}] (0,x−2i1−2i2−...−2ik−1],长度为 2 i k 2^{i_k} 2ik
其中k为x中1的个数
可以发现,区间 ( l , r ] (l, r] (l,r]可以表示成 [ r − l o w b i t ( r ) + 1 , r ] [r-lowbit(r)+1, r] [r−lowbit(r)+1,r]
因为区间长度一定是r的最后一位1对应的幂,即lowbit(r)
假设数组长度为n,对于1~n之间的所有数,将其作为区间 [ r − l o w b i t ( r ) + 1 , r ] [r-lowbit(r)+1, r] [r−lowbit(r)+1,r]的右端点,则这些区间将有重复地覆盖1~n整个区间
长度为16的数组的划分:
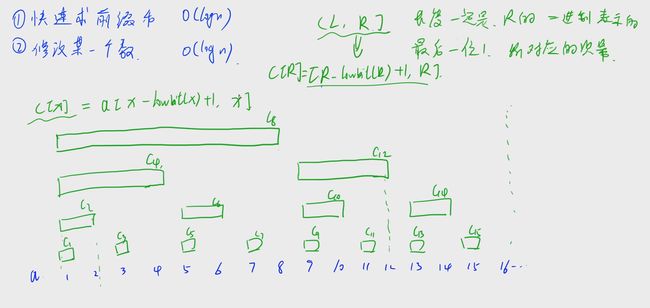
将每段区间看成节点,再看上面这张图
连接了存在关系的区间,那么所有区间就构成了一颗树。这便是树状数组名字的由来,十分的形象,思考父子节点之间的关系
对于 C 16 C_{16} C16这个区间,它由 ( a 16 , C 15 , C 14 , C 12 , C 8 ) (a_{16}, C_{15}, C_{14}, C_{12}, C_{8}) (a16,C15,C14,C12,C8)组成,再举例几个区间后
可以看出规律:区间 C n C_n Cn由区间 ( a n , C . . . ) (a_n, C...) (an,C...)组成,其中除了 a n a_n an,剩下区间的下标k加上lowbit(k)后的结果为16
15:01111 + 1 = 10000,01111 - 1 = 01110
14:01110 + 10 = 10000,01110 - 10 = 01100
12:01100 + 100 = 10000,01100 - 100 = 01000
8:01000 + 1000 = 10000,01000 - 1000 = 00000
观察这些下标k的规律,每次下标变小都是减去了lowbit(k),当下标为0,说明当前节点没有子节点了
通过以上推导,可以发现子节点下标到父节点下标的规律:
假设当前区间为 C x C_x Cx,那么 C x + l o w b i t ( x ) C_{x+lowbit(x)} Cx+lowbit(x)是其父节点, C x + l o w b i t ( l o w b i t ( x ) ) C_{x+lowbit(lowbit(x))} Cx+lowbit(lowbit(x))是其祖父节点…直到下标超过n。此时作为 C x C_x Cx的祖先节点不存在
为什么要知道子节点到父节点的关系?由于 C x C_x Cx维护着数组中的某段区间和,并且这些区间之间存在着重叠,修改数组中的任意一个数后,必定会向上影响其的父节点的区间和,此时只能通过子节点不断地更新到根节点,才能维护正确的数据。所以知道子节点到父节点的关系是有必要的
总结一下:
子节点到父节点的推导:假设子节点在数组中的下标为x,需要不断地对子节点的下标加上lowbit(x),获取其父节点的下标直到下标超过数组长度的最大值
由此就能实现修改任意位置的成员
// 对原数组x下标位置上的数+c
void add(int x, int c)
{
for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
其中tr数组是维护的树状数组
第二个问题:如何获取前缀和?
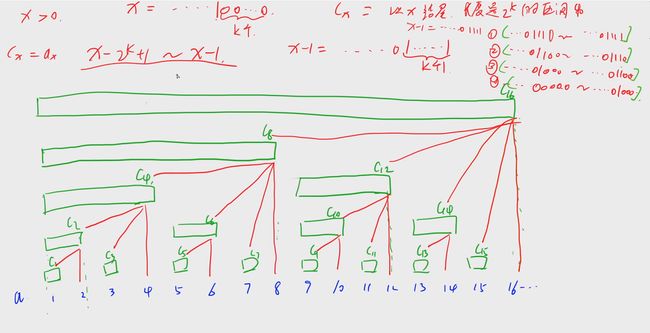
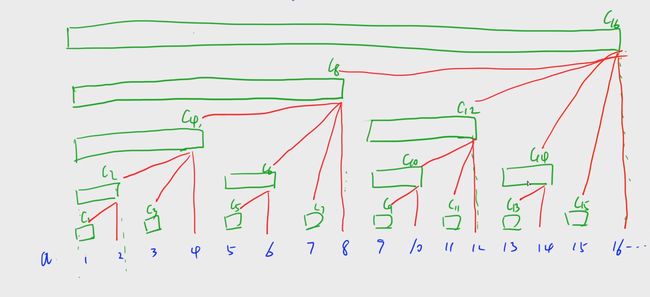
还是这张图,假设要获取前16个数的和,直接返回树状数组的 C 16 C_{16} C16即可,也就是树状数组的第16个成员
假设要获取前14个数的和,需要返回 C 14 + C 12 + C 8 C_{14}+C_{12}+C_8 C14+C12+C8,将它们的下标转换成二进制
001110
001100
001000
000000
可以发现,在整个数为0之前,二进制表示的最后一个1不断被减去
经过归纳,求前i个数的和时,需要对树状数组中的数进行累加,这些数的下标从i开始,不断地减去最后一位1,直到i为0
注意不要先减去1再不断减去lowbit(k),那是求节点的子节点方式
直接减去lowbit(k)是求前缀和的方式
int sum(int x)
{
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
如何建立数组数组?
建立树状数组的方式有两种,最简单的方式是直接调用add将需要修改的数添加(一开始树状数组的所有成员为0),时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)
此外,还能直接根据定义建数组,先求出原数组a[n]的前缀和数组s[n]
树状数组中,区间 ( r − l o w b i t ( r ) + 1 , r ) (r-lowbit(r)+1, r) (r−lowbit(r)+1,r)的值为s[r] - s[r - lowbit[r]],此时直接修改原数组即可
由于不用调用add,所以时间复杂度为 O ( n ) O(n) O(n),但该做法额外维护了一个前缀和数组
树状数组练习题
241. 楼兰图腾
划分所有的纵坐标成k个集合,每个集合表示纵坐标为 y k y_k yk时,能构成的v和∧的数量
( x , y k ) (x, y_k) (x,yk)能构成的v的数量:在横坐标小于x的坐标中,纵坐标大于 y k y_k yk的坐标数量乘以横坐标大于x的坐标中,纵坐标大于 y k y_k yk的坐标数量
( x , y k ) (x, y_k) (x,yk)能构成的∧的数量:在横坐标小于x的坐标中,纵坐标小于 y k y_k yk的坐标数量乘以横坐标大于x的坐标中,纵坐标小于 y k y_k yk的坐标数量
树状数组存储纵坐标小于等于当前下标的坐标数量,比如tr[i]表示纵坐标小于等于i的坐标数量
将所有纵坐标按照横坐标的升序顺序存储到数组a中,遍历a[i]时,需要求出纵坐标小于a[i]以及纵坐标大于a[i]的坐标数量,分别用l数组和g数组存储。这是横坐标小于x且纵坐标大于或小于a[i]的坐标数量,也就是前缀和
a[i]的前缀和求完后,需要将tr[a[i]]加1,表示纵坐标小于等于a[i]的坐标数量+1
前缀和求完后再求后缀和,便能得到答案
tr[i]存储纵坐标小于等于a[i]的坐标数量,如何求纵坐标小于a[i]的坐标数量?tr[a[i]-1]即可
如何求纵坐标大于a[i]的坐标数量,tr[max] - tr[a[i]]即可,max表示所有纵坐标中的最大值
#include 242. 一个简单的整数问题
将某段区间中的数加上c,而不是修改成c,使用差分数组可以完美解决此问题
查询原数组中某个数的值,使用差分数组需用 O ( n ) O(n) O(n),总的复杂度为 O ( n m ) O(nm) O(nm),可能会超时,所以考虑如何优化
通过差分数组求原数组的某个数其实是一个前缀和操作,要优化 O ( n ) O(n) O(n)的前缀和可以考虑树状数组。自然地,树状数组存储的是原数组的差分信息,1. 将区间 [ l , r ] [l, r] [l,r]加上c时,只用修改 l l l和 r + 1 r+1 r+1位置上的数即可,复杂度为 O ( l o g n ) O(logn) O(logn) 2. 求原数组的某个数时,使用树状数组的sum操作即可,时间复杂度为 O ( l o g n ) O(logn) O(logn)
总的时间复杂度为 O ( m l o g n ) O(mlogn) O(mlogn),不会超时
#include debug:add(l, d); add(r + 1, -d),后面那个add习惯地写成了add(r + 1, d)
以及可能存在的爆int问题,一直都没有特别注意
243. 一个简单的整数问题2
需要实现两个操作:1. 对区间中的所有数加上一个数 2. 求区间和
与上题思路类似,保存差分信息以实现第一个操作
求区间和时,思考如何求原数组中的某个数 a i a_i ai?这需要对差分数组前缀求和
那么如何求原数组中的区间和呢?分别求出区间中的每个数吗?就算对前缀和求解过程进行优化,也要 O ( n ) O(n) O(n)
思考如何优化对n个数求前缀和?如下图,列出 a [ 1 ] a[1] a[1]到 a [ x ] a[x] a[x]中的每个数需要的差分信息,补全这些差分信息(图中红蓝部分)

可以发现区间 ( 1 , x ) (1, x) (1,x)的和就是蓝色部分,等于所有的和减去红色的和
( b 1 + b 2 + . . . + b x ) ( x + 1 ) − ( 1 b 1 + 2 b 2 + . . . + x b x ) (b_1+b_2+...+b_x)(x+1)-(1b_1+2b_2+...+xb_x) (b1+b2+...+bx)(x+1)−(1b1+2b2+...+xbx)
就是 b i b_i bi的前缀和乘以 ( x + 1 ) (x+1) (x+1)再减去 i b i ib_i ibi的前缀和
b i b_i bi的前缀和可以通过树状数组tr1维护, i b i ib_i ibi的前缀和可以通过树状数组tr2维护
对于题目需要的两个操作,维护这两个数组可以实现第二个操作,同时tr1数组能实现第一个操作
#include debug:总是习惯LL用%d读取
244. 谜一样的牛
从最后一个数开始往前推,若 a n a_n an为 k k k,说明前面有k头身高低于第n头牛的牛,此时 a n a_n an为所有身高中第 k + 1 k+1 k+1小的数,将该身高删除,因为每头牛的身高不同
若 a i a_i ai为 k k k,说明 a i a_i ai为剩下的身高中第 k + 1 k+1 k+1小的数
综上,需要实现两个操作:1. 删除某个身高 2. 计算身高中第 k k k小的数
除了平衡树,树状数组也能实现这两个操作
因为每头牛的身高不同,所以1~n中的每个数只能使用一次,将数组 b [ n ] b[n] b[n]的所有成员初始化成1,表示每个身高都没有使用过。一旦使用了某个身高,对应位置上的成员-1,由此可以实现第一个操作
用树状数组维护 b [ n ] b[n] b[n]数组的前缀和,如何计算数组中第k小的身高?若sum(x) = i说明小于等于x的身高中,有i个升高没有被使用
只要找到第一个满足sum(x) = k的x即可,此时的x就是剩下身高中第k小的身高,这个用二分可以实现
#include