外部排序算法总结
一.内排总结
在之前博客里,博主已经介绍了各种内部排序算法的原理和C语言代码实现,不懂的朋友可以在同系列专栏里选择查看,今天介绍常见排序算法的最后一点,也就是外部排序。在此之前,我们先对外部排序的各种算法做一下简单的总结。
| 算法种类 | 时间复杂度(最好) | 时间复杂度(最坏) | 时间复杂度(平均) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 折半插入排序 | O(n) | O(n2 ) | O(n2 ) | O(1) | 是 |
| 直接插入排序 | O(n) | O(n2 ) | O(n2 ) | O(1) | 是 |
| 希尔排序 | ---- | ---- | ---- | O(1) | 否 |
| 冒泡排序 | O(n) | O(n2 ) | O(n2 ) | O(1) | 是 |
| 快速排序 | O(nlog2 n) | O(n2 ) | O(nlog2 n) | O(log2 n) | 否 |
| 简单选择排序 | O(n2 ) | O(n2 ) | O(n2 ) | O(1) | 否 |
| 堆排序 | O(nlog2 n) | O(nlog2 n) | O(nlog2 n) | O(1) | 否 |
| 2路归并排序 | O(nlog2 n) | O(nlog2 n) | O(nlog2 n) | O(n) | 是 |
| 基数排序 | O(d(n+r)) | O(d(n+r)) | O(d(n+r)) | O® | 是 |
针对每种排序算法的效率差别,我已经总结在上面的表格里了,同时我后面还写了一份针对408范围内的所有数据结果和算法的效率分析专项总结,大家可以期待一首。
二.外部排序
1.外排概念
前面介绍过的排序方法都是在内存中进行的(称为内部排序)。而在许多应用中,经常需要对大文件进行排序,因为文件中的记录很多,无法将整个文件复制进内存中进行排序。因此,需要将待排序的记录存储在外存上,排序时再把数据一部分一部分地调入内存进行排序,在排序过程中需要多次进行内存和外存之间的交换。这种排序方法就称为外部排序。
2.排序方法
文件通常是按块存储在磁盘上的,操作系统也是按块对磁盘上的信息进行读写的。因为磁盘读/写的机械动作所需的时间远远超过内存运算的时间(相比而言可以忽略不计),因此在外部排序过程中的时间代价主要考虑访问磁盘的次数,即I/O次数。
外部排序通常采用归并排序法。它包括两个阶段:①根据内存缓冲区大小,将外存上的文件分成若干长度为l的子文件,依次读入内存并利用内部排序方法对它们进行排序,并将排序后得到的有序子文件重新写回外存,称这些有序子文件为归并段或顺串;②对这些归并段进行逐趟归并,使归并段(有序子文件)逐渐由小到大,直至得到整个有序文件为止。
3.举例说明
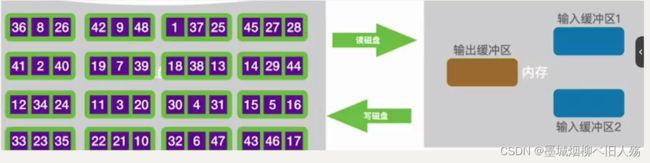
用上面这个例子来说明,我们假设左边是外存中的待排序序列,右边是我们的内存。(这里我们只是举例,实际上用到外部排序时,外存数据量非常庞大,这里只是演示。)这里涉及一部分操作系统的知识点,但都是计算机专业,应该都学过,内存的数据修改完之后是要写回外存的,所以我们这里有两个输入缓冲区和一个输出缓冲区,输入缓冲区用来读入磁盘数据,输出缓冲区用于把数据写回磁盘。
由于我们的外部排序是基于归并排序算法的,归并排序算法要求初始序列有序,所以这里我们在开始外部排序之前(或者说正式排序之前也就是叫预排序),我们需要构造初始有序序列。我们首先从磁盘读取两个块数据进入内存,然后在内存中对这两个块的数据进行某一种内部排序。
针对本例的前两个数据块,当排序结果写满一个输出缓冲区时,我们把输出缓冲区的数据写回外存。以此类推,预排序就是把外存的数据每两个块读入内存后排序,排序后写回结果。这里的几个块一读是基于内存中输入缓冲区的个数有关,它的选取和外部以及内部空间的大小有关。
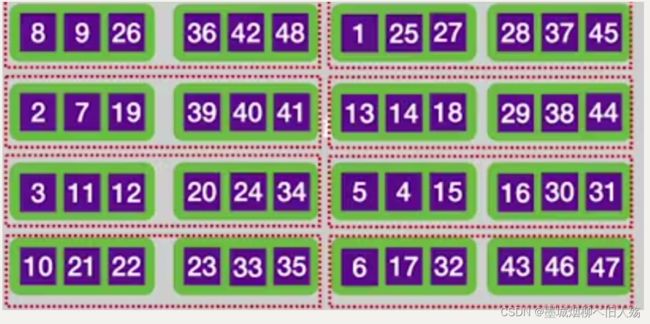
预排序后的结果应该是这样的:
接下来我们的外存中就存在初始有序序列了,所以可以开始进行正常的归并排序了。这里注意,预排序是两个数据块一读,所以两个数据块就形成了一个初始子序列哦,这里只有8个初始子序列哦。接下来把子序列1和子序列2的第一块分别读入输入缓冲区,开始内部排序,还是一样,输出缓冲区已满我们就写回外存。这里还有一点注意哦,当某个时刻比如输入缓冲区1的数据完了,我们不是把输入缓冲区2的数据直接填到输出缓冲区,而是把原来子序列后面的数据块读入内存哦(假设我们这里使用的内部排序算法也是归并排序),这样两个子序列是不是又合并成了一个大的子序列。然后两个大的子序列又可以合并成一个更大的序列,直到最后只有一个序列表示我们外部排序完成。
4.效率分析
我们应该知道,这里影响时间效率的最大因素其实是I/O口的读取次数,内部排序的时间相较于I/O口的读取的读取时间是很少的。所以如果我们想要提高外部排序的时间效率,那么就得想办法减少I/O口的读取次数。
一般地, 对r个初始归并段,做k路平衡归并,归并树可用严格k叉树(即只有度为k与度为0的结点的k叉树)来表示。第一趟可将r个初始归并段归并为 ⌈ r / k ⌉ \lceil{r/k}\rceil ⌈r/k⌉ 个归并段,以后每趟归并将m个归并段归并成 ⌈ m / k ⌉ \lceil{m/k}\rceil ⌈m/k⌉个归并段,直至最后形成一个大的归并段为止。树的高度-1 =「logr1=归并趟数S。可见,只要增大归并路数k,或减少初始归并段
个数r,都能减少归并趟数s,进而减少读写磁盘的次数,达到提高外部排序速度的目的。
三.败者树
上节讨论过,增加归并路数k能减少归并趟数s,进而减少I/O次数。然而,增加归并路数k时,内部归并的时间将增加。做内部归并时,在k个元素中选择关键字最小的记录需要比较k-1次。每趟归并n个元素需要做(n-1)(k-1)次比较,s趟归并总共需要的比较次数随k增长而增长。因此内部归并时间亦随k的增长而增长。这将抵消由于增大k而减少外存访问次数所得到的效益。因此,不能使用普通的内部归并排序算法。为了使内部归并不受k的增大的影响,引入了败者树。 败者树是树形选择排序的一种变体,可视为一棵完全二叉树。k个叶结点分别存放k个归并段在归并过程中当前参加比较的记录,内部结点用来记忆左右子树中的“失败者”,而让胜者往上继续进行比较,一直到根结点。若比较两个数,大的为失败者、小的为胜利者,则根结点指向的数为最小数。
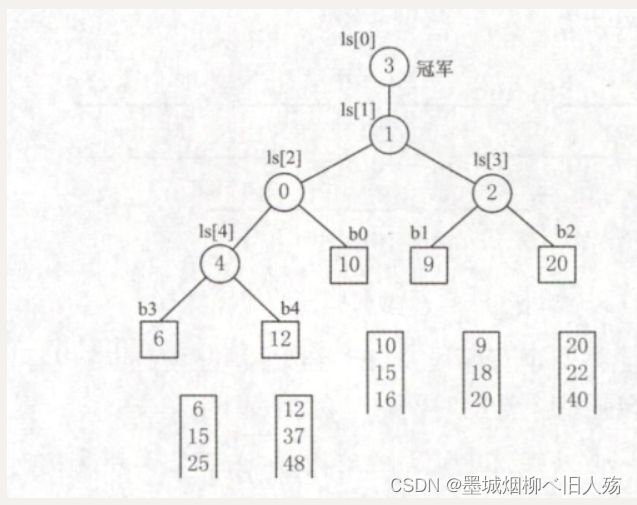
这是实现一个5路归并的败者树的例子。
可见,使用败者树后,内部归并的比较次数与k无关了。因此,只要内存空间允许,增大归并路数k将有效地减少归并树的高度,从而减少I/O次数,提高外部排序的速度。值得说明的是,归并路数k并不是越大越好。归并路数k增大时,相应地需要增加输入缓冲区的个数。若可供使用的内存空间不变,势必要减少每个输入缓冲区的容量,使得内存、外存交换数据的次数增大。当k值过大时,虽然归并趟数会减少,但读写外存的次数仍会增加。
四.置换-选择排序(生成初始序列)
减少初始归并段个数r也可以减少归并趟数S。若总的记录个数为n,每个归并段的长度为l,则归并段的个数r=「nll 1。采用内部排序方法得到的各个初始归并段长度都相同(除最后一段外),它依赖于内部排序时可用内存工作区的大小。因此,必须探索新的方法,用来产生更长的初始归并段,这就是本节要介绍的置换-选择算法。
设初始待排文件为FI,初始归并段输出文件为FO,内存工作区为WA, FO和WA的初始状态为空,WA可容纳w个记录。置换选择算法的步骤如下:
- 1)从FI输入w个记录到工作区WA。
- 2)从WA中选出其中关键字取最小值的记录,记为MINIMAX记录。
- 3)将MINIMAX记录输出到FO中去。
- 4)若FI不空,则从FI输入下一个记录到WA中。
- 5)从WA中所有关键字比MINIMAX记录的关键字大的记录中选出最小关键字记录,作为新的MINIMAX记录。
- 6)重复
3) ~5),直至在WA中选不出新的MINIMAX记录为止,由此得到一个初始归并段,输出一个归并段的结束标志到FO中去。 - 7)重复
2)~6),直至WA为空。由此得到全部初始归并段。
五.最佳归并树
文件经过置换-选择排序后,得到的是长度不等的初始归并段。下 面讨论如何组织长度不等的初始归并段的归并顺序,使得I/O次数最少?假设由置换选择得到9个初始归并段,其长度(记录数)依次为9, 30, 12, 18,3, 17,2,6,24。现做3路平衡归并,其归并树如图8.16所示。在图左中,各叶结点表示一个初始归并段,上面的权值表示该归并段的长度,叶结点到根,的路径长度表示其参加归并的趟数,各非叶结点代表归并成的新归并段,根结点表示最终生成的归并段。树的带权路径长度WPL为归并过程中的总读记录数,故I/O次数= 2xWPL = 484。
显然,归并方案不同,所得归并树亦不同,树的带权路径长度(I/O次数)亦不同。为了优化归并树的WPL,可以将哈夫曼树的思想推广到m叉树的情形,在归并树中,让记录数少的初始归并段最先归并,记录数多的初始归并段最晚归并,就可以建立总的I/O次数最少的最佳归并树。上述9个初始归并段可构造成一棵如图右所示的归并树,按此树进行归并,仅需对外存进行446次读/写,这棵归并树便称为最佳归并树。
六.总结
好了,到这里408范围内的数据结构和算法部分我们已经学完了,接下来转战计算机网络和操作系统部分。