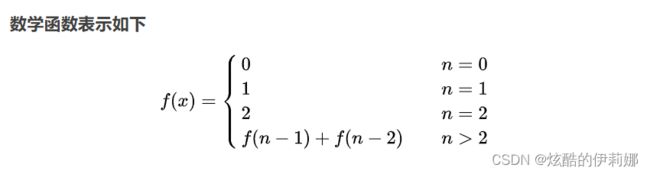【C语言】牛客网刷题训练-11
针对C语言入门OJ题牛客网 - 找工作神器|笔试题库|面试经验|实习招聘内推,求职就业一站解决_牛客网
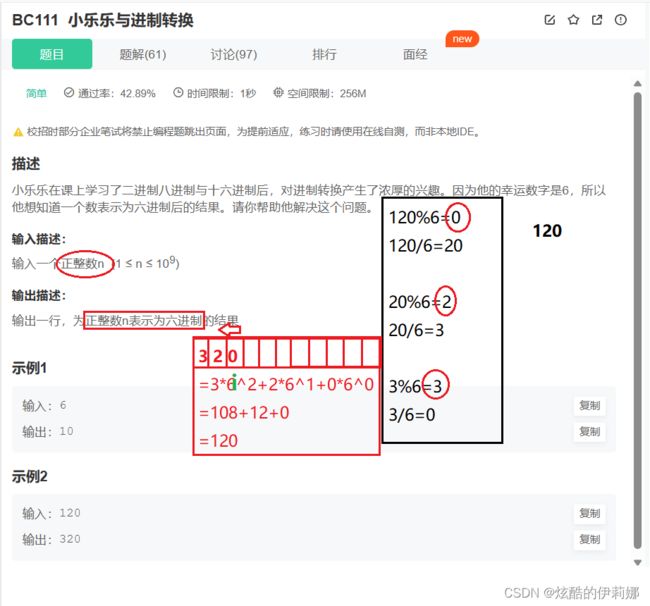
(简单)BC111-小乐乐与进制转换_牛客题霸_牛客网
参考代码:
#include
int main()
{
int n = 0;
int arr[40] = {0};//所给空间够用即可
int i = 0;
scanf("%d", &n);
while(n)
{
arr[i] = n%6;
i++;
n = n/6;
}
for(i--; i>=0; i--)
{
printf("%d", arr[i]);
}
return 0;
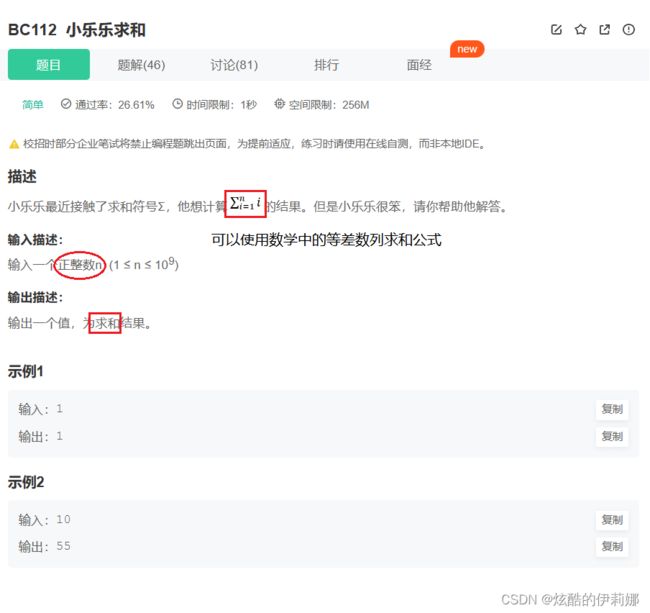
} (简单)BC112-小乐乐求和_牛客题霸_牛客网
参考代码:
#include
//代码1
int main()
{
long long i = 0;
long long sum = 0;
long long n = 0;
scanf("%lld", &n);
for(i=1; i<=n; i++)
{
sum += i;
}
printf("%lld\n", sum);
return 0;
} //代码2
int main()
{
long long n = 0;
scanf("%lld", &n);
printf("%lld", (1+n)*n/2);//等差数列求和公式
return 0;
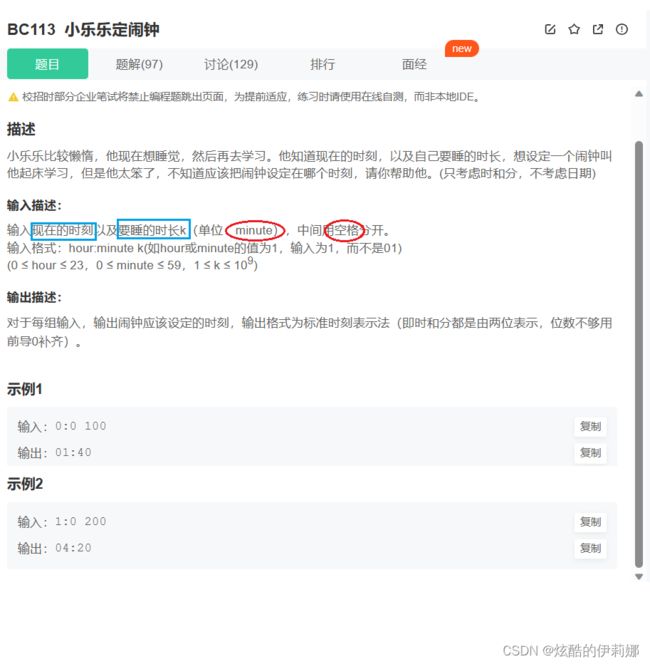
}(简单)BC113-小乐乐定闹钟_牛客题霸_牛客网
参考代码:
#include
int main()
{
int h = 0;//hour
int m = 0;//minute
int k = 0;//要睡的时长
scanf("%d:%d %d", &h, &m, &k);
//注意:这里要先算h,如果先算m,则会将赋值后的m代到h的公式中
h = ((m+k)/60+h)%24;//24进制
m = (m+k)%60;
printf("%02d:%02d\n", h, m);
return 0;
} (简单)BC114-小乐乐排电梯_牛客题霸_牛客网
参考代码:
#include
int main()
{
int n = 0;
scanf("%d", &n);
printf("%d\n", (n/12)*4+2);//每趟12人,一整趟4分钟,上去需要2分钟
return 0;
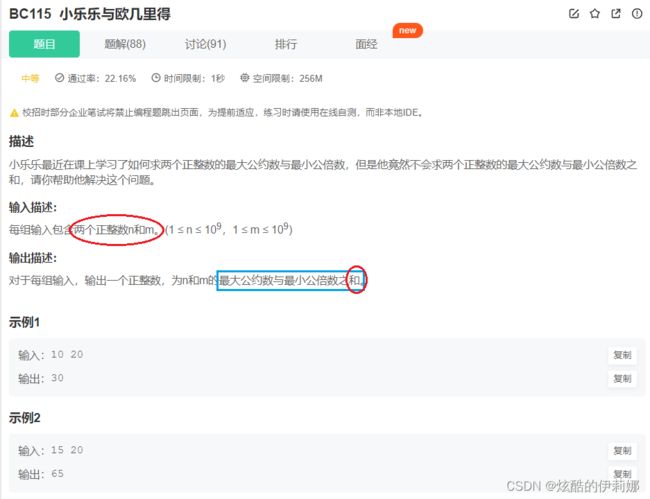
} (中等)BC115-小乐乐与欧几里得_牛客题霸_牛客网
参考代码:
#include
//暴力求解:
//耗时太久,无法满足条件
int main()
{
long long n = 0;
long long m = 0;
scanf("%lld %lld", &n, &m);
long long max = n>m?m:n;//假设n和m的较小值为最大公约数
while(max)
{
if(n%max==0 && m%max==0)
{
break;
}
max--;
}
long long min = m>n?n:m;//假设n和m的较大值为最小公倍数
while(min)
{
if(min%n==0 && min%m==0)
{
break;
}
min++;
}
printf("%lld\n", max+min);
return 0;
} //辗转相除法:
#include
int main()
{
long long n = 0;
long long m = 0;
long long tmp = 0;
scanf("%lld %lld", &n, &m);
int a = n;
int b = m;
while(tmp=a%b)
{
a = b;
b = tmp;
}
//b - 最大公约数
//n*m/b - 最小公倍数
printf("%lld\n", b+n*m/b);
return 0;
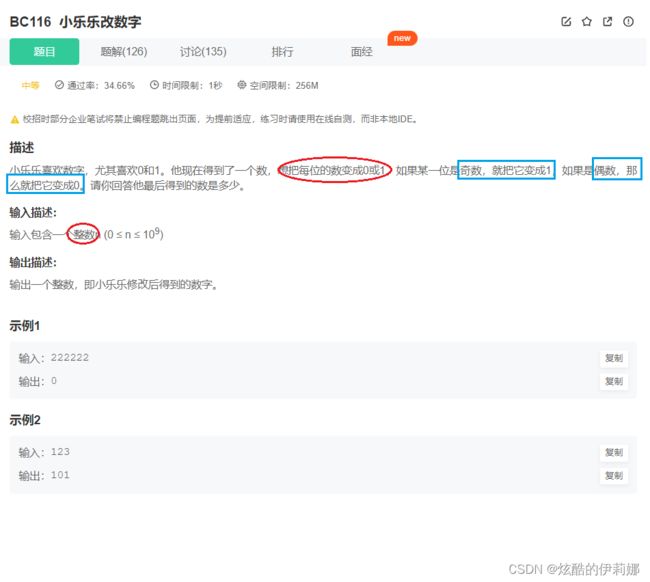
} (中等)BC116-小乐乐改数字_牛客题霸_牛客网
参考代码:
#include
#include
int main()
{
int n = 0;
int sum = 0;
scanf("%d", &n);
int i = 0;
while(n)
{
//计算每一位
int m = n%10;
//判断奇偶数
if (m % 2 == 1)
m = 1;//奇数
else
m = 0;//偶数
sum += m * pow(10, i);
n/=10;
i++;
}
printf("%d", sum);
return 0;
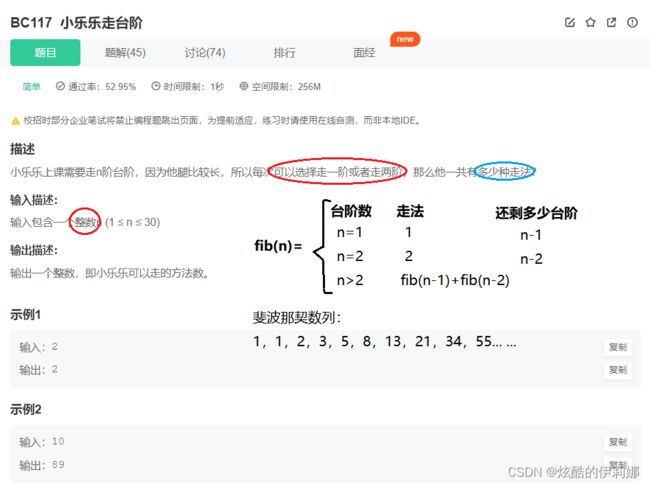
} (简单)BC117-小乐乐走台阶_牛客题霸_牛客网
解析:
- 如果只有1级台阶,那显然只有一种跳法。
- 如果有2级台阶,那么就有2种跳法,一种是分2次跳。每次跳1级,另一种就是一次跳2级。
- 如果台阶级数大于2,设为n的话,这时我们把 n 级台阶时的跳法看成n的函数,记为 f(n),第一次跳的时候有2种不同的选择:一是第一次跳一级,此时跳法的数目等于后面剩下的 n-1 级台阶的跳法数目,即为 f(n-1),二是第一次跳二级,此时跳法的数目等于后面剩下的 n-2 级台阶的跳法数目,即为 f(n-2),因此 n 级台阶的不同跳法的总数为 f(n) = f(n-1) + f(n-2),不难看出就是斐波那契数列。
参考代码:
#include
int fib(int n)
{
if(n<=2)
return n;
else
return fib(n-1)+fib(n-2);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("%d\n", ret);
return 0;
} 拓展:
【剑指Offer】算法题-青蛙跳台阶的问题
题目:一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法?
答题思路(与上面解析相同)
注意:这里需要注意一下溢出的问题,因为在 swift 里若相加溢出,则会直接crash,所以这里相加使用了 &+,溢出后返回nil。
func fibonacci(number: UInt64) -> UInt64? {
if number == 1 {
return 1
}else if number == 2 {
return 1
}
var fibNMinusOne:UInt64 = 1
var fibNMinusTwo:UInt64 = 1
var fibN:UInt64 = 0
for _ in 3...number {
fibN = fibNMinusOne &+ fibNMinusTwo
if(fibN < fibNMinusOne) {
return nil
}
fibNMinusTwo = fibNMinusOne
fibNMinusOne = fibN
}
return fibN
}若把条件修改成一次可以跳一级,也可以跳2级...也可以跳上n级呢?
思路
- 如果台阶级数为 n 的话,这时我们把 n 级台阶时的跳法看成 n 的函数,记为 f(n),第一次跳的时候有 n 种不同的选择:若是第一次跳一级,此时跳法的数目等于后面剩下的 n-1 级台阶的跳法数目,即为 f(n-1),若是第一次跳 m(m
- 因此 f(n-1)=f(n-2)+...+f(n-m)+...+f(2)+f(1)+1
- 两式相减得到 f(n)=2*f(n-1)
- 因此可以得到下面的结果
f(n)=f(n-1)+f(n-2)+...+f(n-m)+...+f(2)+f(1)+1
=1+f(1)+f(2)+...+f(n-m)+...+f(n-2)+f(n-1)
=1+f(1)+2*f(1)+...+2^(n-m-1) * f(1)+...2^(n-3) *f(1)+2^(n-2) *f(1)
=1+1+2+...+2^(n-m-1)+...2^(n-3)+2^(n-2)
=2^(n-1)
答案:
若把条件修改成一次可以跳一级,也可以跳2级...也可以跳上n级呢,则 f(n)=2^(n-1)
(参考:剑指Offer算法题-青蛙跳台阶的问题 - 简书)
(简单)BC118-小乐乐与序列_牛客题霸_牛客网
参考代码:
#include
int main()
{
int n = 0;
int arr[100001] = {0};
int i = 0;
int tmp = 0;
scanf("%d", &n);
for(i=0; i (中等) BC119- 小乐乐与字符串_牛客题霸_牛客网
解析:
- 这道题中的子串可以是不连续的。
- ch 的个数其实和前面出现的 c 的个数有关,chn 的个数和 n 之前 ch 的个数有关。
参考代码:
#include
//这个题找到的不只是连续的子串
//只要在字符串中找到几个字符能组合成子串就算是“子串”
int main()
{
char str[8000] = {0};
int count = 0;
scanf("%s", str);
//统计字符串CHN的个数
char * p = str;
long long c = 0;
long long ch = 0;
long long chn = 0;
while(*p)
{
if(*p == 'C')
c++;
else if(*p == 'H')
ch+=c;
else if(*p == 'N')
chn += ch;
p++;
}
printf("%lld\n", chn);
return 0;
} (入门)BC123-小乐乐找最大数_牛客题霸_牛客网
参考代码:
#include
int main()
{
int arr[4] = {0};
int i = 0;
for(i=0; i<4; i++)
{
scanf("%d", &arr[i]);
}
//假设arr[0]是最大值
int max = arr[0];
for(i=1; i<4; i++)
{
if(arr[i]> max)
{
max = arr[i];
}
}
printf("%d\n", max);
return 0;
} (入门)BC125-小乐乐转换成绩_牛客题霸_牛客网
参考代码:
#include
int main()
{
int score = 0;
scanf("%d", &score);
if(score >= 90 && score<=100)
printf("A\n");
else if(score >= 80 && score <= 89)
printf("B\n");
else if(score >= 70 && score <=79)
printf("C\n");
else if(score >= 60 && score <= 69)
printf("D\n");
else if(score >= 0 && score <= 59)
printf("E\n");
else
printf("F\n");
return 0;
} (简单)BC129-小乐乐计算函数_牛客题霸_牛客网
参考代码:
//代码一
#include
int max3(int a, int b, int c)
{
int max = a;
if(b>max)
max = b;
if(c>max)
max = c;
return max;
}
int main()
{
int a = 0;
int b = 0;
int c = 0;
scanf("%d %d %d", &a, &b, &c);
float m = ((float)max3(a+b,b,c)/(max3(a,b+c,c)+max3(a,b,b+c)));
printf("%.2f\n", m);
return 0;
} //代码二
#include
int max3(int a, int b, int c)
{
int max = a>b ? a:b;
max = max>c ? max:c;
return max;
}
int main()
{
int a = 0;
int b = 0;
int c = 0;
scanf("%d %d %d", &a, &b, &c);
float m = ((float)max3(a+b,b,c)/(max3(a,b+c,c)+max3(a,b,b+c)));
printf("%.2f\n", m);
return 0;
}