【贪心算法】leetcode刷题

贪心算法无固定套路。
核心思想：先找局部最优，再扩展到全局最优。

455.分发饼干

两种思路：
1、从大到小。局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。先遍历的胃口，在遍历的饼干

class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        g = sorted(g,reverse=True)
        s = sorted(s,reverse=True)
        count = 0
        si = 0
        for gi in g:
            if si<len(s) and s[si]>=gi:   # 饼干要大于胃的容量，才能喂饱
                count+=1
                si+=1             
        return count

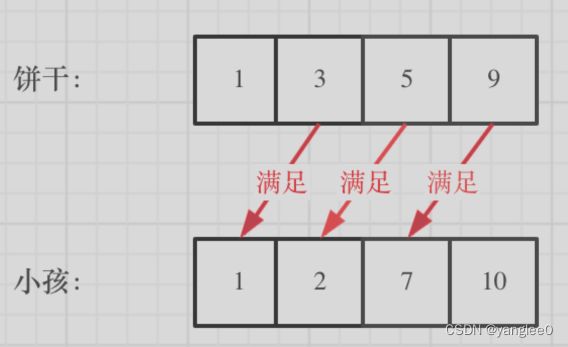
2、从小到大。小饼干先喂饱小胃口。两个循环的顺序改变了，先遍历的饼干，在遍历的胃口，这是因为遍历顺序变了，我们是从小到大遍历。

class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        g = sorted(g)
        s = sorted(s)
        count = 0
        gi = 0
        for si in s:
            if gi<len(g) and g[gi]<=si:  # 胃的容量要小于等于饼干大小才能喂饱
                count+=1
                gi+=1    
                
        return count

376. 摆动序列

具体实例：

局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。
**整体最优：**整个序列有最多的局部峰值，从而达到最长摆动序列。

考虑几种情况：

• 情况一：上下坡中有平坡
• 情况二：数组首尾两端
• 情况三：单调坡中有平坡

情况一：上下坡中有平坡

它的摇摆序列长度是多少呢？ 其实是长度是 3，也就是我们在删除的时候 要不删除左面的三个 2，要不就删除右边的三个 2。

在图中，当 i 指向第一个 2 的时候，prediff > 0 && curdiff = 0 ，当 i 指向最后一个 2 的时候 prediff = 0 && curdiff < 0。
如果我们采用，删左面三个 2 的规则，那么 当 prediff = 0 && curdiff < 0 也要记录一个峰值，因为他是把之前相同的元素都删掉留下的峰值。
所以我们记录峰值的条件应该是： (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)，为什么这里允许 prediff == 0 ，就是为了 上面我说的这种情况。

情况二：数组首尾两端
例如序列[2,5]，如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。
因为我们在计算 prediff（nums[i] - nums[i-1]） 和 curdiff（nums[i+1] - nums[i]）的时候，至少需要三个数字才能计算，而数组只有两个数字。
这里我们可以写死，就是 如果只有两个元素，且元素不同，那么结果为 2。

情况三：单调坡度有平坡

class Solution:
    def wiggleMaxLength(self, nums: List[int]) -> int:
        count = 1
        # 情况二，小于等于2的情况，可以写死
        if len(nums)<2:
            return len(nums)
        if len(nums)==2:
            if nums[-1]-nums[0]==0:
                return 1
            return len(nums)
        # 情况一以及情况三：
        prediff = 0
        for i in range(0,len(nums)-1):
            # if i>0:
            #     prediff = nums[i-1]-nums[i]
            curdiff = nums[i]-nums[i+1]
            if (prediff<=0 and curdiff>0) or (prediff>=0 and curdiff<0):
                count+=1
                prediff = curdiff   # 更新prediff
        return count  

122.买卖股票的最佳时机 II

如果想到其实最终利润是可以分解的，那么本题就很容易了！
如何分解呢？
假如第 0 天买入，第 3 天卖出，那么利润为：prices[3] - prices[0]。
相当于==(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])==。
此时就是把利润分解为每天为单位的维度，而不是从 0 天到第 3 天整体去考虑！
那么根据 prices 可以得到每天的利润序列：(prices[i] - prices[i - 1])…(prices[1] - prices[0])。

• 局部最优：收集每天的正利润，全局最优：求得最大利润。
  

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        dp = [0]*(n-1)
        for i in range(1,n):
            dp[i-1] = prices[i]-prices[i-1]
        res = 0
        for i in dp:
            if i>0:
                res+=i
        return res

55. 跳跃游戏

每次移动取最大跳跃步数（得到最大的覆盖范围），每移动一个单位，就更新最大覆盖范围。
贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点。
i 每次移动只能在 cover 的范围内移动，每移动一个元素，cover 得到该元素数值（新的覆盖范围）的补充，让 i 继续移动下去。
而 cover 每次只取 max(该元素数值补充后的范围, cover 本身范围)。
如果 cover 大于等于了终点下标，直接 return true 就可以了。

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        n = len(nums)
        cover = 0
        if n<2:
            return True
        for i in range(n-1):
            if cover>=i:
                cover = max(cover,i+nums[i])
            if cover>=n-1:
                return True
        return False

45.跳跃游戏 II

如果移动下标等于当前覆盖最大距离下标， 需要再走一步（即 ans++），因为最后一步一定是可以到的终点。（题目假设总是可以到达数组的最后一个位置），如图：

如果移动下标不等于当前覆盖最大距离下标，说明当前覆盖最远距离就可以直接达到终点了，不需要再走一步。如图：

class Solution:
    def jump(self, nums: List[int]) -> int:
		cur_distance = 0  # 当前覆盖的最远距离下标
        ans = 0  # 记录走的最大步数
        next_distance = 0  # 下一步覆盖的最远距离下标
        
        for i in range(len(nums) - 1):  # 注意这里是小于len(nums) - 1，这是关键所在
            next_distance = max(nums[i] + i, next_distance)  # 更新下一步覆盖的最远距离下标
            if i == cur_distance:  # 遇到当前覆盖的最远距离下标
                cur_distance = next_distance  # 更新当前覆盖的最远距离下标
                ans += 1
        
        return ans

1005.K次取反后最大化的数组和

class Solution:
    def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:
        nums.sort(key=lambda x:abs(x),reverse=True)  # 按照绝对值的个数排序,且从大到小，为了后面先将前k个大负数进行翻转为正数，保证和最大
        for i in range(len(nums)):
            if nums[i]<0 and k>0:   # 将负数都翻转为正数
                k-=1
                nums[i] = -nums[i]
                
        # 现在全部都是正数了
        if k%2==1: # 如果还剩奇数个，则将最小的正数翻转
            nums[-1] = -nums[-1]

        # 如果是偶数，其实不用管，因为随便翻转个正数偶数次就可以了，不影响最后结果
        return sum(nums)

134. 加油站

分发糖果

• 从左到右：
  如果ratings[i] > ratings[i - 1] 那么[i]的糖 一定要比[i - 1]的糖多一个，所以贪心：candyVec[i] = candyVec[i - 1] + 1
  
• 从右到左考虑：
  再确定左孩子大于右孩子的情况（从后向前遍历）
  遍历顺序这里有同学可能会有疑问，为什么不能从前向后遍历呢？
  因为 rating[5]与rating[4]的比较 要利用上 rating[5]与rating[6]的比较结果，所以 要从后向前遍历。
  如果从前向后遍历，rating[5]与rating[4]的比较 就不能用上 rating[5]与rating[6]的比较结果了 。如图：
  

如果 ratings[i] > ratings[i + 1]，此时candyVec[i]（第i个小孩的糖果数量）就有两个选择了，一个是candyVec[i + 1] + 1（从右边这个加1得到的糖果数量），一个是candyVec[i]（之前比较右孩子大于左孩子得到的糖果数量）。
那么又要贪心了，局部最优：取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，保证第i个小孩的糖果数量既大于左边的也大于右边的。全局最优：相邻的孩子中，评分高的孩子获得更多的糖果。

所以就取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多，也比右边candyVec[i + 1]的糖果多。

class Solution:
    def candy(self, ratings: List[int]) -> int:
        k = len(ratings)
        dp = [1]*k
        # 从左到右
        for i in range(k):
            if i>0 and ratings[i]>ratings[i-1]:
                dp[i] = dp[i-1]+1
        # 从右到左
        for i in range(k-2,-1,-1):
            if ratings[i]>ratings[i+1]:
                dp[i] = max(dp[i+1]+1,dp[i])  # 关键点 见解析
        return sum(dp)