动态规划总结
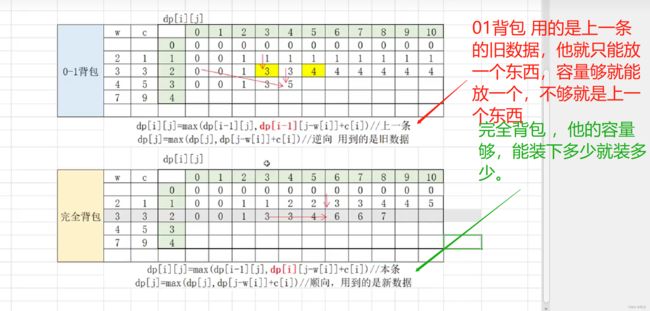
1,01背包dp(每件物品最多选一次):
因为背包为0 的时候,什么都装不了,所以为零 ,就是他们的最优解。
最后一个单元格为最后的答案。
01背包模板
public class Knapsack {
public static int knapsack(int[] weights, int[] values, int capacity) {
int n = weights.length;
int[][] dp = new int[n + 1][capacity + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= capacity; j++) {
if (weights[i - 1] > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1]);
}
}
}
return dp[n][capacity];
}
public static void main(String[] args) {
int[] weights = {10, 20, 30};
int[] values = {60, 100, 120};
int capacity = 50;
System.out.println("The maximum value that can be put in a knapsack of capacity " + capacity + " is: "
+ knapsack(weights, values, capacity));
}
}当j比现在取的物品重量小的时候:
继承上一个的值:——>dp[i][j] = dp[i - 1][j](上一个物品价值);
当j>=w[i]:有两种情况,一种是拿,一种是不拿:
核心: dp[i][j] = Math.max(dp[i - 1][j](不拿), dp[i - 1][j - weights[i - 1]] + values[i - 1](拿));
难点: 这里表示,如果容量为3 ,之前存放的一直是重量2 的价值 , 那么遇到一个重量为3 的价值更高的, 那么我们肯定选择更高的 那么要就要更新重量为2 的价值为重量3的价值 ,dp[i - 1][j - weights[i - 1]] + values[i - 1](价值);
在以上代码中,我们定义了一个函数 knapsack 接受三个参数:weights表示物品的重量数组,values表示物品的价值数组,capacity表示背包的容量。我们首先初始化一个大小为(n+1)x(capacity+1)的二维数组dp。其中,dp[i][j]表示前i个物品放入容量为j的背包中所能获得的最大价值。
然后,我们使用两个嵌套的for循环来计算每个dp[i][j]的值。对于dp[i][j],如果第i个物品的重量weights[i-1]大于当前背包容量j,则表示第i个物品无法放入背包中,只能继承上一个状态dp[i-1][j]的价值。否则,我们需要比较将第i个物品放入背包时所得到的价值与不放入背包时所得到的价值哪一个更大,并更新dp[i][j]为较大者。
最后,我们返回dp[n][capacity],即为前n个物品放入容量为capacity的背包中所能获得的最大价值。在主函数中,我们提供了一个测试样例来验证代码的正确性。
以下是Java语言实现的01背包问题的模板代码,包含详细的注释解释每一步的实现过程:```java
public class Knapsack {
/**
* 01背包问题
* @param weight 物品重量数组
* @param value 物品价值数组
* @param capacity 背包容量
* @return 最大价值
*/
public int knapsack(int[] weight, int[] value, int capacity) {
int n = weight.length; // 物品数量
// 创建一个二维数组用于存储状态转移表
int[][] dp = new int[n + 1][capacity + 1];
// 初始化状态转移表,当物品数量 i=0 或者背包容量 j=0 时,最大价值为0
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= capacity; j++) {
dp[i][j] = 0;
}
}
// 动态规划填充状态转移表
for (int i = 1; i <= n; i++) { // 遍历所有物品
for (int j = capacity; j >= weight[i - 1]; j--) { // 遍历所有容量(倒序遍历)
if (j >= weight[i - 1]) { // 当前物品可以放入背包中时,取最大价值
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
} else { // 当前物品无法放入背包中,则最优解仍然是之前的状态
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[n][capacity]; // 返回前n个物品能够装入容量为capacity的背包中所获得的最大价值
}
public static void main(String[] args) {
Knapsack knapsack = new Knapsack();
int[] weight = {2, 3, 4, 5}; // 物品重量数组
int[] value = {3, 4, 5, 6}; // 物品价值数组
int capacity = 8; // 背包容量
int max_value = knapsack.knapsack(weight, value, capacity); // 最大价值
System.out.println("最大价值:" + max_value);
}
}希望以上代码和注释能够帮助您更好地理解01背包问题的求解过程。
以下是Java的01背包问题状态压缩代码模板:
public int knapsack(int[] weight, int[] value, int capacity) {
int n = weight.length;
int[] dp = new int[capacity + 1];
for (int i = 0; i < n; i++) {
for (int j = capacity; j >= weight[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
return dp[capacity];
}逆向的
与二维数组不同,状态压缩采用了一维数组 `dp` 来存储状态,其中 `dp[j]` 表示当容量为j时所能获得的最大价值。在循环方面,我们采用了正序循环的方式,保证每次计算 `dp[j]` 时,子问题中的状态都已经被更新过。
例题1:
问题描述
给定N种砝码(每种个数不限)和一个整数M,求至少需要几个砝码才可以称出刚好M克。(n<=100,m<=1000)
[输入格式]:n,m,n个整数Wi表示砝码的质量。
[输出格式]:最少需要的砝码数或impossible表示无法满足。
样例输入
5 33
12 21 3 4 6
样例输出
2
样例说明
即12+21两个砝码可以称得33
package 算法提高;
import java.util.Arrays;
import java.util.Scanner;
public class 砝码称重 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
//输入几种砝码
int n = scanner.nextInt();
//输入目标值
int m = scanner.nextInt();
//定义dp数组
int INF = 0x7f7f7f7f;
int[] dp = new int[m + 1];
//初始化dp dp[i]表示重量为i时最少需要的砝码数
Arrays.fill(dp, INF);
dp[0]=0;//注意 0位置的是0 不要瞎弄
//每个砝码的重量
int[] w = new int[n];
for (int i = 0; i < n; i++) {
w[i] = scanner.nextInt();
}
for (int i = 0; i < n; i++) {
for (int j = w[i]; j <= m; j++) {
if (dp[j - w[i]] != INF) {
dp[j] = Math.min(dp[j], dp[j - w[i]] + 1);
}
}
}
if (dp[m] == INF) {
System.out.println("impossible");
} else {
System.out.println(dp[m]);
}
scanner.close();
}
}
问题描述:
本题的目标是求出给定N种砝码中最少需要使用多少个才能称出整数M克,其中每种砝码数量不限。
具体解决方法为使用动态规划算法,构建dp数组并通过遍历尝试各种方式计算M克质量,最后输出最少需要的砝码数或者impossible。
例题2 : Acwing 01背包
package Acwing;
import java.util.Scanner;
public class 零1背包 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), w = sc.nextInt();
int a[] = new int[n + 1];
int b[] = new int[n + 1];
for (int i = 1; i <= n; i++) {
a[i] = sc.nextInt();
b[i] = sc.nextInt();
}
int dp[][] = new int[n + 1][w + 1];
for (int i = 1; i <= n; i++) {
for (int j = 0; j <=w; j++) {
if (j < a[i]) {
dp[i][j] = dp[i - 1][j];
}else
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - a[i]] + b[i]);
}
}
System.out.println(dp[n][w]);
}
}
2,多重背包dp(每件物品选区次数有限):
public class MultipleKnapsack {
public static void main(String[] args) {
int[] w = {2, 3, 4}; // 物品的体积
int[] v = {1, 3, 5}; // 物品的价值
int[] c = {2, 3, 1}; // 物品的数量
int n = w.length; // 物品的个数
int W = 7; // 背包的容量
int[][] dp = new int[n + 1][W + 1]; // dp数组
for (int i = 1; i <= n; i++) { // 外层循环枚举每个物品
for (int j = 0; j <= W; j++) { // 内层循环枚举背包容量
for (int k = 0; k <= c[i - 1] && k * w[i - 1] <= j; k++) { // 最内层循环枚举物品数量并计算状态转移方程
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - k * w[i - 1]] + k * v[i - 1]);
}
}
}
System.out.println("在背包容量为" + W + "的情况下,能够获取到的最大价值为:" + dp[n][W]);
}
}
说明:
w数组表示物品的体积。
v数组表示物品的价值。
c数组表示物品的数量。
n表示物品的个数。
W表示背包的容量。
dp数组表示动态规划状态,其中dp[i][j]表示前i个物品放入容量为j的背包中能够获得的最大价值。
外层循环枚举每个物品,内层循环枚举容量,最内层循环枚举物品数量,并计算状态转移方程。
3,完全背包dp(每件物品可以选无限次):
public class CompleteKnapsack {
public static void main(String[] args) {
int[] w = {2, 3, 4}; // 物品的体积
int[] v = {1, 3, 5}; // 物品的价值
int n = w.length; // 物品的个数
int W = 7; // 背包的容量
int[][] dp = new int[n + 1][W + 1]; // dp数组
for (int i = 1; i <= n; i++) { // 外层循环枚举每个物品
for (int j = w[i - 1]; j <= W; j++) { // 内层循环枚举背包容量,并计算状态转移方程
dp[i][j] = Math.max(dp[i][j], dp[i][j - w[i - 1]] + v[i - 1]);
}
}
System.out.println("在背包容量为" + W + "的情况下,能够获取到的最大价值为:" + dp[n][W]);
}
}
说明:
w数组表示物品的体积。
v数组表示物品的价值。
n表示物品的个数。
W表示背包的容量。
dp数组表示动态规划状态,其中dp[i][j]表示前i个物品放入容量为j的背包中能够获得的最大价值。
外层循环枚举每个物品,内层循环枚举容量,并计算状态转移方程。由于是完全背包,所以第i个物品可以选无限次,因此状态转移方程为dp[i][j] = Math.max(dp[i][j], dp[i][j - w[i - 1]] + v[i - 1])。
下面是用Java语言写的完全背包问题的状态压缩模板:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 物品数量
int n = sc.nextInt();
// 背包容量
int m = sc.nextInt();
// 物品体积和价值数组
int[] v = new int[n + 1];
int[] w = new int[n + 1];
for (int i = 1; i <= n; i++) {
v[i] = sc.nextInt();
w[i] = sc.nextInt();
}
// dp数组,其中第i行表示前i个物品在不超过j的背包容量时可以获得的最大价值
// 因为是状态压缩,所以一维数组即可代表dp数组
int[] dp = new int[m + 1];
// 状态转移方程:dp[j]表示不超过背包容量j时可以获得的最大价值
for (int i = 1; i <= n; i++) {
for (int j = v[i]; j <= m; j++) {
dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
}
}
System.out.println(dp[m]);
}
}状态转移方程: dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
这个模板中使用了一个一维数组来存储状态。对于每个物品,我们遍历了从它自己到背包容量m之间的每个可能体积,计算出加入这个物品时可以得到的最大价值。
在这个模板中,我们并没有记录每个状态下选择了哪些物品,只记录了不同体积下可以得到的最大价值。如果需要知道具体选择了哪些物品来得到这个最大价值,可以进一步修改代码。
4,序列dp
1,LCS代码模板:
public class LCS {
public static int lcs(String str1, String str2) {
int m = str1.length();
int n = str2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
dp[i][j] = 0;
} else if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
public static void main(String[] args) {
String str1 = "AGGTAB";
String str2 = "GXTXAYB";
System.out.println("Length of LCS is: " + lcs(str1, str2));
}
}这里使用的是动态规划算法来求解LCS问题。在以上代码中,lcs函数接受两个字符串作为参数并返回它们的最长公共子序列的长度。我们首先初始化一个二维数组 dp,其中第一行和第一列都置为零。然后我们通过比较字符串中字符是否相等,来填充剩余部分的dp数组。
最后,我们返回 dp[m][n],其中 m 和 n 分别是两个字符串的长度。在主函数中,我们提供了两个字符串来测试我们的代码
2,LIS(最长上升子序列)问题的代码模板:
public class LIS {
public static int lis(int[] nums) {
int n = nums.length;
int[] dp = new int[n];
Arrays.fill(dp, 1);
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
int maxLen = 0;
for (int len : dp) {
maxLen = Math.max(maxLen, len);
}
return maxLen;
}
public static void main(String[] args) {
int[] nums = {10, 9, 2, 5, 3, 7, 101, 18};
System.out.println("The length of the longest increasing subsequence is: " + lis(nums));
}
}
在以上代码中,我们定义了一个函数 lis 接受一个整数数组作为参数,并返回该数组的最长上升子序列的长度。我们首先初始化一个大小为n的数组dp,其中dp[i]表示以数字nums[i]结尾的最长上升子序列长度。
然后,我们使用两个嵌套for循环来计算每个dp[i]的值。对于dp[i],我们比较它与前面各个数nums[j]是否存在递增关系,如果存在,则更新dp[i]=dp[j]+1。
最后,我们遍历所有dp[i]并返回其中的最大值,即为最长上升子序列的长度。在主函数中,我们提供了一个整数数组来测试我们的代码。
3,最大子序列和问题
最大子序列和问题是指在一个给定序列中,找到一个连续的子序列,使得该子序列的元素和最大。常见的解法有暴力枚举、分治算法和动态规划等。
下面是使用动态规划解决最大子序列和问题的模板,时间复杂度为 O(n):
public int maxSubArray(int[] nums) {
int n = nums.length;
int[] dp = new int[n];
dp[0] = nums[0];
int res = dp[0];
for (int i = 1; i < n; ++i) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
// dp[i]= Math.max(dp[i-1],dp[i])+num[i];(也可以)
res = Math.max(res, dp[i]);
}
return res;
}其中 dp 数组表示以第 i 个元素结尾的最大子序列和,状态转移方程为:
dp[i] = max(dp[i-1]+nums[i] , nums[i] )
dp[i]= Math.max(dp[i-1],dp[i])+num[i];(也可以)
即如果前面累加和为正数,则加上当前元素可以使得结果更大;如果前面累加和为负数,则以当前元素作为起点可以使得结果更大。在遍历过程中不断更新 res 取得全局最优解。
例如,在数组 [−2,1,−3,4,−1,2,1,−5,4] 中,以第 i 个元素结尾的最大子序列如下所示:
i=0: -2
i=1: 1
i=2: -2
i=3: 4
i=4: 3
i=5: 5
i=6: 6
i=7: 1
i=8: 5通过比较这些最大子序列和的大小,可得到该数组的最大子序列和为 6+1+(-2)+4 = 9。
希望对你有所帮助!
5,计数dp
以下是Java计数dp的模板:
public class CountingDP {
public static void main(String[] args) {
int n = 10; // 数字范围为1到n
int target = 30; // 目标数字
int[] nums = {2, 3, 5}; // 可选择的数字数组
int[] dp = new int[target + 1]; // dp数组
dp[0] = 1;
for (int i = 0; i < nums.length; i++) { // 外层循环枚举可选择的数字
for (int j = nums[i]; j <= target; j++) { // 内层循环枚举目标数字,并计算状态转移方程
dp[j] += dp[j - nums[i]];
}
}
System.out.println("在" + n + "以内,由" + Arrays.toString(nums) + "组成的和为" + target + "的序列个数为:" + dp[target]);
}
}
说明:
n表示数字范围为1到n。
target表示目标数字。
nums表示可选择的数字数组。
dp数组表示动态规划状态,其中dp[i]表示由给定的可选数字组成和为i的序列个数。
外层循环枚举可选择的数字,内层循环枚举目标数字,并计算状态转移方程。由于可以重复使用数字,因此状态转移方程为dp[j] += dp[j - nums[i]]。最终dp[target]即为由给定的可选数字组成和为目标数字的序列个数。
6,状态压缩dp
状态压缩dp是一种优化dp的算法,它主要是通过压缩状态来减小动态规划的状态空间,从而降低时间复杂度。Java中实现状态压缩dp也很简单,下面是一份模板代码:
// 状态压缩dp模板
public static int stateCompressDP(int[][] cost) {
int n = cost.length;
int m = 1 << n; // 状态数
int[] dp = new int[m];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
for (int s = 0; s < m; s++) {
for (int i = 0; i < n; i++) {
if ((s & (1 << i)) == 0) { // 当前状态未访问过i节点
for (int j = 0; j < n; j++) {
if ((s & (1 << j)) != 0) { // 当前状态已经被访问过j节点
dp[s | (1 << i)] = Math.min(dp[s | (1 << i)], dp[s] + cost[j][i]);
}
}
}
}
}
return dp[m - 1];
}
这份代码主要是求解一个图中所有节点之间的最短距离,其中cost[i][j]表示第i个节点到第j个节点的距离。在代码中,我们先计算出状态总数m(即2^n),然后用一个一维数组dp来存储状态对应的最短距离。在状态转移时,我们遍历所有节点,如果当前状态未访问过i节点,且已经访问过j节点,则更新dp数组。
注意,在Java中我们可以使用位运算符来实现状态压缩dp的计算。例如,“(s & (1 << i))”表示将数字s的第i位取出来进行运算。此外,我们还需要预先给dp数组赋值一个最大值(例如Integer.MAX_VALUE),以便在初始化时区分已经计算完成的结果与未计算完成的结果。
希望这份代码能够帮助到你!
7,数位dp
Java数位dp模板是一种用于解决数位相关问题的算法模板,通常用于计算一个数的各个数位上数字之和、寻找一个区间内满足某些条件的数的个数等问题。
以下是Java数位dp模板的代码:
public static int dfs(int pos, int sum, int limit) {
if (pos == -1) return sum; // 边界条件
if (!limit && dp[pos][sum] != -1) return dp[pos][sum]; // 记忆化搜索
int maxDigit = limit ? digits[pos] : 9; // 限制最大值
int res = 0;
for (int i = 0; i <= maxDigit; i++) {
res += dfs(pos - 1, sum + i, limit && i == maxDigit);
}
if (!limit) dp[pos][sum] = res; // 记录状态,避免重复计算
return res;
}
其中,pos表示当前处理的数位,sum表示当前已经累加的数字和,limit表示是否达到了最大值。接下来对每一行具体进行解释。
首先判断是否到达了边界条件 pos == -1 ,如果到达则返回累加后的结果。
其次判断是否需要进行记忆化搜索。当 limit 为 false 并且 dp[pos][sum] 不等于 -1,则说明已经计算过该状态,并将其保存在 DP 数组中。如果存在该状态,则直接返回该状态对应的值。
然后,我们需要计算当前位置可以取到的最大数字。当 limit 为 true 时,我们只能取到该位置上的数字。当 limit 为 false 时,我们可以取到0~9之间的所有数字。
接下来使用for循环枚举下一位可以取到的所有数字,并进行递归调用。这里需要注意一下 limit && i == maxDigit 这个条件,它表示如果当前位置取到的数字等于上限,那么下一位只能取更小的数字。
最后,如果 limit 为 false,则我们将计算结果 res 保存在 DP 数组中,避免重复计算。而如果 limit 为 true,则不需要记录结果,因为每次都需要重新计算。
总而言之,Java数位dp模板是一个常用的处理数位相关问题的算法模板。它可以避免递归层数过多、数据规模太大而导致的爆栈或超时等问题。
8,区间dp
for (int len = 2; len <= n; len++) { // 枚举区间长度
for (int i = 1; i + len - 1 <= n; i++) { // 枚举左端点
int j = i + len - 1; // 计算右端点
for (int k = i; k < j; k++) { // 枚举分割点
dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[k+1][j] + calc(i, j)); // 转移方程
}
}
}
其中,n表示序列的长度,i和j表示当前枚举的区间起始点和终止点,k表示当前枚举的分割点。接下来对每一行具体进行解释。
首先枚举区间长度 len ,从2开始到n为止。这里需要注意,当 len=1 时,该子问题已经被计算过了,直接跳过即可。
然后枚举左端点 i ,注意循环终止条件应为 (i + len - 1) <= n ,以保证子问题不越界。
接下来计算右端点 j ,直接令 j = i + len - 1 即可。
接着枚举分割点 k ,注意循环终止条件应为 k < j ,以保证分割点在区间内部。
然后根据题目要求构造转移方程,通常形如:dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[k+1][j] + calc(i, j)) 。这里需要注意一下计算的顺序,首先需要计算出子区间的DP值,然后再结合当前分割点计算出整个区间的DP值。
最后得到的是区间 [1,n] 的最优解,也可以根据题目需求更改其它左右端点的结果。
总而言之,Java区间dp模板是一个常用的解决区间问题的算法模板。除了以上代码框架外,每道具体题目还需要针对其特殊性质作相应修改。