6.4.3 1x1卷积层
特点:1x1卷积层相当于全连接层
作用:1x1卷积用于调整网络层的通道数量和控制模型复杂度
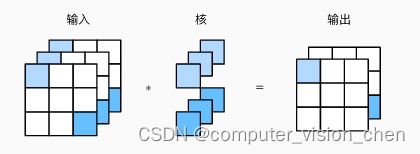 输入形状:(通道,行,列) = (3,3,3)
输入形状:(通道,行,列) = (3,3,3)
卷积核形状:(输出通道,输入通道,行,列) = (2,3,1,1)
输出形状:(通道,行,列) = (2,3,3)
import cv2
import torch
from torch import nn
from d2l import torch as d2l
一.使用神经网络全连接的方式实现对X使用1x1卷积
def corr2d_multi_in_out_1x1(X,K):
c_i,h,w = X.shape
c_o = K.shape[0]
X = X.reshape((c_i,h*w))
K = K.reshape((c_o,c_i))
Y = torch.matmul(K,X)
# 全连接层中的矩阵乘法
return Y.reshape((c_o,h,w))
二.使用卷积函数计算 对X使用1x1卷积
def corr2d_multi_in(X,K):
return sum(d2l.corr2d(x,k) for x,k in zip(X,K))
'''多输入和多输出通道'''
def corr2d_multi_in_out(X,K):
# 注意,没有遍历X,此时的X是大写
return torch.stack([corr2d_multi_in(X,k) for k in K],0)
# 生成均值为0,方差为1的 3通道的3x3矩阵
X = torch.normal(0,1,(3,3,3))
# 生成均值为0,方差为1的 输出通道为2,输入通道为3,3x3矩阵
K = torch.normal(0,1,(2,3,1,1))
Y1 = corr2d_multi_in_out_1x1(X,K)
Y2 = corr2d_multi_in_out(X,K)
# Y1结果
tensor([[[-0.3174, -0.3736, -0.3822],
[-1.2920, -0.7917, -1.0706],
[ 2.1018, -1.1783, 0.7724]],
[[-0.4680, 3.2644, 1.2653],
[ 2.7322, -0.4164, -0.0810],
[-2.7743, 2.0169, -1.3969]]])
# Y2结果
tensor([[[-0.3174, -0.3736, -0.3822],
[-1.2920, -0.7917, -1.0706],
[ 2.1018, -1.1783, 0.7724]],
[[-0.4680, 3.2644, 1.2653],
[ 2.7322, -0.4164, -0.0810],
[-2.7743, 2.0169, -1.3969]]])
# 当Y1与Y2的差<1e-6时继续执行,否则报错。
assert float(torch.abs(Y1-Y2).sum()) < 1e-6
补充 assert函数
一、assert函数
断言函数
二、assert 表达式:
当表达式为真时,程序继续往下执行,只是判断,不做任何处理;
当表达式为假时,抛出AssertionError错误,并将 [参数] 输出
三、用法
1、assert语句用来声明某个条件是真的。
2、如果你非常确信某个你使用的列表中至少有一个元素,而你想要检验这一点,并且在它非真的时候引发一个错误,那么assert语句是应用在这种情形下的理想语句。
3、当assert语句失败的时候,会引发一AssertionError。