PID知识总结

PID算法算是控制系统中一个比较常见的控制算法了，特别是在闭环控制系统中，PID的使用尤为常见，鄙人由于电赛延期在家闲来无事，决定把自己在电赛备赛期间所学的PID知识总结一下，希望自己在总结的时候能“温故而知新”，同时也请各位大佬能有所指正，揪出我的错误。

1.PID的算法简介

PID即：Proportional（比例）、Integral（积分）、Differential（微分）的缩写。顾名思义，PID控制算法是结合比例、积分和微分三种环节于一体的控制算法，PID控制的实质就是根据输入的偏差值，按照比例、积分、微分的函数关系进行运算，运算结果用以控制输出。
简单的概括为一句话：PID算法将所求误差的比例，积分，微分进行线性组合组成控制量，将控制量对控制变量进行控制的算法。

PID的数学公式

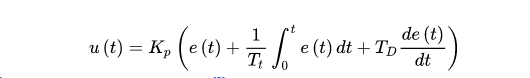
式中，Kp——比例增益，Kp与比例度成倒数关系；
Tt——积分时间常数；
TD——微分时间常数；
u（t）——PID控制器的输出信号；
e（t）——给定值r（t）与测量值之差。

闭环控制的PID的控制流程图

PID算法中常见的有两种：

1.位置式PID控制算法
2.增量式PID控制算法

两者算法有什么区别：
1增量式算法不需要做累加，控制量增量的确定仅与最近几次偏差采样值有关，计算误差对控制 量计算的影响较小。而位置式算法要用到过去偏差的累加值，容易产生较大的累加误差。

2增量式算法得出的是控制量的增量，例如在阀门控制中，只输出阀门开度的变化部分，误动作 影响小，必要时还可通过逻辑判断限制或禁止本次输出，不会严重影响系统的工作。 而位置式的输出直接对应对象的输出，因此对系统影响较大。

3增量式PID控制输出的是控制量增量，并无积分作用，因此该方法适用于执行机构带积分部件的对象，如步进电机等，而位置式PID适用于执行机构不带积分部件的对象，如电液伺服阀。

1.1增量式PID

因为我们是单片机对数据进行采集，对数据进行离散采取，所以我们使用的是离散式增量式PID
数学公式如下：

算法如下（增量式PI控制速度）

/**************************************************************************
函数功能：速度闭环PID控制(实际为PI控制)
入口参数：目标速度 当前速度
返回  值：速度控制值
根据增量式离散PID公式 
ControlVelocity+=Kp[e（k）-e(k-1)]+Ki*e(k)+Kd[e(k)-2e(k-1)+e(k-2)]
e(k)代表本次偏差 
e(k-1)代表上一次的偏差  以此类推 
ControlVelocity代表增量输出
在我们的速度控制闭环系统里面，只使用PI控制
ControlVelocity+=Kp[e（k）-e(k-1)]+Ki*e(k)
**************************************************************************/
int Velocity_FeedbackControl(int TargetVelocity, int CurrentVelocity) 
{
		int Bias;  //定义相关变量
		static int ControlVelocity, Last_bias; //静态变量，函数调用结束后其值依然存在
		
		Bias=TargetVelocity-CurrentVelocity; //求速度偏差
		
		ControlVelocity+=Velcity_Kp*(Bias-Last_bias)+Velcity_Ki*Bias;  //增量式PI控制器
                                                                   //Velcity_Kp*(Bias-Last_bias) 作用为限制加速度
	                                                                 //Velcity_Ki*Bias             速度控制值由Bias不断积分得到 偏差越大加速度越大
		Last_bias=Bias;	
		return ControlVelocity; //返回速度控制值
}

在我使用增量式PID中，我大多使用的是增量式PI对霍尔电机进行速度控制。

1.2位置式PID

同样原理，所以我们使用的是离散式位置式PID
数学公式如下：

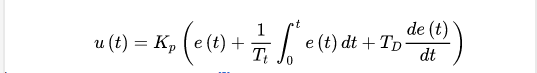
算法如下

/**************************************************************************
函数功能：位置式PID控制器
入口参数：目标圈数(位置) 当前位置
返回  值：速度控制值
根据位置式离散PID公式 
pwm=Kp*e(k)+Ki*∑e(k)+Kd[e（k）-e(k-1)]
e(k)代表本次偏差 
e(k-1)代表上一次的偏差  
∑e(k)代表e(k)以及之前的偏差的累积和;其中k为1,2,,k;
pwm代表输出
**************************************************************************/
int Position_FeedbackControl(float Circle, int CurrentPosition)
{
		float TargetPosition,Bias, ControlVelocity;     //定义相关变量
		static float Last_bias, Integral_Bias;          //静态变量，函数调用结束后其值依然存在

		Bias=TargetPosition-CurrentPosition; //求位置偏差
	  Integral_Bias+=Bias;
    if(Integral_Bias> 970) Integral_Bias= 970;	//积分限幅 防止到达目标位置后过冲，这里的值可以自由修改，我在这里修改为970
	  if(Integral_Bias<-970) Integral_Bias=-970;	//积分限幅 防止到达目标位置后过冲
	
		ControlVelocity=Position_Kp*Bias+Position_Ki*Integral_Bias+Position_Kd*(Bias-Last_bias);  //位置式PI控制器
	                                                                                            //Position_Kp*Bias 偏差越大速度越大
	                                                                                            //Position_Ki*Integral_Bias 减小稳态误差
	                                                                                            //Position_Kd*(Bias-Last_bias) 限制速度

		Last_bias=Bias;	   //更新误差
		return ControlVelocity;    //返回速度控制值 
}

在这里我是通过位置式PID对电机进行控制，控制电机旋转至目标位置

注意:
1：位置式PID不是专门用来控制目标进行目标位置的移动，位置式PID也可以用来控制速度，位置式PID中的位置并非电机的位置，这里的位置是指PID计算结果与信号的对应关系

2：位置式PID在积分项达到饱和时,误差仍然会在积分作用下继续累积，一旦误差开始反向变化，系统需要一定时间从饱和区退出，所以在u(k)达到最大和最小时，要停止积分作用，并且要有积分限幅

2.串级PID

在这里我推荐大家看这位博主对串级PID的解析，我对串级PID的理解也是通过他的博客才有所加深
串级PID的理解

串级PID的定义：

串级控制系统是改善控制质量的有效方法之一，在过程控制中得到了广泛的应用。所谓串级控制，就是采用两个控制器串联工作，外环控制器的输出作为内环控制器的设定值，由内环控制器的输出去操纵控制阀，从而对外环被控量具有更好的控制效果。这样的控制系统被称为串级系统。PID串级控制就是串级控制中的两个控制器均为PID控制器。

其流程图如下：

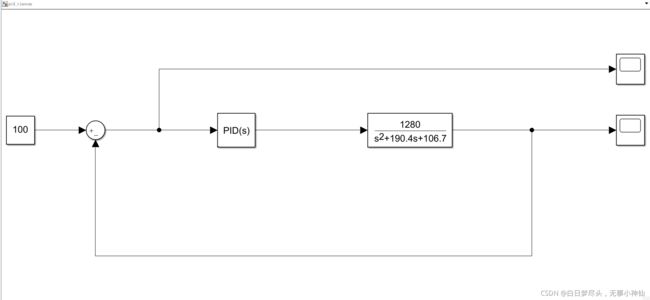
上图就是平衡小车的串级PID的流程图，

在上面的流程图中：先是在角度环PID中计算角度误差，通过角度环PID输出期望角速度，再通过角速度PID控制速度达到期望速度，在通过角速度PID输出角度反馈进行角度环PID。

其特点就是角度环PID的输出就是角速度PID的输入，角速度PID的输出就是角度环PID的输入，各个PID相互影响。

我可能写的不是非常好，大家可以查找一下一些相关博主的资料，他们相应的串级PID文章写的非常好，易于理解。

3.PID的调参

其实PID最难的部分就是PID的调参了，可以说PID的调参是整个PID的学习核心，那么PID怎么进行调参呢？
在这里我主要介绍一下这两种的调参方式：matlab调参和经验调参，这两种方式比较常见而且实际调参比较多。

3.1matlab调参

在讲matlab调参之前，我先介绍一本书

在这本书里介绍了matlab怎么对PID进行仿真，调参和实际应用。我感觉这本书讲的非常好，大家可以看看，对PID和matlab的应用有很大的理解。

在进行调参之前，我们先要用simulink对PID进行仿真，构建一个仿真图。在这里我先构建一个PID仿真图（simulink怎么进行PID仿真我先不介绍了，到时候我会另写博客进行细讲）

这里我们是预先知道相应的传递函数，如果不知道相应的传递函数，我们可以用matlab的系统传递进行求解，在这里我就不细说了，我会写另一个博客怎么对系统传递进行传递函数的使用。

在写出仿真图后我们进行PID的自动调参
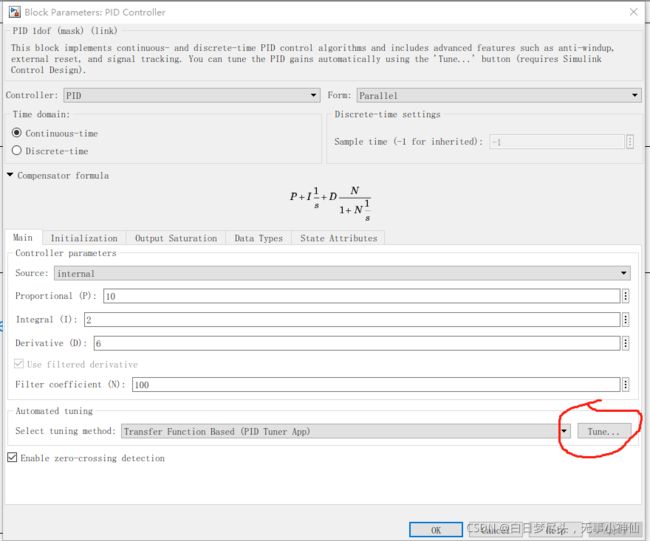
在Domain那里选择时间，在中间的Response Time 和 Transient 那里移动滑轮，直至曲线平滑（中间的曲线是matlab自动调参的曲线，可根据自己的要求进行相应的更改，实线是我们目前的matlab的曲线）

3.2经验调参

经验调参其实主要靠自己平时的调参经验所得到的，这有时要看玄学的，我刚开始也不信这经验调参的，但是他有事往往出效果了。
在经验调参这里我是基于这个口诀的：
参数整定找最佳， 从小到大顺序查。
先是比例后积分， 最后再把微分加。
曲线振荡很频繁， 比例度盘要放大。
曲线漂浮绕大弯， 比例度盘往小扳。
曲线偏离回复慢， 积分时间往下降。
曲线波动周期长， 积分时间再加长。
曲线振荡频率快， 先把微分降下来。
动差大来波动慢， 微分时间应加长。
理想曲线两个波， 前高后低四比一。
一看二调多分析， 调节质量不会低。

不过在调参之前，我会分析PID的极性，先判断PID的极性在进行口诀进行参数调节