5_普通最小二乘法线性回归案例（Scikit-learn 0.18.2）

• 现有一批描述家庭用电情况的数据，对数据进行算法模型预测，并最终得到预测模型（每天各个时间段和功率之间的关系、功率与电流之间的关系等）

  • 数据来源：Individual household electric power consumption Data Set
  • 建议：使用python的sklearn库的linear model中LinearRegression来获取算法
  • 开发环境：https://scikit-learn.org/0.18/

# 引入所需要的全部包
from sklearn.model_selection import train_test_split # 数据划分的类
from sklearn.linear_model import LinearRegression # 线性回归的类
from sklearn.preprocessing import StandardScaler # 数据标准化

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
from pandas import DataFrame
import time

## 设置字符集，防止中文乱码
mpl.rcParams['font.sans-serif']=[u'simHei']
mpl.rcParams['axes.unicode_minus']=False

# 加载数据
# 日期、时间、有功功率、无功功率、电压、电流、厨房用电功率、洗衣服用电功率、热水器用电功率
path1='datas/household_power_consumption_1000.txt'
df = pd.read_csv(path1, sep=';', low_memory=False)#没有混合类型的时候可以通过low_memory=F调用更多内存，加快效率）

df.head() ## 获取前五行数据查看查看

	Date	Time	Global_active_power	Global_reactive_power	Voltage	Global_intensity	Sub_metering_1	Sub_metering_2	Sub_metering_3
0	16/12/2006	17:24:00	4.216	0.418	234.84	18.4	0.0	1.0	17.0
1	16/12/2006	17:25:00	5.360	0.436	233.63	23.0	0.0	1.0	16.0
2	16/12/2006	17:26:00	5.374	0.498	233.29	23.0	0.0	2.0	17.0
3	16/12/2006	17:27:00	5.388	0.502	233.74	23.0	0.0	1.0	17.0
4	16/12/2006	17:28:00	3.666	0.528	235.68	15.8	0.0	1.0	17.0

# 查看格式信息
df.info()

RangeIndex: 1000 entries, 0 to 999
Data columns (total 9 columns):
Date                     1000 non-null object
Time                     1000 non-null object
Global_active_power      1000 non-null float64
Global_reactive_power    1000 non-null float64
Voltage                  1000 non-null float64
Global_intensity         1000 non-null float64
Sub_metering_1           1000 non-null float64
Sub_metering_2           1000 non-null float64
Sub_metering_3           1000 non-null float64
dtypes: float64(7), object(2)
memory usage: 70.4+ KB

# 异常数据处理(异常数据过滤)
new_df = df.replace('?', np.nan)#替换非法字符为np.nan
datas = new_df.dropna(axis=0, how = 'any') # 只要有一个数据为空，就进行行删除操作
datas.describe().T#观察数据的多种统计指标(只能看数值型的)

	count	mean	std	min	25%	50%	75%	max
Global_active_power	1000.0	2.418772	1.239979	0.206	1.806	2.414	3.308	7.706
Global_reactive_power	1000.0	0.089232	0.088088	0.000	0.000	0.072	0.126	0.528
Voltage	1000.0	240.035790	4.084420	230.980	236.940	240.650	243.295	249.370
Global_intensity	1000.0	10.351000	5.122214	0.800	8.400	10.000	14.000	33.200
Sub_metering_1	1000.0	0.000000	0.000000	0.000	0.000	0.000	0.000	0.000
Sub_metering_2	1000.0	2.749000	8.104053	0.000	0.000	0.000	1.000	38.000
Sub_metering_3	1000.0	5.756000	8.066941	0.000	0.000	0.000	17.000	19.000

# 查看格式信息
df.info()

RangeIndex: 1000 entries, 0 to 999
Data columns (total 9 columns):
Date                     1000 non-null object
Time                     1000 non-null object
Global_active_power      1000 non-null float64
Global_reactive_power    1000 non-null float64
Voltage                  1000 non-null float64
Global_intensity         1000 non-null float64
Sub_metering_1           1000 non-null float64
Sub_metering_2           1000 non-null float64
Sub_metering_3           1000 non-null float64
dtypes: float64(7), object(2)
memory usage: 70.4+ KB

## 创建一个时间函数格式化字符串
def date_format(dt):
    # dt显示是一个series/tuple；dt[0]是date，dt[1]是time
    import time
    t = time.strptime(' '.join(dt), '%d/%m/%Y %H:%M:%S')
    return (t.tm_year, t.tm_mon, t.tm_mday, t.tm_hour, t.tm_min, t.tm_sec)

## 需求：构建时间和功率之间的映射关系，可以认为：特征属性为时间；目标属性为功率值。
# 获取x和y变量, 并将时间转换为数值型连续变量
X = datas.iloc[:,0:2]
X = X.apply(lambda x: pd.Series(date_format(x)), axis=1)
Y = datas['Global_active_power']

X.head(2)

	0	1	2	3	4	5
0	2006	12	16	17	24	0
1	2006	12	16	17	25	0

## 对数据集进行测试集合训练集划分
# X：特征矩阵(类型一般是DataFrame)
# Y：特征对应的Label标签(类型一般是Series)
# test_size: 对X/Y进行划分的时候，测试集合的数据占比, 是一个(0,1)之间的float类型的值
# random_state: 数据分割是基于随机器进行分割的，该参数给定随机数种子；给一个值(int类型)的作用就是保证每次分割所产生的数数据集是完全相同的
X_train,X_test,Y_train,Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)

print(X_train.shape)
print(X_test.shape)
print(Y_train.shape)

(800, 6)
(200, 6)
(800,)

# 查看训练集上的数据信息(X)
X_train.describe()

## 数据标准化
# StandardScaler：将数据转换为标准差为1的数据集(有一个数据的映射)
# scikit-learn中：如果一个API名字有fit，那么就有模型训练的含义，没法返回值
# scikit-learn中：如果一个API名字中有transform， 那么就表示对数据具有转换的含义操作
# scikit-learn中：如果一个API名字中有predict，那么就表示进行数据预测，会有一个预测结果输出
# scikit-learn中：如果一个API名字中既有fit又有transform的情况下，那就是两者的结合(先做fit，再做transform)
ss = StandardScaler() # 模型对象创建
X_train = ss.fit_transform(X_train) # 训练模型并转换训练集
X_test = ss.transform(X_test) ## 直接使用在模型构建数据上进行一个数据标准化操作 (测试集)

pd.DataFrame(X_train).describe()

	0	1	2	3	4	5
count	800.0	800.0	8.000000e+02	8.000000e+02	8.000000e+02	800.0
mean	0.0	0.0	2.445821e-15	-8.604228e-17	8.104628e-17	0.0
std	0.0	0.0	1.000626e+00	1.000626e+00	1.000626e+00	0.0
min	0.0	0.0	-1.221561e+00	-1.333814e+00	-1.722545e+00	0.0
25%	0.0	0.0	-1.221561e+00	-8.377420e-01	-8.532677e-01	0.0
50%	0.0	0.0	8.186245e-01	-3.416698e-01	1.600918e-02	0.0
75%	0.0	0.0	8.186245e-01	1.022529e+00	8.852861e-01	0.0
max	0.0	0.0	8.186245e-01	1.518601e+00	1.696611e+00	0.0

## 模型训练
lr = LinearRegression(fit_intercept=True) # 模型对象构建
lr.fit(X_train, Y_train) ## 训练模型
## 模型校验
y_predict = lr.predict(X_test) ## 预测结果

print("训练集上R2:",lr.score(X_train, Y_train))
print("测试集上R2:",lr.score(X_test, Y_test))
mse = np.average((y_predict-Y_test)**2)
rmse = np.sqrt(mse)
print("rmse:",rmse)

训练集上R2: 0.24409311805909026
测试集上R2: 0.12551628513735869
rmse: 1.1640923459736248

# 输出模型训练得到的相关参数
print("模型的系数(θ):", end="")
print(lr.coef_)
print("模型的截距:", end='')
print(lr.intercept_)

模型的系数(θ):[ 0.00000000e+00 -6.66133815e-16 -1.41588166e+00 -9.34953243e-01
 -1.02140756e-01  0.00000000e+00]
模型的截距:2.4454375000000033

## 模型保存/持久化
# 在机器学习部署的时候，实际上其中一种方式就是将模型进行输出；另外一种方式就是直接将预测结果输出
# 模型输出一般是将模型输出到磁盘文件
from sklearn.externals import joblib

# 保存模型要求给定的文件所在的文件夹必须存在
joblib.dump(ss, "result/data_ss.model") ## 将标准化模型保存
joblib.dump(lr, "result/data_lr.model") ## 将模型保存

# 加载模型
ss3 = joblib.load("result/data_ss.model") ## 加载模型
lr3 = joblib.load("result/data_lr.model") ## 加载模型

# 使用加载的模型进行预测
data1 = [[2006, 12, 17, 12, 25, 0]]
data1 = ss3.transform(data1)
print(data1)
lr3.predict(data1)

[[ 0.          0.          0.81862454  0.15440249 -0.27374978  0.        ]]



array([1.16996393])

## 预测值和实际值画图比较
t=np.arange(len(X_test))
plt.figure(facecolor='w')#建一个画布，facecolor是背景色
plt.plot(t, Y_test, 'r-', linewidth=2, label='真实值')
plt.plot(t, y_predict, 'g-', linewidth=2, label='预测值')
plt.legend(loc = 'upper left')#显示图例，设置图例的位置
plt.title("线性回归预测时间和功率之间的关系", fontsize=20)
plt.grid(b=True)#加网格
plt.show()

## 功率和电流之间的关系
X = datas.iloc[:,2:4]
Y2 = datas.iloc[:,5]

## 数据分割
X2_train,X2_test,Y2_train,Y2_test = train_test_split(X, Y2, test_size=0.2, random_state=0)

## 数据归一化
scaler2 = StandardScaler()
X2_train = scaler2.fit_transform(X2_train) # 训练并转换
X2_test = scaler2.transform(X2_test) ## 直接使用在模型构建数据上进行一个数据标准化操作 

## 模型训练
lr2 = LinearRegression()
lr2.fit(X2_train, Y2_train) ## 训练模型

## 结果预测
Y2_predict = lr2.predict(X2_test)

## 模型评估
print("电流预测准确率: ", lr2.score(X2_test,Y2_test))
print("电流参数:", lr2.coef_)

## 绘制图表
#### 电流关系
t=np.arange(len(X2_test))
plt.figure(facecolor='w')
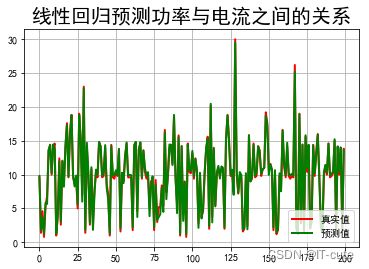
plt.plot(t, Y2_test, 'r-', linewidth=2, label=u'真实值')
plt.plot(t, Y2_predict, 'g-', linewidth=2, label=u'预测值')
plt.legend(loc = 'lower right')
plt.title(u"线性回归预测功率与电流之间的关系", fontsize=20)
plt.grid(b=True)
plt.show()

电流预测准确率:  0.9920420609708968
电流参数: [5.07744316 0.07191391]