【线段树】模板

一.简介

 线段树（Segment Tree）是一种用于解决区间查询问题的数据结构。它可以高效地支持区间查询和区间更新操作。

线段树的基本思想是将一个区间划分为多个子区间，并为每个子区间维护一些信息。这些信息可以是区间内元素的和、最大值、最小值等等，根据具体问题而定。

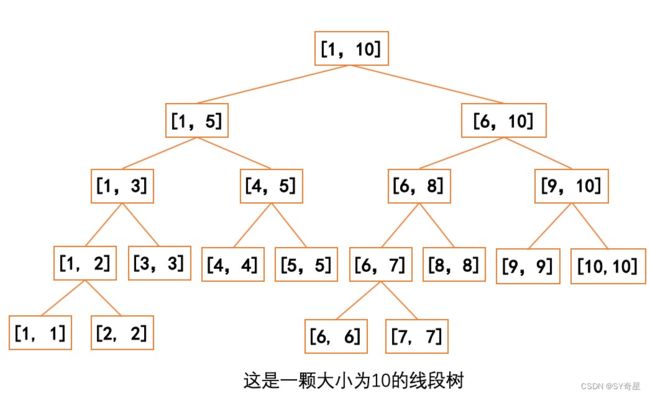
线段树的构建过程是一个递归的过程。首先将整个区间划分为两个子区间，然后递归地构建每个子区间的线段树，直到区间长度为1。构建过程中，每个节点都会保存其对应区间的信息。

线段树的查询操作也是一个递归的过程。根据查询的区间与当前节点的区间的关系，可以选择向左子节点或右子节点进行递归查询，直到找到与查询区间完全重叠的节点。

线段树的更新操作也是类似的递归过程。根据更新的位置与当前节点的区间的关系，可以选择向左子节点或右子节点进行递归更新，直到找到需要更新的位置。

线段树的时间复杂度为O(logN)，其中N是区间的长度。线段树在解决一些区间查询问题，如区间最值、区间和等问题上非常高效，被广泛应用于各种算法和数据结构中。

 

---

二.树的建立（维护区间和） 

#include
#define maxn 100005
using namespace std;
int n;
int a[maxn]; //原数组 
struct node{
	int l,r;
	int sum;
}tree[maxn<<2]; //注意要乘4

void build(int p,int l,int r) {
	tree[p].l=l; tree[p].r=r;
	if(l==r){
		tree[p].sum=a[l];
		return ;
	}
	int mid=(l+r)>>1;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	tree[p].sum=tree[p<<1].sum+tree[p<<1|1].sum; //回溯的过程中维护父节点的sum 
}
int main(){
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build(1,1,n);
	cout<

---

三.区间和的查询

#include
#define maxn 100005
using namespace std;
int n;
int a[maxn]; //原数组 
struct node{
	int l,r;
	int sum;
}tree[maxn<<2]; //注意要乘4

void build(int p,int l,int r) {
	tree[p].l=l; tree[p].r=r;
	if(l==r){
		tree[p].sum=a[l];
		return ;
	}
	int mid=(l+r)>>1;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	tree[p].sum=tree[p<<1].sum+tree[p<<1|1].sum; //回溯的过程中维护父节点的sum 
}

int ask(int p,int l,int r){
	if(l<=tree[p].l && r>=tree[p].r) return tree[p].sum;
	int mid=(tree[p].l+tree[p].r)>>1;
	int ans=0;
	if(l<=mid) ans+=ask(p<<1,l,r);
	if(r>mid) ans+=ask(p<<1|1,l,r);
	return ans;
}
int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build(1,1,n);
	while(m--){
		int l,r;
		scanf("%d%d",&l,&r);
		cout<

---

四.修改

#include
#define maxn 100005
using namespace std;
int n;
int a[maxn]; //原数组 
struct node{
	int l,r;
	int sum;
}tree[maxn<<2]; //注意要乘4

void build(int p,int l,int r) {
	tree[p].l=l; tree[p].r=r;
	if(l==r){
		tree[p].sum=a[l];
		return ;
	}
	int mid=(l+r)>>1;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	tree[p].sum=tree[p<<1].sum+tree[p<<1|1].sum; //回溯的过程中维护父节点的sum 
}

int ask(int p,int l,int r){
	if(l<=tree[p].l && r>=tree[p].r) return tree[p].sum;
	int mid=(tree[p].l+tree[p].r)>>1;
	int ans=0;
	if(l<=mid) ans+=ask(p<<1,l,r);
	if(r>mid) ans+=ask(p<<1|1,l,r);
	return ans;
}

void change(int p,int l,int r,int w){
	if(l<=tree[p].l && r>=tree[p].r){
		tree[p].sum+=w*(tree[p].r-tree[p].l+1);
		return;
	}
	int mid=(tree[p].l+tree[p].r)>>1;
	if(l<=mid) change(p<<1,l,r,w);
	if(r>mid) change(p<<1|1,l,r,w);
	tree[p].sum=tree[p<<1].sum+tree[p<<1|1].sum;
}

int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build(1,1,n);
	while(m--){
		int op,l,r,w;
		scanf("%d",&op);
		if(op==1){
			scanf("%d%d%d",&l,&r,&w);
			change(1,l,r,w);
		}else{
			scanf("%d%d",&l,&r);
			cout<

---

五.懒惰标记

#include
#define maxn 100005
using namespace std;
typedef long long ll;
int n;
int a[maxn]; //原数组 
struct node{
	int l,r;
	ll sum;
	int add; //懒惰标记 
}tree[maxn<<2]; //注意要乘4

void build(int p,int l,int r) {
	tree[p].l=l; tree[p].r=r;
	if(l==r){
		tree[p].sum=a[l];
		return ;
	}
	int mid=(l+r)>>1;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	tree[p].sum=tree[p<<1].sum+tree[p<<1|1].sum; //回溯的过程中维护父节点的sum 
}
void push_up(int p){
	if(tree[p].add){
		tree[p<<1].sum+=tree[p].add*(tree[p<<1].r-tree[p<<1].l+1);
		tree[p<<1|1].sum+=tree[p].add*(tree[p<<1|1].r-tree[p<<1|1].l+1);
		tree[p<<1].add+=tree[p].add;
		tree[p<<1|1].add+=tree[p].add;
		tree[p].add=0;
	}
}
ll ask(int p,int l,int r){
	if(l<=tree[p].l && r>=tree[p].r) return tree[p].sum;
	push_up(p); //把没传完的懒惰值传一下 
	int mid=(tree[p].l+tree[p].r)>>1;
	ll ans=0;
	if(l<=mid) ans+=ask(p<<1,l,r);
	if(r>mid) ans+=ask(p<<1|1,l,r);
	return ans;
}

void change(int p,int l,int r,int w){
	if(l<=tree[p].l && r>=tree[p].r){
		tree[p].sum+=(ll)w*(tree[p].r-tree[p].l+1); //只维护了一个，相关联的节点也要维护 
		tree[p].add+=w;  //先标记一下，攒在一起，到时候一起传 
		return;
	}
	push_up(p);  //该传了 
	int mid=(tree[p].l+tree[p].r)>>1;
	if(l<=mid) change(p<<1,l,r,w);
	if(r>mid) change(p<<1|1,l,r,w);
	tree[p].sum=tree[p<<1].sum+tree[p<<1|1].sum;
}

int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build(1,1,n);
	while(m--){
		int op,l,r,w;
		scanf("%d",&op);
		if(op==1){
			scanf("%d%d%d",&l,&r,&w);
			change(1,l,r,w);
		}else{
			scanf("%d%d",&l,&r);
			cout<

---

六.模板题

P3372 【模板】线段树 1 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

---

七.参考代码

注意：不开long long见祖宗！

#include
#define maxn 100005
using namespace std;
typedef long long ll;
int n;
int a[maxn]; //原数组 
struct node{
	int l,r;
	ll sum;
	int add; //懒惰标记 
}tree[maxn<<2]; //注意要乘4

void build(int p,int l,int r) {
	tree[p].l=l; tree[p].r=r;
	if(l==r){
		tree[p].sum=a[l];
		return ;
	}
	int mid=(l+r)>>1;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	tree[p].sum=tree[p<<1].sum+tree[p<<1|1].sum; //回溯的过程中维护父节点的sum 
}
void push_up(int p){
	if(tree[p].add){
		tree[p<<1].sum+=tree[p].add*(tree[p<<1].r-tree[p<<1].l+1);
		tree[p<<1|1].sum+=tree[p].add*(tree[p<<1|1].r-tree[p<<1|1].l+1);
		tree[p<<1].add+=tree[p].add; //儿子也有惰性 
		tree[p<<1|1].add+=tree[p].add;
		tree[p].add=0;  //记得清0 
	}
}
ll ask(int p,int l,int r){
	if(l<=tree[p].l && r>=tree[p].r) return tree[p].sum;
	push_up(p); //把没传完的懒惰值传一下 
	int mid=(tree[p].l+tree[p].r)>>1;
	ll ans=0;
	if(l<=mid) ans+=ask(p<<1,l,r);
	if(r>mid) ans+=ask(p<<1|1,l,r);
	return ans;
}

void change(int p,int l,int r,int w){
	if(l<=tree[p].l && r>=tree[p].r){
		tree[p].sum+=(ll)w*(tree[p].r-tree[p].l+1); //只维护了一个，相关联的节点也要维护 
		tree[p].add+=w;  //先标记一下，攒在一起，到时候一起传 
		return;
	}
	push_up(p);  //该传了 
	int mid=(tree[p].l+tree[p].r)>>1;
	if(l<=mid) change(p<<1,l,r,w);
	if(r>mid) change(p<<1|1,l,r,w);
	tree[p].sum=tree[p<<1].sum+tree[p<<1|1].sum;  //维护父节点 
}

int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build(1,1,n);
	while(m--){
		int op,l,r,w;
		scanf("%d",&op);
		if(op==1){
			scanf("%d%d%d",&l,&r,&w);
			change(1,l,r,w);
		}else{
			scanf("%d%d",&l,&r);
			cout<