排序(二):归并排序,快速排序,堆排序
归并排序
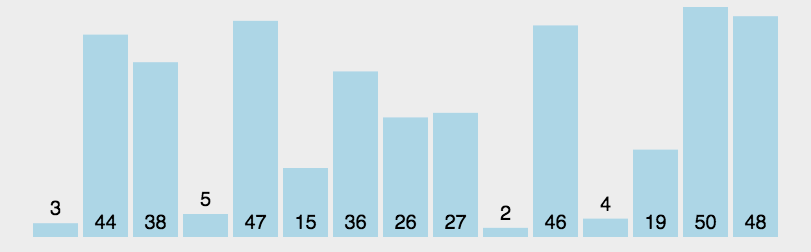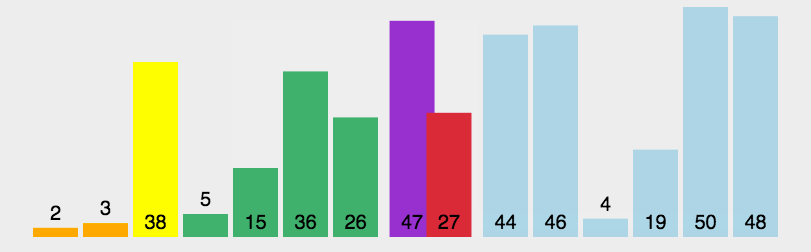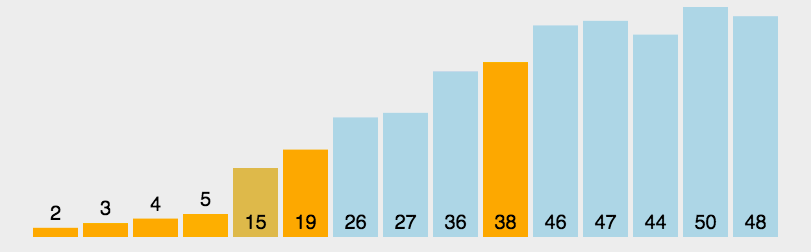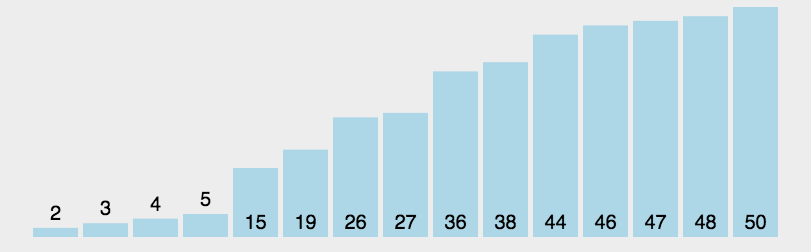
归并排序是基于“归并”思想的排序方法,利用two pointers思想。这里说的是二路归并,就是将两个小集合归并为一个大集合,依次类推,当然要将集合合并,但给我们的只有一个集合,所以要先划分成n/2个个数为2的集合,动图演示在最下方。
方法一:递归实现,这个方法其实很简单,就反复将当前的区间[left,right]分为两半,对两个子区间[left,mid],[mid+1,right]分别递归进行归并排序,然后合并两个序列即可。
代码(递归实现)
#include性能分析:空间复杂度为O(n),时间复杂度为O(nlogn),稳定的排序。
快速排序
快速排序也利用了two pointers(双指针)的思想。
1.将第一个元素作为基准,找到一个位置,使得第一个元素的左边不超过基准,右边不小于基准。
2.对元素的左侧和右侧分别递归重复进行1操作,直到当前调整区间的长度不超过1。
注意,当序列是有序的时候,使用快排的时间复杂度将降为O(n²)。改进的方法有很多,这里只说一下三数取中法。
代码
#include性能分析:空间复杂度为O(logn),时间复杂度为O(nlogn),不稳定的排序。
堆排序
首先来浅谈一下堆的概念,堆是一个完全二叉树,其有大根堆和小根堆之分。大根堆就是根节点比它的左子树和右子树都大,小根堆就是根节点比它的左子树和右子树都小。这里我采用的是大根堆,方法是向下调整的方法,所谓向下调整就是让调整的某点依次向下比较,选取左子树和右子树中最大的那个,与其交换后在向下调整,直至没有左子树或右子树或者子树没有比它更大的数。怎样建堆是关键,我们不需要遍历整个数,只需遍历到n/2到0即可,因为n/2要么是最后一层,要么是倒数第二层。
最后就是排序了,排序的方法就是依次将树的根节点和最后一个节点交换后,然后对[0,n-1]向下取整。动画演示
代码
#include